AtCoder Beginner Contest 140 E - Second Sum

お題箱より。

解法

まずは「数え上げの順番をひっくり返す」という発想が大事です。

をひっくり返して、

と言い換えることで見通しが良くなります。

ではある要素 $P_{i}$ が2番手になる条件を考えると、それは「自分より大きい要素がちょうど1つだけ存在する」ということなので、以下のように考えることができます。

f:id:betrue12:20200328121523p:plain

$P_{i}$ として見ている要素より大きいものだけを見て、左隣2個と右隣2個がどこにあるのか分かれば、図のように境界線を考えることで

の合計によって $P_{i}$ が2番手となるような区間を数えることができます。ただし図の右側のように2個以上の要素が存在しない場合は一番端を境界として扱います。

これは $P_{i}$ を値として大きい方から見ていきながら、そのインデックスをデータ構造に入れていき、その中で左隣2つと右隣2つを探せば良いです。2通りの実現方法を紹介します。

C++であれば順序付き集合として二分探索や隣の要素の取得ができる set を使うのが便利です。いったん $P_{i}$ を入れたあと、lower_bound等でそのイテレータを取得し、prev と next を用いて隣の要素を取得すれば良いです。

2個隣の要素が存在しない場合は範囲外アクセスになってしまうので、場合分けをするか、「一番端」に上手く対応するような要素を番兵として入れておくと良いです。

順序付き集合がない場合はこちらで。各インデックスに要素があれば $1$ 、要素がなければ $0$ という状態をBITで管理し、区間和と二分探索で「隣の要素」を特定します。

f:id:betrue12:20200328122840p:plain

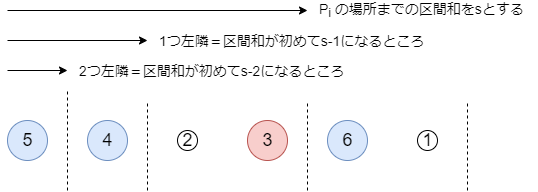
BIT上の二分探索は普通に実装すると、二分探索のループとBITのアクセスで $O((\log N)^{2})$ かかります。上手く実装すれば $O(\log N)$ にもできますが、PyPyであれば $O((\log N)^{2})$ でも通りました。