AtCoder Beginner Contest 143 F - Distinct Numbers
解法
色々な解法があるみたいですが…この記事ではそれぞれの について独立に解きます。ある
について解くときには、可能な操作回数には単調性があるので二分探索できます。
ある と操作回数
を固定したときに、操作を
回行えるかどうか判定する方法を考えます。まず
は必ず満たす必要があります。その上で
の中から使う整数を
個選んで
(*) 全部で 個の整数から、「異なる
個の整数を取り除く」という操作を
回行うことができる
かどうかを判定したいです。このとき(*)の必要十分条件として、
全ての整数値 について、
個の中に
が含まれる個数は
個以下である
というものがあります。
必要性については、もし 個を超える整数値が存在する場合はそれらを
回の操作で全て取り除くことができないことから示せます。
十分性については、以下のようにすると実際に構成できることから示せます。(Special Thanks:てんぷらさん)
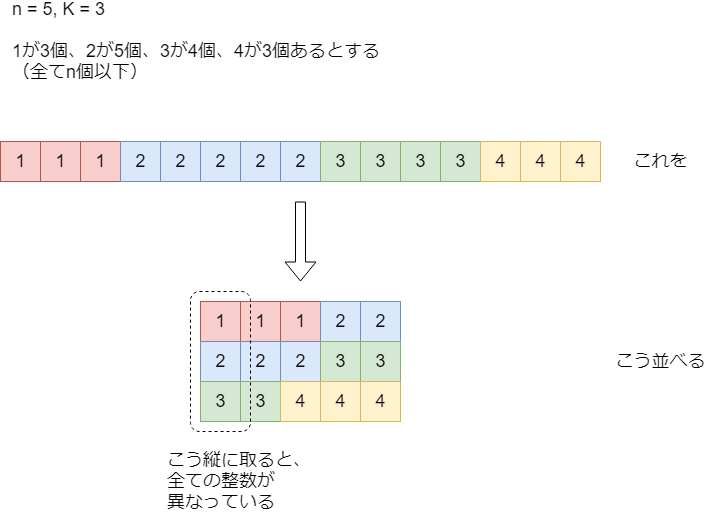
つまり から各整数値を
個以下取ってきて、合計で
個確保できればOKということになります。これは以下のように解くことが出来ます。
まず を「整数値○が
個、整数値△が
個…」という風に集計したときの数列
を求めて、これをソートしておきます。このとき各整数値を
個以下取ろうとすると、
であるような
については全て取る。
であるような
についてはそれぞれ
個ずつ取る。
ということになります。1.と2.の境界を二分探索などで求めて、1.については累積和を求めておくと、取れる個数の合計を効率的に求めることが出来ます。これが 以上かどうか判定すれば良いです。
この解法だと全ての を試すので
、答えを求めるための二分探索で
、
を満たす境界を求めるのに
で、全体
になります。ちょっと重いですね。
を満たす境界を全ての
について前計算しておくと
が1個落ちるなど、計算量の改善は色々あると思います。