お題箱より。
解法
公式解説と逆になってしまいますが、与えられる を改めて
と定義します。これが正である頂点は「過剰なので減らす必要がある」、負である頂点は「不足しているので増やす必要がある」ことになり、全ての
を
にするのが目標です。
適当に根を決め、木DPのように葉から操作していきます。実装方法は何通りかありそうですが、私の場合は以下のようにしました。
頂点 を操作する時には、
- 頂点
の子孫である（頂点
については、全て
となっている。
- 頂点
となっている。
という条件が満たされるまで操作をすることにします。具体的にどういう操作になるのか考えましょう。
まず頂点 の直接の子である頂点
は
となっている可能性があるので、まずこれを
にする必要があります。子の不足分の最大値と同じ回数だけ頂点
を操作します。
このとき、不足分が最大である子以外には余分に値を送ってしまうので、それを「押し返す」必要があります。この押し返しにかかるコストは後で計算します。
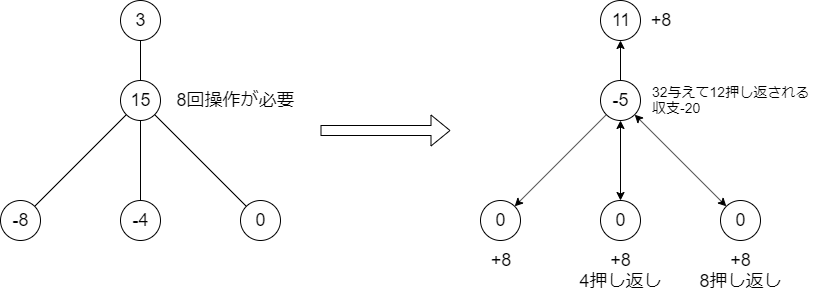
直接の子全てについて となったら、その時点での
の値を確認します。これが正でなければこれで終わりですが、もし正であればさらにこれを親側に押し出す操作をします。このときやはり子には余分に値を送ってしまうので、「押し返し」が発生します。
押し返しのコストについて考えましょう。頂点 の親から余分に値
が送られた時に、頂点
より下の値を変えずにその
を親側に送り返すためにかかる合計操作回数を
とします。これは頂点
を操作する
回と、頂点
の全ての子
に入ってしまう
をさらに押し返すための
の合計として計算できます。
これを根まで続けると、「必ず目的を達成できる」という制約から根 についてちょうど
となり、それまでの全ての操作回数の合計として答えが求められます。