AtCoder Grand Contest 034 E - Complete Compress

公式解説とちょっと違う方法で通したので書いておきます。

解法

木DPを考える

コマを集める頂点を全て試すことにします。集める頂点を $r$ と表記し、 $r$ を根とする木DPを考えます。

それぞれの頂点 $i$ について、それ以下にある部分木に含まれるコマは必ず頂点 $i$ を通ります。そこで「ある頂点 $i$ 以下の部分木にあるコマを全て頂点 $i$ に集めるために、部分木の外にあるコマと行う操作の回数」を考え、これを単に「外との操作回数」と呼ぶことにします。問題の条件を満たす動かし方は、根について外との操作回数が0回になるような動かし方と言うことができます。

そこで各頂点について以下のような値を計算する木DPを考えてみましょう。

$dp\lbrack i \rbrack =$ 頂点 $i$ 以下の部分木にあるコマを全て頂点 $i$ に集めるために、部分木の外にあるコマとの操作を最小で何回行う必要があるか。

つまり外との操作回数の最小値です。これが $dp\lbrack r \rbrack = 0$ となれば目的達成です。

遷移を考える

次にこのDPの遷移を考えましょう。

ある頂点 $j$ について $dp\lbrack j \rbrack$ が求められているとします。それらのコマを親 $i$ に動かすためには、それぞれのコマについてさらに1回ずつの操作が必要になります。つまり頂点 $j$ 以下の部分木に含まれるコマの個数を $n\lbrack j \rbrack$ として $dp\lbrack j \rbrack + n\lbrack j \rbrack$ 回の操作が必要です。

頂点 $i$ について外との操作回数を最小にするためには、それぞれの子について必要な操作回数を集めて、違う子同士で可能な限り相殺して…と考えたいところですが、それぞれの部分木で可能な限り相殺して外との操作回数を小さくしてしまうと後で困るケースがあります。例えば以下のようなケースです。

f:id:betrue12:20190605015220p:plain

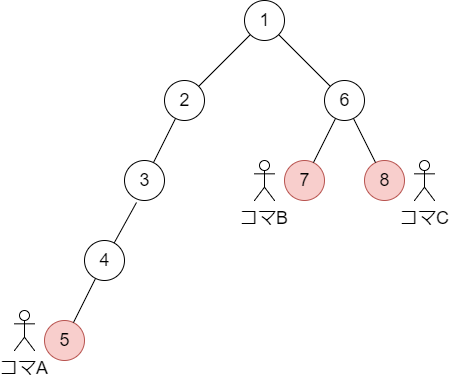
このケースは頂点1に全コマを集めることが可能ですが、貪欲に相殺して頂点6を見る段階でコマBとCを操作してしまうとアウトです。正解はコマAとBの操作、コマAとCの操作を2回ずつ行うことです。

このようなケースはどのように考慮するべきでしょうか。愚直解法としては、最小値だけでなく外との操作回数として取りうる値を全て持っておく…というものが考えられますが、実は取りうる値の最小値と最大値を持っておくことで解決します。この最大値は「部分木で一切の相殺をしない」という場合に相当するので、すなわち部分木内の各コマと頂点 $i$ との距離の和になります。

このことについて細かく見ていき、遷移を詰めていきましょう。

遷移を細かく考察する

まず、頂点 $i$ それぞれについて外との操作回数は必ず偶数・奇数どちらかになります。これは外との操作回数が、その最大値から部分木内だけで操作された回数の2倍を引いたものであることから分かります。

そして操作回数の最小値と最大値の間にある値は、偶奇が一致していれば必ずそれらの値を実現する操作が可能です。これは最小値を実現する操作から、部分木内で行っている操作を1組ずつ解消していくと考えれば良いです。

この性質を利用してDPの遷移を考えましょう。頂点 $i$ についての外との操作回数の最小値と最大値を子たちの情報から求めます。最大値は先述の通り各コマと頂点 $i$ との距離和として単純に計算できるので、考えるべきは最小値です。

子が1つしかないときは相殺できないので明らかです。複数の子がある場合、イメージとしては必要操作回数がまんべんなく散らばっていると相殺できて最小値は小さくできます。逆に1つの子だけに操作回数が偏っていると相殺しきれない分が増えます。

f:id:betrue12:20190605020233p:plain

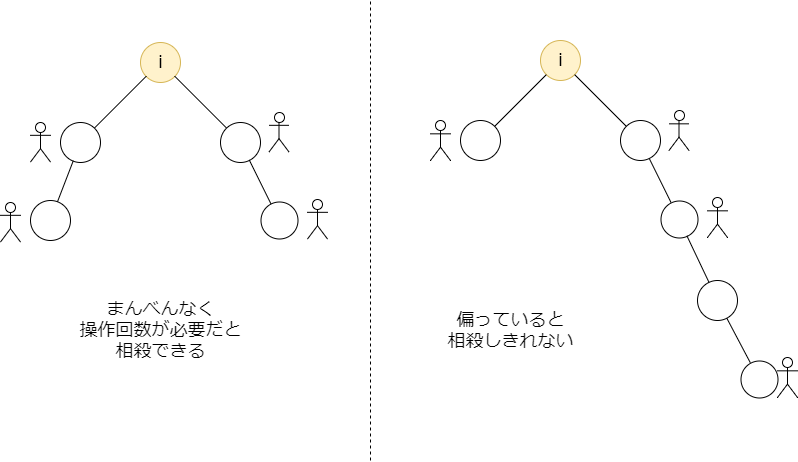
これを具体的に式で書いていきましょう。子 $j$ についての外との操作回数の最大値を $dp_{\max}\lbrack j \rbrack$ とし、先程まで $dp\lbrack j \rbrack$ としていた最小値を改めて $dp_{\min}\lbrack j \rbrack$ とします。先程と同じく頂点 $j$ 以下の部分木に含まれるコマの個数を $n\lbrack j \rbrack$ とします。

頂点 $i$ の子全ての集合を $J$ とします。このとき、 $dp_{\min}\lbrack i \rbrack$ は以下のように計算することができます。

$\displaystyle dp_{\min}\lbrack i \rbrack = \max_{k\in J}\lbrace (dp_{\min}\lbrack k \rbrack + n\lbrack k \rbrack) - \sum_{j\in J, j\ne k} (dp_{\max}\lbrack j \rbrack + n\lbrack j \rbrack) \rbrace$

※ただしこの値が負になる場合は、偶数なら0、奇数なら1。

つまり $k$ が「操作回数を相殺しきれないかもしれない子」の候補で、これを全部試します。 $k$ の操作回数を最小に、他の子の操作回数を最大にしたときに、相殺しきれないぶんがあればそれは頂点 $i$ のさらに外との操作で補わないといけません。これを全ての $k$ について試した最大値が $dp_{\min}\lbrack i \rbrack$ となります。

もちろん負にはなれないのでそこは考慮します。計算結果が負になったときに偶数なら0、奇数なら1を実現する操作が必ず存在することは、それぞれの子について先程の「操作回数の最小値の最大値の間にある値は、偶奇が一致していれば必ずそれらの値を実現する操作が可能」という性質が成り立っていることから言えます。

これで遷移ができました。先程の $\displaystyle dp_{\min}\lbrack i \rbrack$ の計算は、 $\sum_{j\in J, j\ne k}$ の部分については全部の合計を計算しておいて1個引けばよいので、子の個数についての線形時間で計算できます。つまり木DPが全体で $O(N)$ になり、根を全部試しても全体 $O(N^{2})$ で間に合います。

付録：逆走について

これは公式解説でも触れられていますが、コマを集める頂点 $r$ を決めた時に、その頂点から一方のコマが遠ざかるような操作（逆走）はしても得がないことは確かめておく必要があります。ここまでの解法では逆走については一切考慮していませんでした。

f:id:betrue12:20190605020451p:plain

不必要に逆走すると操作回数は増えるので明らかに損です。もし仮に「逆走なしで考えると不可能だけど、あえて逆走することで条件を満たす操作が可能になる」という可能性があれば逆走を考慮する必要がありますが、そのようなこともありません。それを（厳密ではないですが）軽く説明します。

もし頂点 $i$ のある子 $j$ について、 $j$ 以下の部分木の中で逆走をしてみたとします。このときその2つのコマは、片方は頂点 $i$ から遠ざかり片方は近づくので、 $i$ との距離和は変化しません。つまり部分木の外と行う必要がある操作回数も同じです。そのためもし逆走を含む操作で条件を満たせるならば、外との操作を行うコマを適切に入れ替えることで逆走なしで条件を満たせるはずです。

このことから、あえて逆走することに得はないことが分かります。