ARMERIA

Rubyと競技プログラミングの話　AtCoderやCodeforcesの問題解説記事が多め。

AISing Programming Contest 2019 参加記録＆解説

AtCoder プログラミング 競技プログラミング

AISing Programming Contest 2019 - AtCoder

全完！

2000未満ratedコンテストだったのでパフォーマンスは付かず、ちょっと残念。

f:id:betrue12:20190112235728p:plain

A - Bulletin Board

A - Bulletin Board

解法

縦の位置が N-H+1 通り、横の位置が N-W+1 通りあるので、これらを掛け算したものが答えです。

ACコード

B - Contests

B - Contests

解法

「1問目になるもの」「2問目になるもの」「3問目になるもの」がそれぞれ排他、つまり点数の範囲が被っていないことが重要です。それぞれの問題数を数えて、一番小さいものを出力すればよいです。

ACコード

C - Alternating Path

C - Alternating Path

解法

黒→白→黒→白…と移動することは、「今いるマスと違う色のマスに移動する」ことと考えることができます。そう考えると、違う色で隣り合っているマスは「相互に行き来できるマス」ということになります。

この相互に行き来できるマス同士を繋いでいくと、グリッドの中で「この範囲内はどのマスからどのマスへも相互に行き来できる」という領域ができます。そうするとこの領域内の黒のマス数×白のマス数だけ、問題の条件を満たすペアを作ることができます。これを領域ごとに数えて全部足すと答えになります。

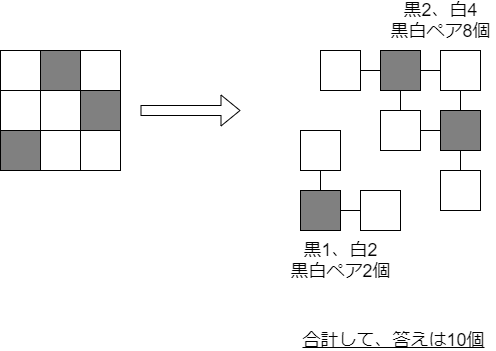
f:id:betrue12:20190113152616p:plain

あとは「領域の調べ方、数え方」ですが、これは幅優先探索/深さ優先探索などが楽だと思います。あるマスから始めて、違う色で隣り合っている未訪問のマスを探索していけばよいです。

ACコード

D - Nearest Card Game

D - Nearest Card Game

解法

ここから難易度が上がるので、解説もしっかりしていきたいと思います…

二人が取るカードの全体像を掴む

たくさんの x の値について答えを出さなくてはいけませんが、まずは一旦それを忘れて、ある1つの x について考えます。

問題の操作から、高橋くんと青木くんがどのようにカードを取っていくか考えてみます。

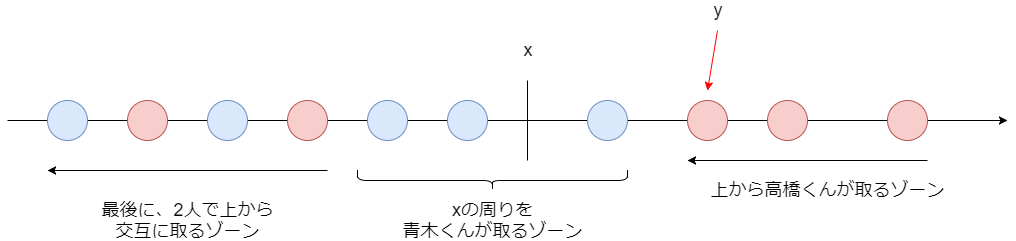
f:id:betrue12:20190113011859p:plain

全体の形としてはこのようになります。まず高橋くんは大きいほうから、青木くんは x の周りからカードを取っていきます。こうするといずれ高橋くんが青木くんの取っていた領域に当たってしまうので（図中の y のあたり）、その後は2人で交互に残った下の方のカードを大きい方から取っていきます。

もちろん、このうちどこかの領域は要素数がゼロかもしれません。例えば x がものすごく大きいところにある場合、2人は単に一番上から交互にカードを取っていくだけになります。

「境界」を探す

これらのゾーンの境界が知りたくなります。境界が分かってしまえば、累積和を用いて高橋くんのカードの合計が分かりそうです。

x より上にあるカードについて、そのカードを高橋くんと青木くんどちらが取るのか？を考えます。これを知るには、高橋くんと青木くんそれぞれについて「その人がそのカードを取るとしたら、何枚目に取るか？」を考えればよいです。

取る順番が早いほうがそのカードを取ります。同順の場合は先攻の高橋くんが取ります。

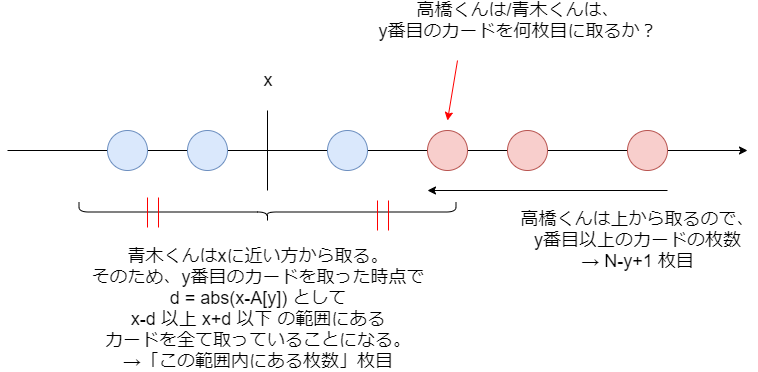
f:id:betrue12:20210118032906p:plain

高橋くんのほうは簡単で、一番上から取っていくので「そのカード以上にあるカードの枚数」がそのまま使えます。

青木くんのほうは少しだけ厄介ですが、 x に近いところから取る、距離が同じ場合は小さい方を先に取る、という条件から、カード y を取る時点で青木くんは、 d = |x-A_{y}| として x - d 以上 x+d 以下の範囲にあるカードを全て取っているはずです。なのでその範囲にあるカードの枚数を数えればよくて、ある座標範囲内にあるカードの枚数は二分探索などで求めることができます。

こうやって x より上側のカードについて「どちらが取るか」を判定できるので、これが逆転するところがさきほど示したゾーンの境界になります。

大量クエリの高速処理を考える

これで答えを求めるための道筋は見えました。あとは計算量です。

答えを求めなければいけない x がたくさんあるので、結局は「 x が与えられたときに高速にゾーンの境界を求められるか？」という話になります。これを解決する方法は2つあります。

  1. x の値が数直線の右側に移動すると、ゾーンの境界も右側に移動していくこと（単調性）を利用する。与えられた x をソートし、しゃくとり法で境界を求めていく。
  2. さきほどの「どちらが取るか」自体に単調性があることを利用し、これを二分探索する。

これはどちらでも良いです。計算量オーダーとして優位なのはしゃくとり法ですが、各クエリを独立に処理できたほうが分かりやすいので計算時間に余裕があれば二分探索でも良いでしょう。

境界が分かった後は、各ゾーンの累積和で答えを求めます。交互に取るゾーンがあるところも考慮し、1つ飛ばしの累積和（添字の偶奇ごとに累積和を取ったもの）も求めておくと良いです。

ACコード

E - Attack to a Tree

E - Attack to a Tree

解法

木DPの着想を得る

ある適当な点を根とする根付き木とみなし、葉から順番に値を計算していく木DPを考えてみます。

DPテーブルが持つ情報として必要そうなものは、「その頂点以下で何本の辺を切ったか」「その頂点を含む連結成分の、現時点での電力合計」です。このうち電力合計はとても大きい値になり得ますが、切った辺の本数は最大でもその頂点以下にある辺の本数なので比較的少ないです。そこで

  • dp\lbrack i \rbrack\lbrack j \rbrack ＝ 頂点 i 以下の部分木を考えたときに、辺を既に j 本切っているときの、頂点 i を含む連結成分の電力合計の最小値。ただし、辺を切ったことで既に確定している連結成分は問題の条件を満たしていなければならない。

と定義します。電力を足りなくさせることが目的、つまり電力合計をなるべく小さくしたいので最小値を取っています。

ただしこのままでは情報が不足しています。各連結成分が満たすべき条件は、「連結成分にコンピュータが存在しない」「連結成分内の電力合計が負」のどちらかなので、電力合計だけでなくコンピュータが存在するかどうかの情報が必要になってきます。そのため、

  • dp\lbrack i \rbrack\lbrack j \rbrack\lbrack k \rbrack ＝ 頂点 i 以下の部分木を考えたときに、辺を既に j 本切っていて、部分木内にコンピュータが存在する（ k=1）/しない（ k=0）ときの、頂点 i を含む連結成分の電力合計の最小値。ただし、辺を切ることで既に確定している連結成分は問題の条件を満たしていなければならない。

と各頂点が持つ値を定義します。以下はある状態において、各添字がどのようになるかを示す一例です。

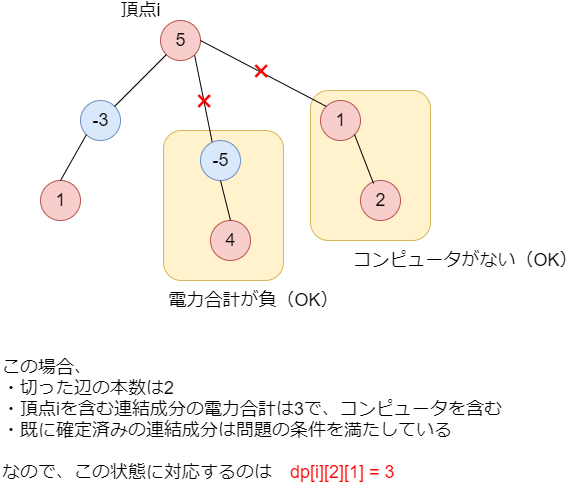
f:id:betrue12:20190113160918p:plain

これなら、後に示すように遷移を構成することができます。

遷移を考える

子の情報から親の情報へ、どのようにDPの遷移を作ればよいか考えてみます。

イメージとしては、最初は親を要素数1の部分木として考え、そこに子の部分木を1つずつマージしていきます。親と子それぞれについて、さきほどの j, k についてループを回します。

このとき、子からの辺を繋ぐか切るかという2通りが考えられます。

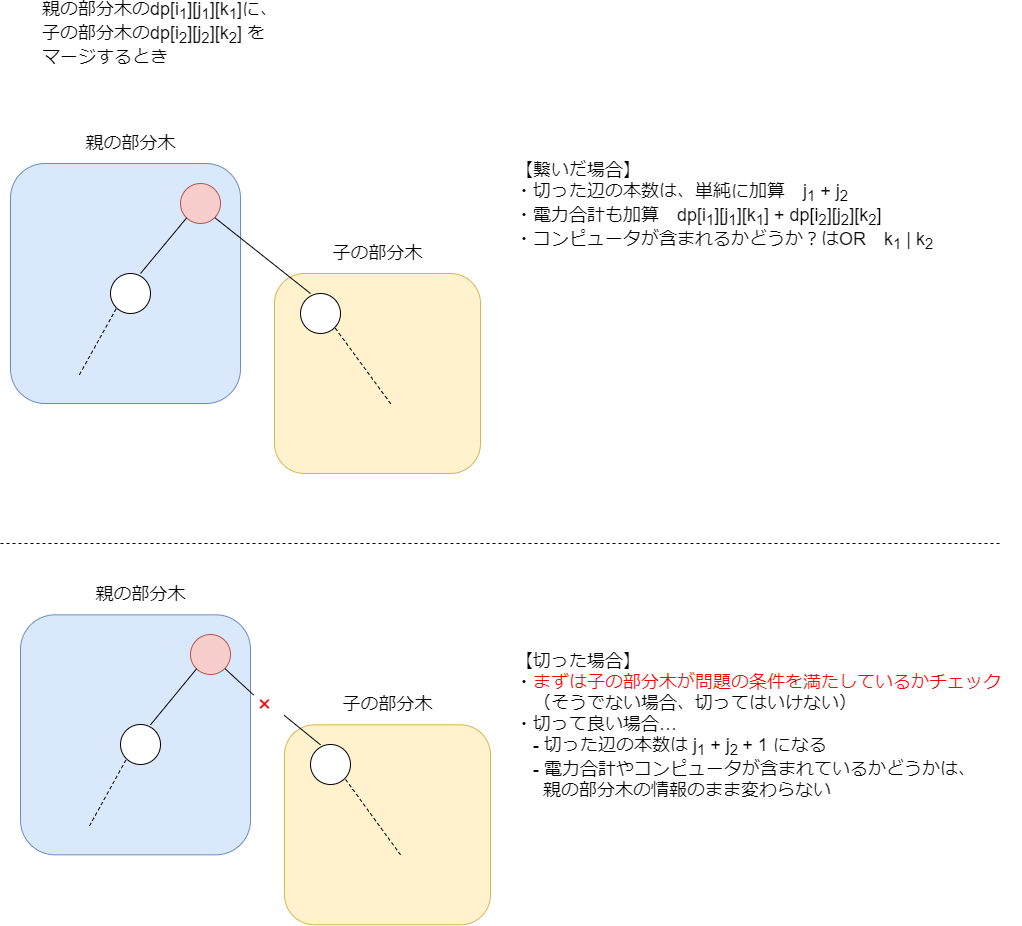
f:id:betrue12:20190113023514p:plain

添字が多いので式がややこしくなりがちですが、

  • 辺を繋ぐ場合、今までに切った辺の数・電力合計は加算し、コンピュータがあるかどうかはOR演算する。
  • 辺を繋がない場合、まずは子の部分木が条件を満たしているかどうかをチェック！ 満たしている場合は、切った辺の数は合計に1を足したものになり、それ以外の情報は親の情報がそのまま残る。

という風に遷移先を求めることができます。この遷移先に対して「今の値より値が小さくなるなら更新」と操作することを繰り返すと遷移ができます。

計算量について、通称「二乗の木DP」

さきほどのDP、子をマージするたびに親子それぞれの切った辺の数についてループを回すので計算量がひどくなりそうな気がします。具体的には全頂点について辺の数の2乗ループを回しているので、全体 O(N^{3}) になりそうです。

ですが、「その時点で持っている部分木のサイズまでしかループを回さない」という実装をすることで、全体計算量を O(N^{2}) とすることができます。これが通称「二乗の木DP」 と呼ばれるものです。部分木の辺の数は頂点の数-1なので、切った辺の数でループする場合はこのテクニックが使えます。

ACコード（＆実装について）

私の実装について少し補足です。

DPテーブルに持つ値についてですが、 INF という値を使っています。先ほど書いたようにこのテーブルの中には添字で定義された状態における電力合計の最小値が入っていますが、ときには「そのような添字に対応する状態が存在できない」ということがあります。一番単純な例では、部分木内にコンピュータが1つもない場合は dp\lbrack i \rbrack\lbrack j \rbrack\lbrack 1 \rbrack に対応する状態はありません。このようなときには値に INF を入れています。

この問題ではDPを回した後、最後に「辺の切り方が合計 j 本であるような、問題文の条件を満たす分け方が存在するか」を根について調べて、一番小さい切断本数を答えることになります。このときに「 INF の場合はそのような状態が存在しない」という決めごとをしておくと判定を正しく行うことができます。コードでは以下の部分です。

for(int n=0; n<N; n++){
    if(dp[0][n][0] < INF) ans = min(ans, n);
    if(dp[0][n][1] < 0) ans = min(ans, n);
}