KEYENCE Programming Contest 2019 参加記録＆解説

まあまあの速度で4完。Eは解きたかった…

f:id:betrue12:20190114020636p:plain

本番後に通したEも含めて5問解説します。→Fも書き足しました。

A - Beginning

解法

ソートして 1479 になるかどうかチェックするのが一番楽です。

ACコード

（Ruby）Submission #3998262 - KEYENCE Programming Contest 2019

B - KEYENCE String

解法

文字列 $S$ が100文字以下なので、取り除く範囲を全探索すればよいです。

部分文字列のとり方は各言語によって違いますが、ちゃんと漏れなく列挙できているかどうか不安になりますね…不安な場合は試しに abc などの短い文字列を入力にして、列挙した文字列を全部デバッグ出力して全部あるか確認してみるのが良いと思います。

ACコード

（Ruby）Submission #4000281 - KEYENCE Programming Contest 2019

C - Exam and Wizard

解法

準備度が余っているテストから、準備度が足りないテストに値を移動させます。このとき、そもそも合計値が足りていない場合は条件を満たすことが不可能です。

準備度を変更するテストの個数をなるべく少なくしたいですが、準備度が足りないテストは明らかに変更する必要があるので、準備度の余っているテストの変更数をなるべく少なくしたいです。これは余っている値が大きいものから順番に使っていくと最適になります。

まとめると、準備度が足りないテストの個数と不足値合計を計算しておきます。次に準備度が余っているテストの余剰値を大きい順にソートして、不足値を全部補えるまで大きい方から使っていきます。準備度が足りないテストの個数と、準備度が余っているテストを使った個数の合計が答えです。

ACコード

（C++）Submission #4001678 - KEYENCE Programming Contest 2019

D - Double Landscape

解法

各行と各列の最大値が指定されているので、数を大きいほうから追加していくと上手くいきます。小さい方から追加していくと「最大値のために1つマスを空けておかないといけない」など条件が難しくなりますが、大きい方から追加していくと最大値を追加した後はその行/列に自由に数を追加していけるからです。

ということで大きい方から追加していきますが、例を使ってどのようになるかを見てみます。

f:id:betrue12:20190114030452p:plain

例にあるように、

行最大値と列最大値の両方に登場するときは、その交点に置く。
行最大値だけに登場するときは、既に最大値が置かれている行に置く。逆も同様。
行と列どちらの最大値にも登場しないときは、行にも列にも既に最大値が置かれているようなマスに置く。

という操作をすることになります。この操作を $NM, NM-1, ..., 1$ と最後まで行って、各数字の置ける候補の個数を全部掛け算したものが答えになります。

1.の場合、もちろん候補の数は1つです。

2.の行最大値だけに登場するときは、既に列最大値が登場している列数がそのまま候補の数になります。

3.については、「行にも列にも既に最大値が置かれているような空きマスの個数」が必要です。これは（最大値が置かれた行の数）×（最大値が置かれた列の数）－（既に置いた数字の個数）で求めることができます。

この操作の途中で「置き場所がなくなった」、つまり置く候補の数が0になった場合は、答えは0になります。0に何を掛けても0なのでそのまま処理を続けてもよいですし、すぐに0を出力して終了しても良いです。状態がおかしくなってREになるかもしれないという不安がよぎるので、即終了のほうが安心かもしれません。

ACコード

（C++）Submission #4011139 - KEYENCE Programming Contest 2019

実装においては行最大値と列最大値をそれぞれソートしておくと楽です。これは盤面の行と行、または列と列を入れ替えるという操作に相当し、今回はこの操作によって答えが変わることはないのでソートして大丈夫です。

E - Connecting Cities

解法

コンテスト終了後に公式解説を見て通したので、公式解説ベースの解法で解説します。

作りたいのは最小全域木です。ただし辺の張り方が $O(N^{2})$ 通りあるので、辺の選び方を工夫する必要があります。

辺のコストは都市間の距離 $|i-j|$ と都市の規模 $A_{i}$ に依存していて、「近いから」「規模が小さいから」というだけでは最適な辺を選ぶことはできません。ただし、「近いし規模も小さい」という辺は、「遠いし規模も大きい」という辺よりはコストが小さいはずです。

というわけで、そのような状況を考えてみます。

f:id:betrue12:20190114122008p:plain

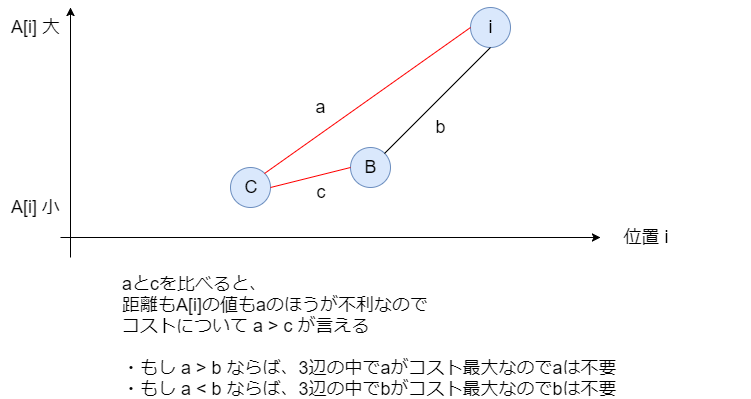
図の縦軸が規模 $A_{i}$ の値で、横軸が位置を表します。このとき辺 $a, c$ を比べると、 $c$ のほうが「近いし規模も小さい」という辺になっています。

ここでさらに図中の $b$ のような辺を考えると、この閉路を作る3辺のうちコストが最大の辺は最小全域木において使うことはありません（クラスカル法のアルゴリズムより）。さきほど見た $a \gt c$ という関係から、 $a, b$ のうちコストが大きいほうが3辺の中でもコスト最大になり、その辺は考える必要がありません。

この考察は規模の等しい都市があったとしても成立します。また辺 $a, b$ のコストがぴったり同じ場合は、どちらを使うと考えてもよいです。

この事実を一般化するために、3点の中で一番 $A_{i}$ が大きい頂点、図中の頂点 $i$ に注目します。そうするとさきほどの事実は

ある頂点 $i$ から見て左右のどちらかを見たときに、そちら側にある「規模が $A_{i}$ 以下である頂点」2つと結ぶ辺のうち、コストが小さいもの1本以外は不要である

と言い換えられ、さらに一般化して

ある頂点 $i$ から見て左右のどちらかを見たときに、そちら側にある「規模が $A_{i}$ 以下である頂点」と結ぶ辺すべてのうち、最もコストが小さいもの1本以外は不要である

と言うことができます。このように考えると、不要でない辺は1つの頂点につき高々2本しかないことが分かります。（これはあくまで規模が小さい都市に「繋ぎに行く」辺の本数であり、規模の自分より規模の大きい都市から「繋がれる」ことである頂点の最終的な次数が2を超えることはあります）

不要でない辺が高々頂点数の2倍であれば、クラスカル法などのアルゴリズムで十分間に合います。

f:id:betrue12:20190114122027p:plain

次は「頂点 $i$ から見て片側にある、規模が $A_{i}$ 以下である頂点のうち、コストが最も小さいものはどれか？」という問題を解く必要があります。区間内最小値ということでセグメント木が使えそうですが、距離の条件があるのでコスト値そのものをセグメント木に入れることはできません。

ただコストの特徴として、例えばある頂点から右側を見る場合、1つ座標が右にずれるごとにコストの距離要素は $+D$ だけ変動します。2つ座標がずれると $+2D$ です。この距離が遠くなることによるコスト差を、最初からセグメント木に含めてしまうという手があります。つまり「右側を見る」用のセグメント木には、

頂点1の要素としては $A_{1} + D$
頂点2の要素としては $A_{2} + 2D$
...
頂点Nの要素としては $A_{N} + ND$

を格納します。こうすれば距離によるコスト差を含んだ上での最小値がどれなのか判断できます。ただこれは「大小関係の比較」をするには正しいですが、頂点 $i$ の位置が考慮されておらず実際のコストそのものではないので、実際のコストは求め直すか頂点 $i$ のぶんを補正しましょう。

「左側を見る」用のセグメント木は別途作って、傾斜を逆にします。またこの問題の場合「最小コストはいくらか」だけでなく「最小コストを実現する頂点はどれか」という情報も必要なので、 (コスト, 頂点番号) の形のペアを格納できるセグメント木を使うとよいです。

規模が自分以下の頂点だけを繋ぎに行く対象にしたいので、「頂点を規模が小さい順にセグメント木に追加しながら、その時点で追加されている頂点の中から繋ぎ先を選ぶ」という処理の流れになります。

このようにすれば不要でない辺の選定も効率的に行うことができるので、最後にクラスカル法で最小全域木のコストを求めればOKです。

ACコード

Submission #4010825 - KEYENCE Programming Contest 2019

F - Paper Cutting

解法

最初の発想

操作列をそのまま列挙するのはもちろん無理です。少し考えると、 $k$ 回目の操作後の破片の個数はその時点での縦の切断数と横の切断数から求めることができて、（破片の数）×（場合の数）みたいなのをどんどん足していけば答え自体は求まります。ただ計算量がかかりすぎてしまいます。

ここで発想を変え、「破片と1対1に対応する何か」を数え上げることができないか考えてみます。今回の場合、「破片の四隅のどこか1つ（例えば、左上隅）」を数えるように考えてみると上手くいきます。

つまり、「 $k$ 回目の切断後に、紙の座標 $(i, j)$ が、破片の左上隅になっている」という条件を満たす場合の数を数えます。これを $i, j, k$ 全てについて合計してあげれば求めたい答えが求まるはずです。

一見変数が多くてやっぱり計算量が多くなりそうですが、この考え方にはとても嬉しい性質があり、それは「座標 $(i, j)$ が破片の左上隅になるような条件は、高々4種類だけに分類できる」ということです。具体例を見てみます。

f:id:betrue12:20190115002812p:plain

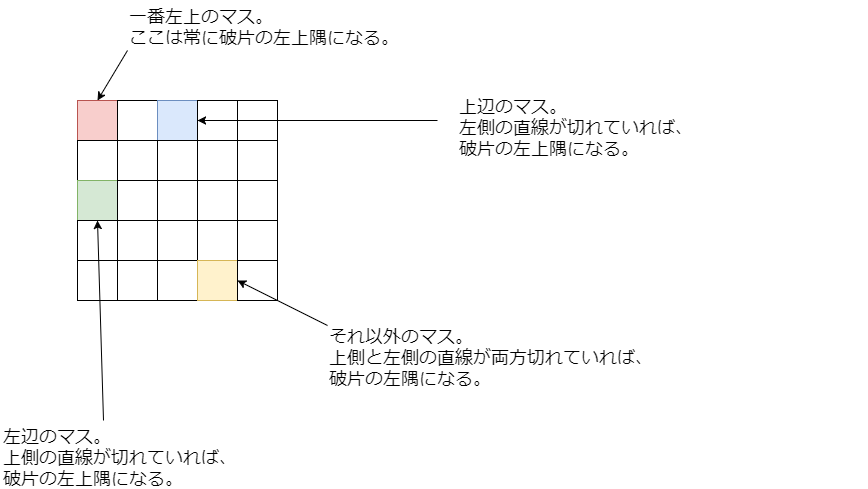
このように、左上隅のマス、上辺のマス（左上隅以外）、左辺のマス（左上隅以外）、それ以外のマスで分類できます。

これらの条件は「常に左上隅になる」「特定の1直線が切れていれば左上隅になる」「特定の2直線が切れていれば左上隅になる」の3種類に分けられて、上辺・左辺の性質もまとめることができます。それぞれのマスの個数も計算することができるので、あとは切断ステップ $k$ ごとに「 $k$ 回目の切断後に、そのマスが左上隅になる条件が満たされている」ような場合の数を求めればよいです。

左上隅

これは簡単です。全部の場合の数を数えればよいです。

$H+W$ 個の直線を順序を付けて $K$ 個並べるので、全部の場合の数は $_{H+W}P_{K}$ になります。切断回数は全部で $K$ 回、マス数は1個なので、これらを全部掛け合わせて

$S_{1} = K \times (_{H+W}P_{k})$

が左上隅についての合計破片数になります。

上辺/左辺

これらのマスが破片の左上隅になる条件は、ある特定の1直線が切断されていることでした。この直線を $a$ と表記します。

$k$ 回目の切断後に直線 $a$ が切断されているような場合の数を考えます。このとき直線 $a$ の入る場所は1回目から $k$ 回目までの $k$ 通りです。そして残りの $K-1$ 回分の切断は何でも良いので、残った直線 $H+W-1$ 本から自由に並べます。このような場合の数の総数は

$k \times _{H+W-1}P_{K-1}$

になります。これは $k$ に依存しているので1回目から $k$ 回目までの和を取って、さらに上辺と左辺のマス数（左上隅以外）のマス数 $H+W$ を掛けて、

$S_{2} = (\sum_{k=1}^{K}k) \times (_{H+W-1}P_{K-1}) \times (H+W) = \frac{1}{2}K(K+1) \times (_{H+W}P_{k})$

となります。 $\sum_{k=1}^{K}k = \frac{1}{2}K(K+1)$ の公式を使っています。

※ちなみに最後の式変形で $(_{H+W}P_{k})$ と全事象数が出ていていますが、確率の考え方を用いると $k$ 回目の切断終了後にある直線 $a$ が切れている確率は $\frac{k}{H+W}$ と求めることができて、（全事象数）×（確率）の計算をすることでも全く同じ式を導くことができます。

それ以外

それ以外の辺が破片の左隅になる条件は、ある特定の2直線が切断されていることでした。この直線を $a, b$ と表記します。

$k$ 回目の切断後に直線 $a, b$ がともに切断されているような場合の数を考えます。このとき、まず直線 $a$ の入る場所は先ほどと同じく $k$ 通り。そして直線 $b$ の入る場所は、 $a$ が入ったぶん空きが1つ少なくなるので $k-1$ 通りです。残りの $K-2$ 回分の切断は何でも良いので、残った直線 $H+W-2$ 本から自由に並べます。このような場合の数の総数は

$k(k-1) \times _{H+W-2}P_{K-2}$

になります。やはり $k$ で和を取ってマス数の合計 $HW$ を掛けると、

$S_{3} = (\sum_{k=1}^{K} k(k-1)) \times (_{H+W-2}P_{K-2}) \times (HW) = \frac{1}{3}K(K-1)(K+1) \times (_{H+W-2}P_{K-2}) \times (HW)$

となります。前2つと違ってあまりキレイな式にはなりません。 $\sum$ の計算は先ほどの公式と $\sum_{k=1}^{K}k^{2} = \frac{1}{6}K(K+1)(2K+1)$ の公式で展開して変形するとこうなりますが、 $k(k-1)$ の和を $O(K)$ で素直に求めても良いと思います。