ARMERIA

Rubyと競技プログラミングの話　AtCoderやCodeforcesの問題解説記事が多め。

Educational Codeforces Round 65 E. Range Deleting

Codeforces プログラミング競技プログラミング

Problem - E - Codeforces

問題概要

長さ $n$ の数列 $\lbrace a_{i} \rbrace$ と整数 $x$ が与えられ、 $1 \le a_{i} \le x$ である。

以下の条件を満たす整数の組 $(l, r)$ の個数を求めよ。

$1 \le l \le r \le x$ である。
数列 $\lbrace a_{i} \rbrace$ から $l \le a_{i} \le r$ を満たす要素をすべて取り除くと、残った数列は広義単調増加になる。（空数列でも可）

制約

$1 \le n, x \le 10^{6}$
$1 \le a_{i} \le x$

解説

削除する値の範囲 $\lbrack l, r \rbrack$ について、ある左端 $l$ を固定したとき、条件を満たす $r$ には単調性があります。これは区間を伸ばせば伸ばすほど多くの要素が消え、残った数列が単調増加になりやすいからです。

二分探索かしゃくとり法が使えないか考えてみましょう。二分探索ができれば楽ですが、 $x$ 個の左端を全探索した上で判定問題を解くのに $n$ 要素の数列を走査しているようでは間に合いません。しゃくとり法を用いて、かつ区間に値を出し入れする処理を何らかの方法で差分更新できれば間に合いそうです。

この差分更新は様々な方法で実現している人がいました。この記事では私が本番中に実装したやり方をまとめておきます。

ある要素 $a_{i}$ に注目します。数列を左から右に並べたときに、もしこの要素より左にあって $a_{i}$ より大きい要素があると数列は単調増加になりません。そのため条件を満たすためには、インデックス $i$ に関して

$a_{i}$ が削除される。
$i$ より左にあって $a_{i}$ より大きい要素の最小値を $m_{i}$ 、最大値を $M_{i}$ として、範囲 $\lbrack m_{i}, M_{i} \rbrack$ が全て削除される。

の少なくとも一方が満たされる必要があります。ただし $i$ より左に $a_{i}$ より大きい要素が存在しないような $i$ については常に条件が満たされていると考えてよいです。

f:id:betrue12:20190516222708p:plain

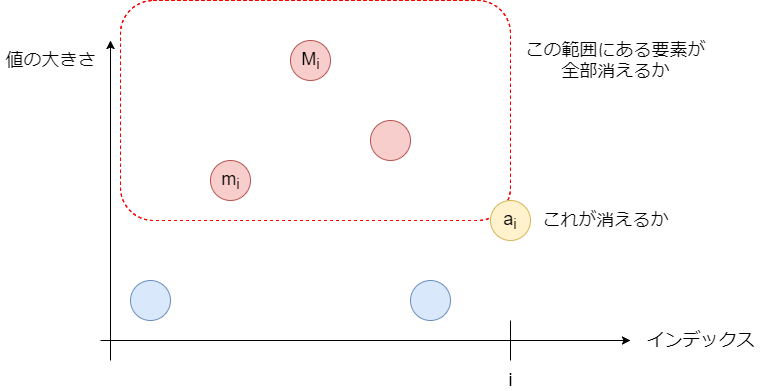
逆に全ての $i$ についてこれらの条件の少なくとも一方が満たされるとき、数列は単調増加になります。

そこでまず、それぞれの $i$ について $m_{i}, M_{i}$ を求めます。これは数列を左から見ていきながらsetやセグメント木に値を追加していくことで合計 $O(N \log N)$ で実現できます。

そしてしゃくとり法を以下のように処理していきます。

区間の右端に値を加えるときには、
- $a_{i} = v$ である $i$ について、条件1を「満たす」に変更する。
- $M_{i} = v$ である $i$ について、もし $l \le m_{i}$ ならば条件2を「満たす」に変更する。
区間の左端から値を取り除くときには、
- $a_{i} = v$ である $i$ について、条件1を「満たさない」に変更する。
- $m_{i} = v$ である $i$ について、もし $M_{i} \le r$ ならば条件2を「満たさない」に変更する。
上記の変更に伴って、「今、条件がどちらも満たされていないインデックス $i$ の個数」を差分更新する。

このようにすれば、区間に値を出し入れして差分更新する処理は合計で $O(N+X)$ になります。合計で $O(N\log N+X)$ となり、制約が大きいのでギリギリですが一応間に合いました。

ACコード

Submission #54241812 - Codeforces