ABC116 解説
AtCoder Beginner Contest 116 - AtCoder
こどふぉと被っていたので参加しませんでした…
A - Right Triangle
解法
三角形の面積は(底辺長)×(高さ)÷2ですね。直角三角形の場合、底辺長と高さは直角を挟む2辺の長さと考えることができます。これを計算しましょう。
ACコード
を見落とすと無駄にソートすることになります。
B - Collatz Problem
解法
この問題の操作は数学においては有名で、どの正の数から始めてもこの操作を続けると有限回で のループに到達する…ということが予想されています。「コラッツの予想」と呼ばれる未解決問題です。
さて問題文の表現が少し回りくどいですが、「前に出た数と同じものが初めて出現したときのインデックス」を求めればよいです。ということでこれまでに出た数をsetなどで持っておけば「同じものが出た」判定をすることができます。
ACコード
C - Grand Garden
解法
一番左の花から考えていきます。この花の高さが足りない場合、この花を左端とするある範囲に水をあげなければいけません。
ではこの範囲はどのように取るべきでしょうか?できるだけ多くの花に水をあげたほうが効率が良さそうな気がします。実際にこれは「伸ばせるだけ伸ばす」、つまり既に花の高さが足りている花の直前まで範囲を長く取るのが最適となります。これについては以前似たような問題の解説を書いているので、そちらも参考にしてください。
ということで、左から1つずつ見ていって、既に高さが足りている花に当たるまで花の高さを1ずつ足していきます。これを一番左の花の高さが足りるまで繰り返します。
一番左の花の高さが足りたら、次は左から2番目の花を左端として同じように考えます。これを最後の花まで繰り返すと答えが求められます。
計算量的には かかる素朴なやり方ですが、制約が小さいのでこれで間に合います。もっと速く解くやり方もありますね。
ACコード
実装は問題の操作とは逆に、「 を受け取り、全部0になるまで値を引いていく」と書くと楽です。もちろん、問題の通り「今の花の高さ」を別途配列で用意して値を足していく実装でも解けます。
D - Various Sushi
解法
この問題は解説が難しいですね…
まず、最適な寿司の選び方というものがどのような性質を持っているか考えてみます。例えば入力として
7 3 1 9 1 8 1 7 2 6 2 1 3 2 3 1
というものを考えてみましょう。このテストケースに対する最適な選び方は以下の図の赤色のものになります。

満足ポイント が最適値です。単体の美味しさ優先で
を取ると25ポイント、種類数優先で
を取ると26ポイントで最適になりません。単体の美味しさと種類数、どちらかを無視した貪欲はうまくいかないことが分かります。
このような最適な寿司の選び方が満たす性質があります。それは、「選んだ 個の寿司は、選ばなかった種類のどの寿司よりも、美味しさが大きいか等しい」という点です。
その理由は、もし選ばなかった種類の寿司の中に選んだ寿司より大きい美味しさを持つものがあれば、寿司を交換することで種類数・美味しさポイントともに有利になり、絶対に満足ポイントが高くなるからです。最適な選び方というからには、より満足ポイントが高い選び方は他に存在しないはずです。
この性質から、もし最適な選び方における寿司の種類数が分かっているならば、次のような方法で最適な選び方を求めることができます。種類数を とします。
- まず全ての種類の寿司から、それぞれの種類で一番美味しい寿司を1つずつ取り出しておき、それらの寿司から美味しい順に
個選ぶ。
- 上記で選ばれなかった2番手以降の寿司を集めて、それらの寿司から美味しい順に
個選ぶ。
さきほどの性質を満たすと何故このような選び方で最適になるのかは、以下のように説明できます。
- 選んだ寿司は選ばなかった種類のどの寿司より大きいという性質、そして
種類の寿司を選ぶということから、まず各種類のベスト寿司を集めて大きい方から
個取ることができます。
- 残りの寿司に関しては、「さっき選んだ
個と同じ種類から美味しい順に
個選ぶ」という選び方をします。これもまた先ほどの性質のおかげで、単に2番手以降の寿司を集めて上から取れば自然とこのような選び方になります。
こうすることで、「各種類のベスト寿司」と「2番手以降の寿司」を独立に選ぶことができる点が嬉しいです。
肝心の最適な種類数 はまだ分かっていませんが、
を全探索すればどこかで最適値が見つかるはずです。このとき上記のやり方で寿司を選んだときの満足ポイントは
(各種類のベスト寿司の、上から 個の美味しさ和)+(2番手以降の寿司の、上から
個の美味しさ和)+
で求められます。それぞれの「上から○○個の美味しさ和」は事前にソートして累積和を取っておくことで高速に求められるため、 を全探索しても十分に間に合います。
ACコード
- (Ruby)Submission #4059488 - AtCoder Beginner Contest 116
- (C++)Submission #4079852 - AtCoder Beginner Contest 116
この解説では、解法の正しさが比較的納得しやすいような説明を採用しました。「最適な選び方が持っている性質を考える」ということは1つの重要な視点ですね。ただ、コンテスト本番では「種類数の項が厄介だから、まずそこを固定して全通り試そう」という発想からスタートするほうが自然かな、とは思います。
DDCC2019 参加記
行ってきましたDDCC!
コード部門の解説記事は別途書いたので、こちらの記事ではイベントそのものの参加記を雑多に書いていこうかと思います。
会場で全然写真を撮っていないのでDDCC公式さんのツイートをペタペタ貼らせていただきます。
開始前
集まってきましたね〜 #ddcc2019 pic.twitter.com/bFJCRDx0Nt
— ddcc2019 (@ddcc_2019) January 19, 2019
会場はこんなところでした。普段はカフェテリアになっているそうです。200人集まるだけあってかなり広い。
暑すぎてディスコTに着替えた
— アルメリア (@armeria_betrue) January 19, 2019
会場内の気温が半袖Tシャツに最適化されている
DDCC Tシャツをいただきました。着替えどうしようかなと思いましたが…会場が半袖基準なのか!?と思うくらい暑かったので着替え。
前に円盤状のウェーハが飾られているのを見て「これが例のアレ…」と思いましたが、実はそれが上位3名に贈られるDISCO特製賞状(状?)でした。
貼った pic.twitter.com/UO4jyn7xP4
— アルメリア (@armeria_betrue) July 28, 2018
PCにこのステッカーを貼っていたら横を通ったchokudaiさんに発見されました。
コード部門
AB2完(40:25)で205人中95位でした。
本番の流れとしては、
- Aは普通に通す(6:30)
- Bはパッと見てよく分からなかったのでEの600点を狙いに行く(~30:00くらいまでここで使ってしまった)
- Bに戻って解法に気づきAC(40:25)
- C, Dをチラ見しつつEを考える…も分からず(~100:00くらいまで)
- Dの方針が浮かぶも、実装が間に合わず終了(~120:00)
みたいな感じでした…
素直に解いている人が多いDに早く移るべきだったのかなあとは思います。TL13秒にビビリました。
DDCC2019 D - DISCO! https://t.co/ip6dXgXGuL
— アルメリア (@armeria_betrue) January 19, 2019
通した。本番考えてたので方針は合ってたみたい…
↑本番後に通しました
昼食
もうすぐでビュッフェ❤️#ddcc2019 pic.twitter.com/H05FUhL1j4
— ddcc2019 (@ddcc_2019) January 19, 2019
ここでTwitterなどで知っている人を探す…も、ほとんどの人は名札のAtCoder IDでしか判別できないのですれ違う人々の名札を見る怪しい人に。声を掛けていただけることも多かったのでとてもありがたかったです。1stエンカウントはJoeさん&けんしんさんでした。
既にお会いしたことのあるてんぷらさん、その繋がりでつたじぇーさん&ほげもちさんなどなどたくさんの方々と会うことができました。ありがとうございました!
話題を振るのが下手なのでひたすら競プロの話をしていたのですが、「この前のコンテストのあの問題が…」みたいな話を振っても普通に通じるの、改めて考えると凄いことですね。
ご飯はあんまり食べてないです。ひたすら喋ってました…
装置実装部門(予選)
動いてた。#ddcc2019 pic.twitter.com/1PLRR5vHOS
— ddcc2019 (@ddcc_2019) January 19, 2019
お昼休みの時点で用意されていたこの機械。装置実装部門はこの機械を使ってのコンテストで、予選はAtCoder上のシミュレータで行われました。(URLはありますが、非ログイン状態だとNot Found表示になるので、参加者しか問題を見れないものと思われます)
いわゆるマラソン形式なのですがこれが大変厳しく、長い問題文の中に制約が散らばっていてこれらを守れないと即WA、事前情報無しで制限時間は30分…と、その結果正の得点を取れたのが205人中19人。
— アルメリア (@armeria_betrue) January 19, 2019
コンテストが終わった瞬間に会場には笑いが…これはこれで貴重な経験でした。初回の試みなので、次回以降より良くなるよう期待したいところですね。
DISCO社内ツアー
せっかくなので参加希望を出していました。学生でもないのにスミマセン。
ダーツ、ビリヤード台、トレーニングジム、プールなどなど色々ありました。お蕎麦屋さんを吸収合併(?)した話が面白かったです。
あと会社のビルがそのまま寮にもなっているようで…気分的に会社に住みたいかはともかく、通勤時間ほぼゼロは良いですね。
実際に円盤状のウェーハを加工するところも見ることができました。
終わった後は時間があったので適当に喋ってました。かなり自由に交流できる時間があったように思います。
装置実装部門(決勝)
装置動かしてますよー!#ddcc2019 pic.twitter.com/pks2LubuOi
— ddcc2019 (@ddcc_2019) January 19, 2019
決勝はこんな感じで装置の周りに集まり、予選上位10人がプログラムを動かしました。
写真だとわかりにくいですが、緑と赤のランプがあるところから水が出ます。ビーカー(写真だと右手前にある黄色っぽいもの)をプログラムで制御して、2箇所で水を受ける→スミの排出穴に落とすという動作をいかに速く、かつこぼさずにできるか…という競技です。
10人皆さんのプログラムの動きにかなり特徴があって、観ているだけでかなり盛り上がりました。1位のyosupoさんの動きは、無駄なく速くこぼさずに…という、流石1位という感動的な動き方でした。競プロすごい(?)
これは素晴らしいイベントだと思いました。次回も改善・強化して是非やってほしいです。
表彰式
表彰式🏆#ddcc2019 pic.twitter.com/vpB1vNXnVX
— ddcc2019 (@ddcc_2019) January 19, 2019
装置実装部門1位はさっきの決勝時点で既に分かっていましたが、なんとコード部門でもyosupoさんが優勝。まさか2部門独占優勝になるとは…本当にすごい。
懇親会
ここでもご飯を食べながら色々な人とお話。
競技プログラミングを始めたのは相対的に見ると最近のほうではありますが、結構たくさんの方に知ってもらえていて。あと「ブログの解説見てます」と言っていただけてとてもありがたいです。
あと、名札に書いていたAtCoder IDに普段名乗っているアルメリアという名前が入っていないので、次からは見つけてもらいやすいように自前の名札を持っていこうと思いました…
みなさんご参加いただき、ありがとうございました🙌
— ddcc2019 (@ddcc_2019) January 19, 2019
集合写真🔽 #ddcc2019 pic.twitter.com/gAvCzyQSqS
最後に写真撮影をして終わり。皆さんありがとうございました!
おまけ
体重実装部門です #DDCC2019 pic.twitter.com/pgYOj1CSBN
— アルメリア (@armeria_betrue) January 19, 2019
昼も夜も会場であまり食べていなかったので帰り道でご飯。「さぼてん」というお店です。オススメ。
最後に
オンサイトコンテストの参加は昨年7月のSoundHoundコンテスト以来で、そのときは社会人限定というちょっと特殊な感じでしたが、今回は幅広く205人もの人が参加していて色々な人と会うことができました。
もちろんメインはコンテストで競い合うというイベントですし、主催企業さんにとっては特に学生さん向けに自社をアピールする機会ではありますが…普段オンラインで繋がっている競プロerと実際に会って交流できるというのはやっぱり一番大きな魅力だと思います。この場を用意してくれた方々に本当に感謝です。「コンテスト楽しかったなあ」というのは会社名とともに記憶に強く残りますよね。
私自身はもう社会人なので、今回のように社会人にも多い枠が用意されているコンテストにしか参加できないとは思いますが…これからもできる限りオンサイトコンテストに参加したいですし、特に次回のDDCCにも是非行きたいですね。精進あるのみです。

DDCC2019 参加記録(コード部門)&解説(A, B, D)
今回はオンサイト参加でした!
コード部門以外のもろもろ参加記はまた別途書こうかなと思っています。この記事ではいつものように問題の解説を。

本番はAB2完でしたが…A, B, D問題について書きます。
A - レース (Race)
解法
連続した氷マスの長さに応じて所要時間が変わるので、連続した氷マスそれぞれの塊について考えます。
雪マス1つを氷マスに変えたとき、もし別々の氷マスの塊が結合してしまうようであれば厄介ですが、制約からそのようなことは起こりません。そのため、氷マスを1つ増やして一番得になる氷マスの塊に付けることを考えればよく、それは最も長い氷マスの塊になります。
あとは実際に計算です。私のコードではまず氷マスの塊の長さを全て列挙し、一番大きい要素に1加え(氷マスが1つもない場合に注意)、最後に計算しています。
ACコード
- (Ruby)Submission #4039170 - DISCO presents ディスカバリーチャンネル コードコンテスト2019 本戦
- (C++)Submission #4049505 - DISCO presents ディスカバリーチャンネル コードコンテスト2019 本戦
B - 大吉数列 (Array of Fortune)
解法
かつ
を満たすペア
の個数というものは、「転倒数」によく似ています。実際、
とするとこれは順列の転倒数そのものになります。この記事ではこのペアの個数を
転倒数と呼ぶことにします。
転倒数が最大になるのは数列が逆順ソートされているときでした。 転倒数が最大になるのも、同様に数列が逆順ソートされているときです。まずはその個数を求めます。

図に示すように、長さ の順列を逆順ソートしたときの
転倒数は、
を全て足したものになり、計算すると
です。与えられた
がこの値より大きい時は、どうやっても条件を満たせないので
No Luck で終了です。以降、そうでないときに数列を構成する方法を考えます。
まず という正順ソートされた数列を考えると、この数列の
転倒数はもちろん0です。この数列の末尾要素
を先頭に移動させると、
までの要素との位置関係が逆になります。このうち
の値に対して
転倒数が増えるため、
転倒数は
増えます。
次に を2番目に移動させると、同じように
転倒数は
増えます。このように「末尾の要素
を数列の
番目に移動させてきて、
転倒数を
個増やす」という操作を、
転倒数が
を超えないところまで繰り返します。(「
番目」は0-indexedです)
最後は 転倒数をぴったり
に合わせるために微調整をする必要があります。といっても、同じように末尾の要素
を数列の
番目に移動させた後、増えすぎたぶんを戻すために1つずつ後ろに戻していくと考えると楽です。後ろに戻すときは
といった小さい値から順に位置関係が戻っていくため、ぴったり
になるまでは1つ戻すごとに
転倒数が1減っていきます。

あとはこれを実装します。私の実装では全要素 (空いていることを示す)で初期化したvectorを用意し、
転倒数が
になるまでは大きいほうから値を埋めていって、最後に空いているところに小さいほうから値を入れています。
ACコード
D - DISCO!
公式解説とは違う方法で解いたので、その方法を書きます。
解法
もしクエリの全てが 、つまり常に先頭からある右端までの部分列
DISCO の個数を答えるのであれば簡単です。「 の先頭から
文字目までに含まれる、
DISCO のうち 文字目までの部分列の個数」を
とするDPをしておけばよいです。この場合の答えは
です。
今回の問題の場合は も様々な値を取りますが、
のときの応用で解けないか考えてみます。
与えられたクエリ に対して、まず区間
に含まれる部分列
DISCO の個数が先ほどのDPで分かっているとします。この個数をいくつかのパターンに分解します。

求めたいのはこのパターンのうち一番上のものなので、それ以外の値を全て引けば答えが求められるはずです。
これらの値の求め方を考えます。例えばD | ISCO と分断されているパターンについて、この個数は区間 に含まれる
D の個数と区間 に含まれる
ISCO の個数の積です。前者は です。次に後者ですが…これは元のクエリで問われている値の、頭の文字数が1文字少ないバージョンになっています。必要なDPテーブルの値さえ分かっていれば、これは今まで書いてきた方法と全く同じように求められるはずです。
DI | SCO と分断した場合も、区間 に含まれる
DI の個数と区間 に含まれる
SCO の個数として同様に求められます。 DIS | CO、DISC | O についても同様です。最後の DISCO | となっているパターンは、 そのものです。
ここまでの議論を一般化します。「区間 の間に含まれる、
DISCO の末尾 文字と一致するような部分列の個数」を
と置くと、クエリの答えは
です。そしてこの値は先ほどの図で示したやり方を用いて、
の値と、前計算したDPテーブルの値を用いて計算することができます。
このときDPテーブルの値は少し拡張する必要があって、例えば の計算では
ISCO の個数を求めなければいけないので、先頭からの ISCO や I IS などの個数が必要となります。そのため、「 の先頭から
文字目までに含まれる、
DISCO のうち 文字目から
文字目までの部分列の個数」を
とするDPテーブルを全て計算しておけば必要な値が揃います。
あとは の計算をきちんと立式できれば解けます。クエリごとにメモ化することで計算時間を短縮できますが、制限時間がとても長いのでしなくても間に合うんじゃないかと思います。
計算量については、DISCO の長さは大きく影響するので として表記に入れ込むことにします。メモ化した場合、DPとクエリ処理合わせて
となります。
ACコード
制限時間13秒のおかげでRubyでも通ります。
KEYENCE Programming Contest 2019 参加記録&解説
まあまあの速度で4完。Eは解きたかった…

本番後に通したEも含めて5問解説します。→Fも書き足しました。
A - Beginning
解法
ソートして 1479 になるかどうかチェックするのが一番楽です。
ACコード
B - KEYENCE String
解法
文字列 が100文字以下なので、取り除く範囲を全探索すればよいです。
部分文字列のとり方は各言語によって違いますが、ちゃんと漏れなく列挙できているかどうか不安になりますね…不安な場合は試しに abc などの短い文字列を入力にして、列挙した文字列を全部デバッグ出力して全部あるか確認してみるのが良いと思います。
ACコード
C - Exam and Wizard
解法
準備度が余っているテストから、準備度が足りないテストに値を移動させます。このとき、そもそも合計値が足りていない場合は条件を満たすことが不可能です。
準備度を変更するテストの個数をなるべく少なくしたいですが、準備度が足りないテストは明らかに変更する必要があるので、準備度の余っているテストの変更数をなるべく少なくしたいです。これは余っている値が大きいものから順番に使っていくと最適になります。
まとめると、準備度が足りないテストの個数と不足値合計を計算しておきます。次に準備度が余っているテストの余剰値を大きい順にソートして、不足値を全部補えるまで大きい方から使っていきます。準備度が足りないテストの個数と、準備度が余っているテストを使った個数の合計が答えです。
ACコード
D - Double Landscape
解法
各行と各列の最大値が指定されているので、数を大きいほうから追加していくと上手くいきます。小さい方から追加していくと「最大値のために1つマスを空けておかないといけない」など条件が難しくなりますが、大きい方から追加していくと最大値を追加した後はその行/列に自由に数を追加していけるからです。
ということで大きい方から追加していきますが、例を使ってどのようになるかを見てみます。

例にあるように、
- 行最大値と列最大値の両方に登場するときは、その交点に置く。
- 行最大値だけに登場するときは、既に最大値が置かれている行に置く。逆も同様。
- 行と列どちらの最大値にも登場しないときは、行にも列にも既に最大値が置かれているようなマスに置く。
という操作をすることになります。この操作を と最後まで行って、各数字の置ける候補の個数を全部掛け算したものが答えになります。
1.の場合、もちろん候補の数は1つです。
2.の行最大値だけに登場するときは、既に列最大値が登場している列数がそのまま候補の数になります。
3.については、「行にも列にも既に最大値が置かれているような空きマスの個数」が必要です。これは (最大値が置かれた行の数)×(最大値が置かれた列の数)-(既に置いた数字の個数)で求めることができます。
この操作の途中で「置き場所がなくなった」、つまり置く候補の数が0になった場合は、答えは0になります。0に何を掛けても0なのでそのまま処理を続けてもよいですし、すぐに0を出力して終了しても良いです。状態がおかしくなってREになるかもしれないという不安がよぎるので、即終了のほうが安心かもしれません。
ACコード
(C++)Submission #4011139 - KEYENCE Programming Contest 2019
実装においては行最大値と列最大値をそれぞれソートしておくと楽です。これは盤面の行と行、または列と列を入れ替えるという操作に相当し、今回はこの操作によって答えが変わることはないのでソートして大丈夫です。
E - Connecting Cities
解法
コンテスト終了後に公式解説を見て通したので、公式解説ベースの解法で解説します。
作りたいのは最小全域木です。ただし辺の張り方が 通りあるので、辺の選び方を工夫する必要があります。
辺のコストは都市間の距離 と都市の規模
に依存していて、「近いから」「規模が小さいから」というだけでは最適な辺を選ぶことはできません。ただし、「近いし規模も小さい」という辺は、「遠いし規模も大きい」という辺よりはコストが小さいはずです。
というわけで、そのような状況を考えてみます。
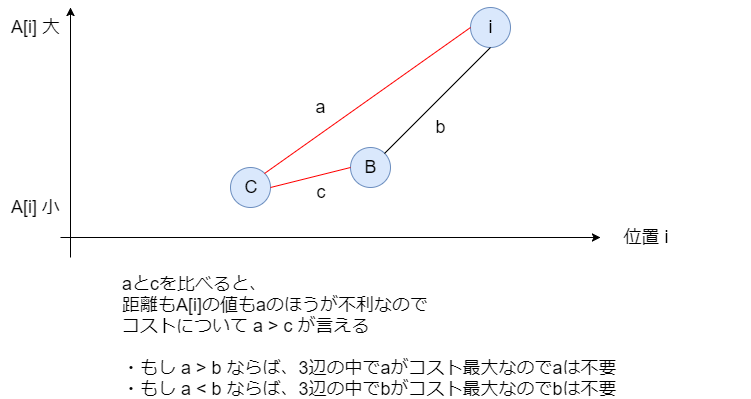
図の縦軸が規模 の値で、横軸が位置を表します。このとき辺
を比べると、
のほうが「近いし規模も小さい」という辺になっています。
ここでさらに図中の のような辺を考えると、この閉路を作る3辺のうちコストが最大の辺は最小全域木において使うことはありません(クラスカル法のアルゴリズムより)。さきほど見た
という関係から、
のうちコストが大きいほうが3辺の中でもコスト最大になり、その辺は考える必要がありません。
この考察は規模の等しい都市があったとしても成立します。また辺 のコストがぴったり同じ場合は、どちらを使うと考えてもよいです。
この事実を一般化するために、3点の中で一番 が大きい頂点、図中の頂点
に注目します。そうするとさきほどの事実は
- ある頂点
から見て左右のどちらかを見たときに、そちら側にある「規模が
以下である頂点」2つと結ぶ辺のうち、コストが小さいもの1本以外は不要である
と言い換えられ、さらに一般化して
- ある頂点
から見て左右のどちらかを見たときに、そちら側にある「規模が
以下である頂点」と結ぶ辺すべてのうち、最もコストが小さいもの1本以外は不要である
と言うことができます。このように考えると、不要でない辺は1つの頂点につき高々2本しかないことが分かります。(これはあくまで規模が小さい都市に「繋ぎに行く」辺の本数であり、規模の自分より規模の大きい都市から「繋がれる」ことである頂点の最終的な次数が2を超えることはあります)
不要でない辺が高々頂点数の2倍であれば、クラスカル法などのアルゴリズムで十分間に合います。

次は「頂点 から見て片側にある、規模が
以下である頂点のうち、コストが最も小さいものはどれか?」という問題を解く必要があります。区間内最小値ということでセグメント木が使えそうですが、距離の条件があるのでコスト値そのものをセグメント木に入れることはできません。
ただコストの特徴として、例えばある頂点から右側を見る場合、1つ座標が右にずれるごとにコストの距離要素は だけ変動します。2つ座標がずれると
です。この距離が遠くなることによるコスト差を、最初からセグメント木に含めてしまうという手があります。つまり「右側を見る」用のセグメント木には、
- 頂点1の要素としては
- 頂点2の要素としては
- ...
- 頂点Nの要素としては
を格納します。こうすれば距離によるコスト差を含んだ上での最小値がどれなのか判断できます。ただこれは「大小関係の比較」をするには正しいですが、頂点 の位置が考慮されておらず実際のコストそのものではないので、実際のコストは求め直すか頂点
のぶんを補正しましょう。
「左側を見る」用のセグメント木は別途作って、傾斜を逆にします。またこの問題の場合「最小コストはいくらか」だけでなく「最小コストを実現する頂点はどれか」という情報も必要なので、 (コスト, 頂点番号) の形のペアを格納できるセグメント木を使うとよいです。
規模が自分以下の頂点だけを繋ぎに行く対象にしたいので、「頂点を規模が小さい順にセグメント木に追加しながら、その時点で追加されている頂点の中から繋ぎ先を選ぶ」という処理の流れになります。
このようにすれば不要でない辺の選定も効率的に行うことができるので、最後にクラスカル法で最小全域木のコストを求めればOKです。
ACコード
Submission #4010825 - KEYENCE Programming Contest 2019
F - Paper Cutting
解法
最初の発想
操作列をそのまま列挙するのはもちろん無理です。少し考えると、 回目の操作後の破片の個数はその時点での縦の切断数と横の切断数から求めることができて、(破片の数)×(場合の数)みたいなのをどんどん足していけば答え自体は求まります。ただ計算量がかかりすぎてしまいます。
ここで発想を変え、「破片と1対1に対応する何か」を数え上げることができないか考えてみます。今回の場合、「破片の四隅のどこか1つ(例えば、左上隅)」を数えるように考えてみると上手くいきます。
つまり、「 回目の切断後に、紙の座標
が、破片の左上隅になっている」という条件を満たす場合の数を数えます。これを
全てについて合計してあげれば求めたい答えが求まるはずです。
一見変数が多くてやっぱり計算量が多くなりそうですが、この考え方にはとても嬉しい性質があり、それは「座標 が破片の左上隅になるような条件は、高々4種類だけに分類できる」ということです。具体例を見てみます。
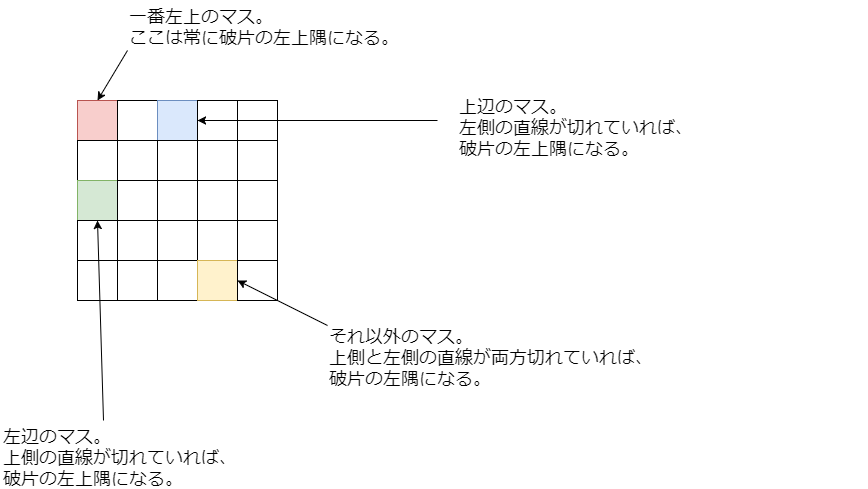
このように、左上隅のマス、上辺のマス(左上隅以外)、左辺のマス(左上隅以外)、それ以外のマスで分類できます。
これらの条件は「常に左上隅になる」「特定の1直線が切れていれば左上隅になる」「特定の2直線が切れていれば左上隅になる」の3種類に分けられて、上辺・左辺の性質もまとめることができます。それぞれのマスの個数も計算することができるので、あとは切断ステップ ごとに「
回目の切断後に、そのマスが左上隅になる条件が満たされている」ような場合の数を求めればよいです。
左上隅
これは簡単です。全部の場合の数を数えればよいです。
個の直線を順序を付けて
個並べるので、全部の場合の数は
になります。切断回数は全部で
回、マス数は1個なので、これらを全部掛け合わせて
が左上隅についての合計破片数になります。
上辺/左辺
これらのマスが破片の左上隅になる条件は、ある特定の1直線が切断されていることでした。この直線を と表記します。
回目の切断後に直線
が切断されているような場合の数を考えます。このとき直線
の入る場所は1回目から
回目までの
通りです。そして残りの
回分の切断は何でも良いので、残った直線
本から自由に並べます。このような場合の数の総数は
になります。これは に依存しているので1回目から
回目までの和を取って、さらに上辺と左辺のマス数(左上隅以外)のマス数
を掛けて、
となります。 の公式を使っています。
※ちなみに最後の式変形で と全事象数が出ていていますが、確率の考え方を用いると
回目の切断終了後にある直線
が切れている確率は
と求めることができて、(全事象数)×(確率)の計算をすることでも全く同じ式を導くことができます。
それ以外
それ以外の辺が破片の左隅になる条件は、ある特定の2直線が切断されていることでした。この直線を と表記します。
回目の切断後に直線
がともに切断されているような場合の数を考えます。このとき、まず直線
の入る場所は先ほどと同じく
通り。そして直線
の入る場所は、
が入ったぶん空きが1つ少なくなるので
通りです。残りの
回分の切断は何でも良いので、残った直線
本から自由に並べます。このような場合の数の総数は
になります。やはり で和を取ってマス数の合計
を掛けると、
となります。前2つと違ってあまりキレイな式にはなりません。 の計算は先ほどの公式と
の公式で展開して変形するとこうなりますが、
の和を
で素直に求めても良いと思います。
最後に答えを計算
これらを全て計算すれば のmodを取ったものが答えになります。
必要な道具は高々 までの階乗なので計算量は
で、
といつもより大きめの制約ですが十分間に合います。
ACコード
Submission #4014003 - KEYENCE Programming Contest 2019
コードは数学をして求めた計算式をただ並べているだけという感じですが… が64bitでもオーバーフローするのでそこだけ注意です。
AISing Programming Contest 2019 参加記録&解説
AISing Programming Contest 2019 - AtCoder
全完!
2000未満ratedコンテストだったのでパフォーマンスは付かず、ちょっと残念。

A - Bulletin Board
解法
縦の位置が 通り、横の位置が
通りあるので、これらを掛け算したものが答えです。
ACコード
B - Contests
解法
「1問目になるもの」「2問目になるもの」「3問目になるもの」がそれぞれ排他、つまり点数の範囲が被っていないことが重要です。それぞれの問題数を数えて、一番小さいものを出力すればよいです。
ACコード
C - Alternating Path
解法
黒→白→黒→白…と移動することは、「今いるマスと違う色のマスに移動する」ことと考えることができます。そう考えると、違う色で隣り合っているマスは「相互に行き来できるマス」ということになります。
この相互に行き来できるマス同士を繋いでいくと、グリッドの中で「この範囲内はどのマスからどのマスへも相互に行き来できる」という領域ができます。そうするとこの領域内の黒のマス数×白のマス数だけ、問題の条件を満たすペアを作ることができます。これを領域ごとに数えて全部足すと答えになります。
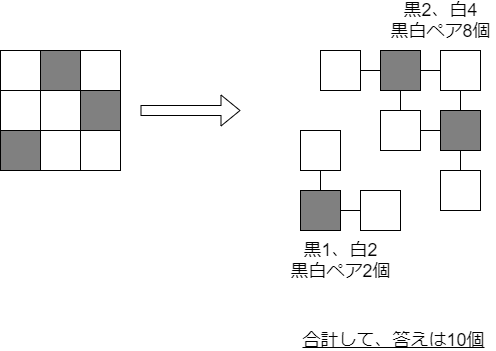
あとは「領域の調べ方、数え方」ですが、これは幅優先探索/深さ優先探索などが楽だと思います。あるマスから始めて、違う色で隣り合っている未訪問のマスを探索していけばよいです。
ACコード
- (Ruby)Submission #3996066 - AISing Programming Contest 2019
- (C++)Submission #3996081 - AISing Programming Contest 2019
D - Nearest Card Game
解法
ここから難易度が上がるので、解説もしっかりしていきたいと思います…
二人が取るカードの全体像を掴む
たくさんの の値について答えを出さなくてはいけませんが、まずは一旦それを忘れて、ある1つの
について考えます。
問題の操作から、高橋くんと青木くんがどのようにカードを取っていくか考えてみます。
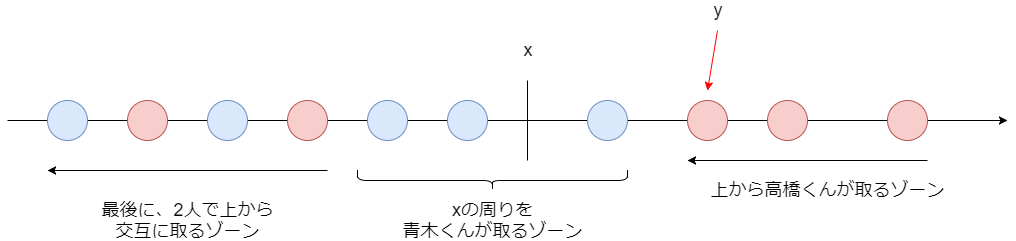
全体の形としてはこのようになります。まず高橋くんは大きいほうから、青木くんは の周りからカードを取っていきます。こうするといずれ高橋くんが青木くんの取っていた領域に当たってしまうので(図中の
のあたり)、その後は2人で交互に残った下の方のカードを大きい方から取っていきます。
もちろん、このうちどこかの領域は要素数がゼロかもしれません。例えば がものすごく大きいところにある場合、2人は単に一番上から交互にカードを取っていくだけになります。
「境界」を探す
これらのゾーンの境界が知りたくなります。境界が分かってしまえば、累積和を用いて高橋くんのカードの合計が分かりそうです。
より上にあるカードについて、そのカードを高橋くんと青木くんどちらが取るのか?を考えます。これを知るには、高橋くんと青木くんそれぞれについて「その人がそのカードを取るとしたら、何枚目に取るか?」を考えればよいです。
取る順番が早いほうがそのカードを取ります。同順の場合は先攻の高橋くんが取ります。
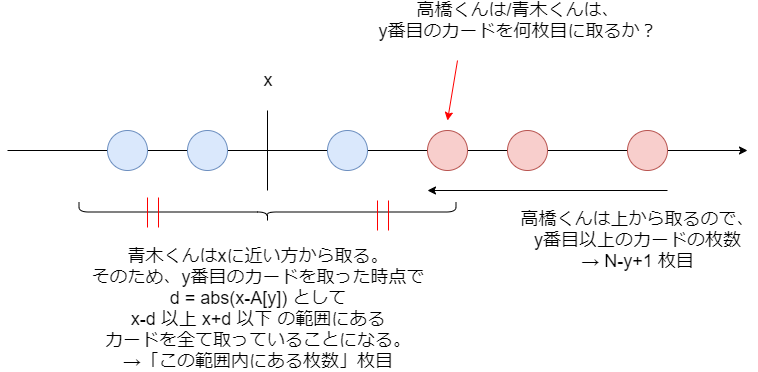
高橋くんのほうは簡単で、一番上から取っていくので「そのカード以上にあるカードの枚数」がそのまま使えます。
青木くんのほうは少しだけ厄介ですが、 に近いところから取る、距離が同じ場合は小さい方を先に取る、という条件から、カード
を取る時点で青木くんは、
として
以上
以下の範囲にあるカードを全て取っているはずです。なのでその範囲にあるカードの枚数を数えればよくて、ある座標範囲内にあるカードの枚数は二分探索などで求めることができます。
こうやって より上側のカードについて「どちらが取るか」を判定できるので、これが逆転するところがさきほど示したゾーンの境界になります。
大量クエリの高速処理を考える
これで答えを求めるための道筋は見えました。あとは計算量です。
答えを求めなければいけない がたくさんあるので、結局は「
が与えられたときに高速にゾーンの境界を求められるか?」という話になります。これを解決する方法は2つあります。
の値が数直線の右側に移動すると、ゾーンの境界も右側に移動していくこと(単調性)を利用する。与えられた
をソートし、しゃくとり法で境界を求めていく。
- さきほどの「どちらが取るか」自体に単調性があることを利用し、これを二分探索する。
これはどちらでも良いです。計算量オーダーとして優位なのはしゃくとり法ですが、各クエリを独立に処理できたほうが分かりやすいので計算時間に余裕があれば二分探索でも良いでしょう。
境界が分かった後は、各ゾーンの累積和で答えを求めます。交互に取るゾーンがあるところも考慮し、1つ飛ばしの累積和(添字の偶奇ごとに累積和を取ったもの)も求めておくと良いです。
ACコード
- (C++、しゃくとり)Submission #3988902 - AISing Programming Contest 2019
- (C++、二分探索)Submission #3996155 - AISing Programming Contest 2019
E - Attack to a Tree
解法
木DPの着想を得る
ある適当な点を根とする根付き木とみなし、葉から順番に値を計算していく木DPを考えてみます。
DPテーブルが持つ情報として必要そうなものは、「その頂点以下で何本の辺を切ったか」「その頂点を含む連結成分の、現時点での電力合計」です。このうち電力合計はとても大きい値になり得ますが、切った辺の本数は最大でもその頂点以下にある辺の本数なので比較的少ないです。そこで
= 頂点
以下の部分木を考えたときに、辺を既に
本切っているときの、頂点
を含む連結成分の電力合計の最小値。ただし、辺を切ったことで既に確定している連結成分は問題の条件を満たしていなければならない。
と定義します。電力を足りなくさせることが目的、つまり電力合計をなるべく小さくしたいので最小値を取っています。
ただしこのままでは情報が不足しています。各連結成分が満たすべき条件は、「連結成分にコンピュータが存在しない」「連結成分内の電力合計が負」のどちらかなので、電力合計だけでなくコンピュータが存在するかどうかの情報が必要になってきます。そのため、
= 頂点
以下の部分木を考えたときに、辺を既に
本切っていて、部分木内にコンピュータが存在する(
)/しない(
)ときの、頂点
を含む連結成分の電力合計の最小値。ただし、辺を切ることで既に確定している連結成分は問題の条件を満たしていなければならない。
と各頂点が持つ値を定義します。以下はある状態において、各添字がどのようになるかを示す一例です。
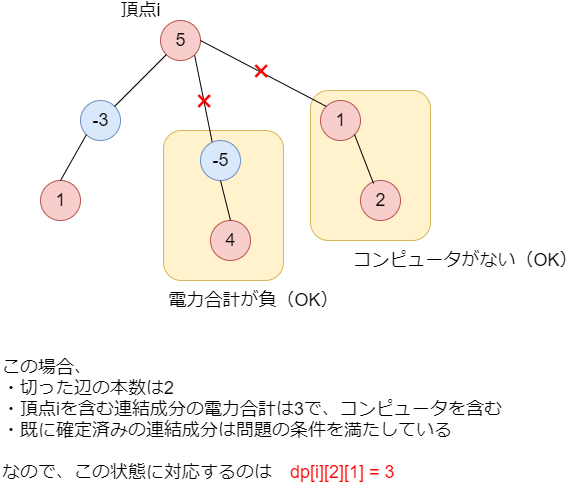
これなら、後に示すように遷移を構成することができます。
遷移を考える
子の情報から親の情報へ、どのようにDPの遷移を作ればよいか考えてみます。
イメージとしては、最初は親を要素数1の部分木として考え、そこに子の部分木を1つずつマージしていきます。親と子それぞれについて、さきほどの についてループを回します。
このとき、子からの辺を繋ぐか切るかという2通りが考えられます。
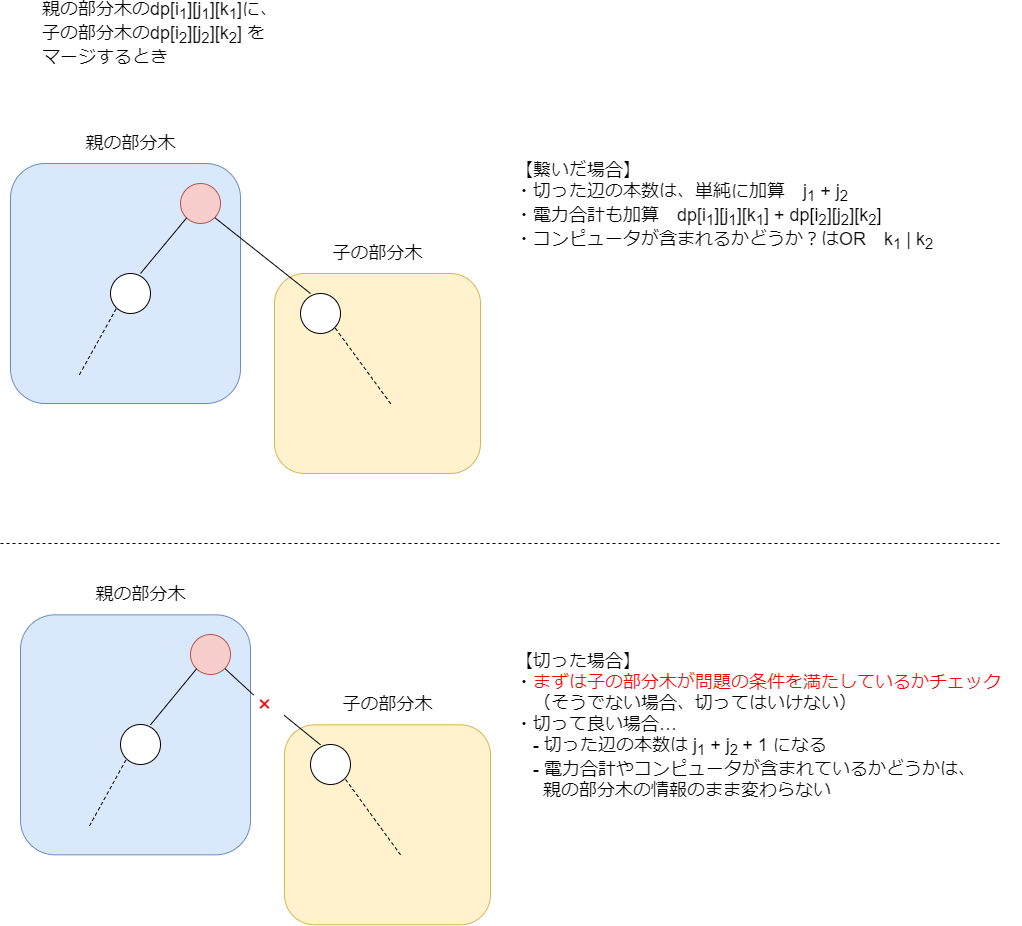
添字が多いので式がややこしくなりがちですが、
- 辺を繋ぐ場合、今までに切った辺の数・電力合計は加算し、コンピュータがあるかどうかはOR演算する。
- 辺を繋がない場合、まずは子の部分木が条件を満たしているかどうかをチェック! 満たしている場合は、切った辺の数は合計に1を足したものになり、それ以外の情報は親の情報がそのまま残る。
という風に遷移先を求めることができます。この遷移先に対して「今の値より値が小さくなるなら更新」と操作することを繰り返すと遷移ができます。
計算量について、通称「二乗の木DP」
さきほどのDP、子をマージするたびに親子それぞれの切った辺の数についてループを回すので計算量がひどくなりそうな気がします。具体的には全頂点について辺の数の2乗ループを回しているので、全体 になりそうです。
ですが、「その時点で持っている部分木のサイズまでしかループを回さない」という実装をすることで、全体計算量を とすることができます。これが通称「二乗の木DP」 と呼ばれるものです。部分木の辺の数は頂点の数-1なので、切った辺の数でループする場合はこのテクニックが使えます。
ACコード(&実装について)
私の実装について少し補足です。
DPテーブルに持つ値についてですが、 という値を使っています。先ほど書いたようにこのテーブルの中には添字で定義された状態における電力合計の最小値が入っていますが、ときには「そのような添字に対応する状態が存在できない」ということがあります。一番単純な例では、部分木内にコンピュータが1つもない場合は
に対応する状態はありません。このようなときには値に
を入れています。
この問題ではDPを回した後、最後に「辺の切り方が合計 本であるような、問題文の条件を満たす分け方が存在するか」を根について調べて、一番小さい切断本数を答えることになります。このときに「
の場合はそのような状態が存在しない」という決めごとをしておくと判定を正しく行うことができます。コードでは以下の部分です。
for(int n=0; n<N; n++){ if(dp[0][n][0] < INF) ans = min(ans, n); if(dp[0][n][1] < 0) ans = min(ans, n); }
Hello 2019 (Codeforces) 参加記録&解説(A~D, F)
2019年最初のコンテストはABCDFの5完で111位!幸先いいですね。

A. Gennady and a Card Game
問題概要
2文字の文字列でトランプのカードを表す。1文字目がランク、2文字目がスートに対応する。
場にあるカードが与えられ、さらに5枚の手札が与えられる。場にあるカードに対して、ランクまたはスートの少なくとも一方が一致するカードをプレイすることができる。
手札の中にプレイできるカードがあるかどうか判定せよ。
制約
省略
解法
手札を順に場のカードと比較し、1文字目または2文字目が一致するものがあるかを判定すればよいです。
ACコード
B. Petr and a Combination Lock
問題概要
個の角度
が度数法で与えられる。それぞれの角度に対して左回り/右回りを自由に選んで、1周あたり360度のダイヤルを回す。操作が全て終わった時にダイヤルが最初と同じ位置にあるような回し方が可能であるかどうか判定せよ。
制約
解法
左回りをプラス、右回りをマイナスとして角度を符号付きで全て合計したときに、その値が360度の倍数になっていればよいです。
制約より が十分間に合うので、回す方向を全探索してそれぞれ計算すればよいです。
ACコード
私の実装はbit全探索です。hackを狙ってコードを読んでいたら、再帰関数での実装も多く見られました。
C. Yuhao and a Parenthesis
問題概要
括弧だけで構成された文字列が 個与えられる。文字列2つをペアにして正しい括弧列をできるだけ多く作りたい。1つの文字列が2つ以上のペアに属することはできない。
作ることができるペアの最大数を求めよ。
制約
- 全ての文字数の合計は
を超えない
解法
正しい括弧列の条件は、( を+1、) を-1とする累積和を取ったときに、
- 文字列全体の合計がちょうど0である。
- 頭から見て、どの時点でも累積和が0以上である。
を満たすことです。
このことを考えると、2つの文字列をペアにして正しい括弧列とするためには、ある非負整数 に対して
- 前半の文字列
- 合計が
である。
- 頭から見て、どの時点でも累積和が0以上である。
- 合計が
- 後半の文字列
- 合計が
である。
- 頭から見て、どの時点でも累積和が
以上である。
- 合計が
をそれぞれ満たす必要があります。
あとはそれぞれの文字列に対して累積和の最小値と合計を計算して、「合計が で、最小値の条件を満たすものの個数」を整数
ごとに集計します。その値を
とすると、正整数
について正しい括弧列は
個作れます。合計0の文字列は合計0の文字列とペアになるので、
個作れます。これらを全て加算すれば答えが求められます。
ACコード
D. Makoto and a Blackboard
問題概要
整数 の初期値を
とする。整数
に対して、以下の操作を
回行う。
- その時点での
の約数の中からランダムに1つ選ぶ。どの約数が選ばれる確率も等しいものとする。
をその約数で置き換える。
操作が終わった後の の値の期待値を求めよ。答えは有理数となるため、その値を既約分数
としたときの
の値を出力せよ。
制約
解法
「約数を等確率で1つ選ぶ」という操作をしたときに、 のそれぞれの素因数の個数がどうなるか考えます。
にある素因数
が
個含まれているとすると、操作後の素因数
の個数は
個の中から等確率に1つ選ばれると考えることができます。そしてこの事象は素因数ごとに独立であるとみなすことができます。
そのため、まず を素因数分解してしまい、素因数ごとに考えます。ある素因数
についてだけ注目すると、「
回操作後に素因数
が
個含まれている確率」を
とするようなDPを考えることができます。
遷移は、 に
を掛けたものを
に加算することで計算できます。「
回の操作後に素因数
が
個含まれている確率」、すなわち
を以降
と表記します。
これを全ての素因数について計算すると、全ての の約数について
が最後にその数になっている確率を計算できます。ちょっと数式がごちゃごちゃするので、仮に
の相異なる素因数が
の2種類だとして、それぞれの個数を
とします。
このとき の約数は
と表現できて、最後にその数が残る確率は
となります。求めたいのは期待値なので、
を全て合計すればよいです。
これらを約数ごとに全て計算してもよいですが、さらに簡単にする方法があります。求めたい値は を全ての
と
の組み合わせについて合計したものですが、これを分配法則を使ってまとめると
という形になり、 と
を完全に分離できます。そのためそれぞれで値を求めておいて、最後に掛け算する方法でも期待値を求めることができます。
ここまでの話は素因数の種類数が2個でない場合でも成り立ちます。それぞれの素因数ごとに値を求めて全部掛け算すればよいです。
ACコード
- (分配法則不使用)Codeforces
- (分配法則使用)Codeforces
分配法則使用コードのほうが圧倒的にシンプルなのでオススメです。
F. Alex and a TV Show
問題概要
までの番号が付けられた多重集合がある。始めはどの集合も空である。
以下の4種類のクエリを 個処理せよ。
1 x v番号の集合を
1つだけの集合に置き換える。
2 x y z番号の集合を、番号
の集合の和集合に置き換える。
3 x y z番号の集合を、番号
の集合の「直積集合」に置き換える。ただしここでは要素同士の組の代わりに、それらの要素の最大公約数を直積集合の要素とする。
4 x v番号に含まれる要素
の個数の偶奇を出力する。
制約
- クエリ1, 4について、
解法
それぞれの集合の状態として、単純に各値の個数や偶奇を持っていてはクエリの処理が間に合いません。特に最大公約数を求める処理が厄介なので、これを処理しやすいような状態の持ち方を考える必要があります。
状態 を、「集合
に含まれる要素のうち、
を約数に持つ要素の個数の偶奇」とするような状態を持ちます。このときクエリ2は
ごとに要素数を足せば良いので、偶奇をビットで管理している場合はXORで計算できます。
またクエリ3の結果 を約数に持つ要素の個数は、集合
それぞれで
を約数に持つ要素の個数の積になります。そのためビットで管理している場合はANDで計算できます。
クエリ1は単純に の約数全てのビットを立てたものに置き換えれば良いので、これでクエリ1, 2, 3の処理が効率的にできることが分かりました。あとは肝心のクエリ4です。
このクエリを処理するためには、「 を約数に持つ要素の個数の偶奇
」から「
の個数の偶奇」を求める必要があります。これは包除原理を用いて求めることができて、結論を書くと
の倍数であり、
と表現できるような
について、
が同じ素因数を2つ以上含むなら(つまり、1より大きい平方数を約数に持つなら)無視
- そうでない場合、
に含まれる素因数が偶数個なら、+1倍
に含まれる素因数が奇数個なら、-1倍
したものをすべて足すと求めることができます。ただし今回は偶奇を表すビットなので、+1倍と-1倍を区別する必要はありません。
この証明はちょっと面倒なので書きませんが…AtCoderの 「LCM Rush」の解説、またその問題などを扱っているtsutajさんの包除原理まとめPDFなどが参考になると思います。
これでクエリ4の解を求めることができます…が、計算量を確認すると となり単純計算で70億。全てのクエリをbitsetを用いて高速に処理できるよう前計算などをしておくことで、何とか間に合います。キツいですね。
ACコード
AGC030 B - Tree Burning
今回は私自身がAB2完で実質的にこの1問しか解説を書けないのと、この1問だけでかなり説明が長くなりそうなので、単独記事にします。
Twitter見ていると微妙に色々違う解法があるようで…?私が本番で考察した内容をベースに書きます。他の人が書いていることとズレがあるかもしれないので、そこはご注意ください。
はじめに
以降の説明で使う方向を定義しておきます。高橋くんの家を円の上側に置き、問題文の座標と同じ反時計回りの向きを「左」、その逆向きを「右」とします。
また説明を簡単にするため、与えられる木の座標値 とは別に、座標の測り方を逆にして、逆向きに回った時に
番目にある木の座標値
を定義しておきます。これらは同じ木をどちら側から訪れるかによって2通りの座標値を付けているだけであることに注意してください。
具体的には で計算できます。
も
も木の位置を1-indexedで扱い、
としておきます。
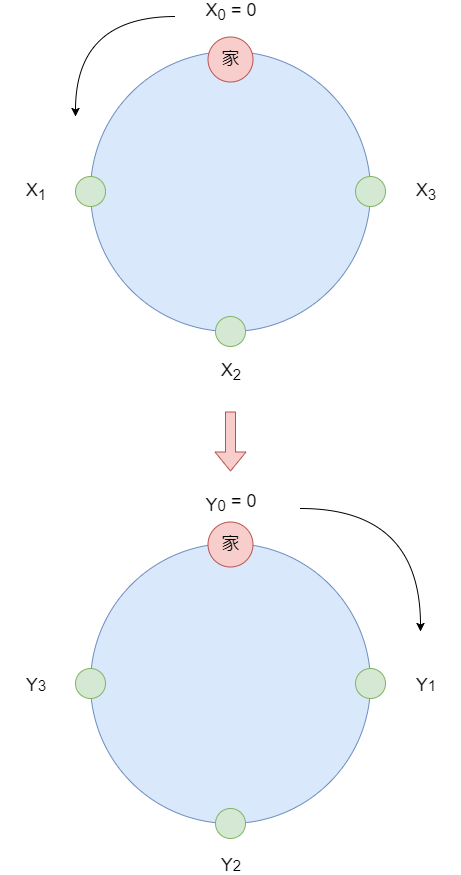
部分点解法
まず部分点ですが、DPをします。「家から左に 本、右に
本の木を訪問済みで、最後に訪れたのが左側の木なら
、右側の木なら
であるときの最大移動距離」を
とします。
このようにDPの状態を定義すると、左右合計で 本の木を訪れた時点で終わりなので、
を
および
の範囲で全て求めたもののの最大値が答えになります。家の座標を
としているので、初期条件は
です。
遷移を考えます。 は左に
本、右に
本の木を訪問済みで、最後に左側
の木を訪れている状態です。ここからは2通りの移動ができて、
- さらに左に進み、
の木を訪れる。加算される移動距離は
で、
に遷移する。
- 向きを変えて右に進み、
の木を訪れる。加算される移動距離は
で、
に遷移する。
という遷移になります。

からの遷移も同様に考えることができます。このDPを回すと
で計算が終わり、部分点を取ることができます。
部分点獲得コード
- (配るDP)Submission #3900997 - AtCoder Grand Contest 030
- (貰うDP)Submission #3893900 - AtCoder Grand Contest 030
DPの実装における違いとして、いわゆる「貰うDP/配るDP」というものがあります。本番中の実装は「貰うDP」でしたが、「配るDP」のほうが文章化しやすかったので今回の説明は「配るDP」で書いています。この問題はどちらで解いても大差ないです。
あと、 とか実際に要らないところまで回してしまっているのですが、まあ計算時間が約2倍になるだけで十分間に合うので…添字の演算を増やしてつまらないバグを混入させたくないので、私はコンテスト本番だとこういう実装をたまにやります。
満点解法
満点解法は、どのような動きが最適になるのかをある程度考える必要があります。とはいえ、全探索できるものは全探索します。
私の解き方では、
- 左側/右側に移動して訪れる木がいくつあるか(
通り)
- 最初に左右どちらに移動するか(2通り)
- 最後に左右どちらに移動するか(2通り)
を全探索しています。これら全部の組み合わせは 通りです。以降、これらを何か1つに固定したものを「パターン」と書くことにします。
左右に訪れる木の本数を固定すると、そこで円周を切り開くことができます。円周だと図も描きにくいので、以降は直線で考えていきます。

以降、左右それぞれへの「移動回数」というものを考えます。これは一度その向きへの移動を始めてから、折り返すか止まるまでを1回とします。例えば上の図では、左の移動回数が3回、右の移動回数が2回です。移動は未訪問の木に向かって行うので、左右ともに移動回数が木の本数を超えることはできません。
最初と最後の移動の向きを決めると、それによって左右の移動回数の「差」が決まります。例えば最初も最後も左だった場合、先ほどの例のように左に移動する回数は右に移動する回数より1回多いです。最初と最後の移動の向きが異なる場合、左右の移動回数は同じです。
パターンを1つ固定すると、左右にいくつ木があるかが決まり、左右の移動回数の差も決まります。これらが決まると、左右の移動回数の最大値を求めることができます。
移動距離を稼ぐにはなるべく多くの回数折り返したほうが得なので、この最大値を満たすように移動するのが良いです。またなるべく遠い位置で折り返したほうが距離を稼げるので、左右それぞれについてスタート地点から遠い木を折り返し地点として選びます。結果として移動の経路は以下のようになります。
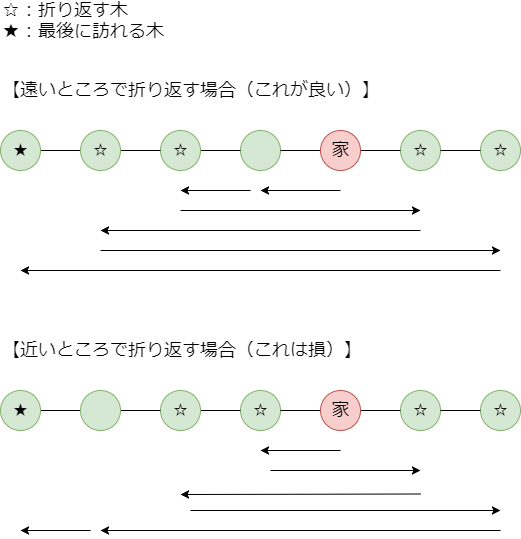
このような移動の合計距離は以下のように計算できます。
- 左右それぞれ、移動回数と同じ本数だけ外側から木を選び、スタート地点からその木までの距離を2倍(往復分)したものを全て合計する。
- その後、最後に訪れる木だけはスタート地点から片道だけの距離しかないので、片道分の距離を引く。
これがこの固定パターンにおける最適値です。この計算で必要なのは それぞれの「連続する要素の和」なので、累積和を用いれば1パターンあたりは
で計算できます。
これを パターン全部試して最も良いものを答えとします。全体計算量が
となり、満点を取ることができます。
満点獲得コード
Submission #3895457 - AtCoder Grand Contest 030
コードでは
- 左側に移動して訪れる木の本数を
dとする k1 == 0のとき、最初に左側に移動するk2 == 0のとき、最後に左側に移動する
という3変数で各パターンを全探索しています。
また、cx, cy がそれぞれ左右の移動回数の最大値です。移動回数の差を処理するために変なことをしていますが、普通にif場合分けで十分だと思います…