AGC030 B - Tree Burning
今回は私自身がAB2完で実質的にこの1問しか解説を書けないのと、この1問だけでかなり説明が長くなりそうなので、単独記事にします。
Twitter見ていると微妙に色々違う解法があるようで…?私が本番で考察した内容をベースに書きます。他の人が書いていることとズレがあるかもしれないので、そこはご注意ください。
はじめに
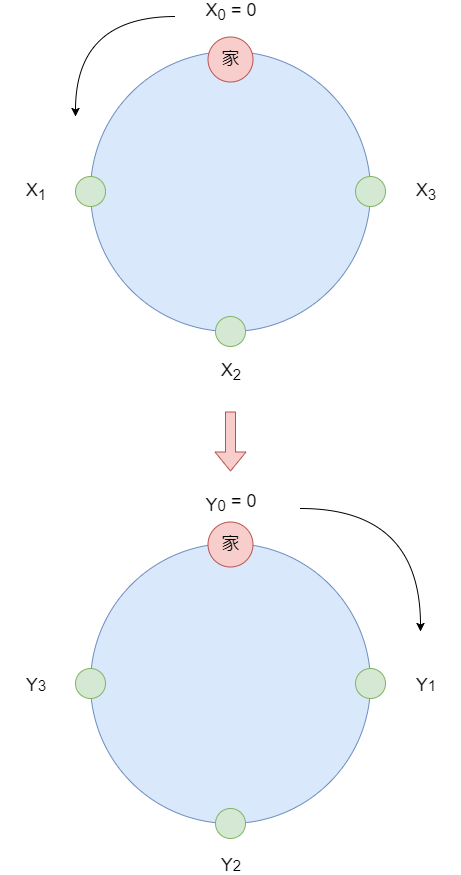
以降の説明で使う方向を定義しておきます。高橋くんの家を円の上側に置き、問題文の座標と同じ反時計回りの向きを「左」、その逆向きを「右」とします。
また説明を簡単にするため、与えられる木の座標値 とは別に、座標の測り方を逆にして、逆向きに回った時に
番目にある木の座標値
を定義しておきます。これらは同じ木をどちら側から訪れるかによって2通りの座標値を付けているだけであることに注意してください。
具体的には で計算できます。
も
も木の位置を1-indexedで扱い、
としておきます。
部分点解法
まず部分点ですが、DPをします。「家から左に 本、右に
本の木を訪問済みで、最後に訪れたのが左側の木なら
、右側の木なら
であるときの最大移動距離」を
とします。
このようにDPの状態を定義すると、左右合計で 本の木を訪れた時点で終わりなので、
を
および
の範囲で全て求めたもののの最大値が答えになります。家の座標を
としているので、初期条件は
です。
遷移を考えます。 は左に
本、右に
本の木を訪問済みで、最後に左側
の木を訪れている状態です。ここからは2通りの移動ができて、
- さらに左に進み、
の木を訪れる。加算される移動距離は
で、
に遷移する。
- 向きを変えて右に進み、
の木を訪れる。加算される移動距離は
で、
に遷移する。
という遷移になります。

からの遷移も同様に考えることができます。このDPを回すと
で計算が終わり、部分点を取ることができます。
部分点獲得コード
- (配るDP)Submission #3900997 - AtCoder Grand Contest 030
- (貰うDP)Submission #3893900 - AtCoder Grand Contest 030
DPの実装における違いとして、いわゆる「貰うDP/配るDP」というものがあります。本番中の実装は「貰うDP」でしたが、「配るDP」のほうが文章化しやすかったので今回の説明は「配るDP」で書いています。この問題はどちらで解いても大差ないです。
あと、 とか実際に要らないところまで回してしまっているのですが、まあ計算時間が約2倍になるだけで十分間に合うので…添字の演算を増やしてつまらないバグを混入させたくないので、私はコンテスト本番だとこういう実装をたまにやります。
満点解法
満点解法は、どのような動きが最適になるのかをある程度考える必要があります。とはいえ、全探索できるものは全探索します。
私の解き方では、
- 左側/右側に移動して訪れる木がいくつあるか(
通り)
- 最初に左右どちらに移動するか(2通り)
- 最後に左右どちらに移動するか(2通り)
を全探索しています。これら全部の組み合わせは 通りです。以降、これらを何か1つに固定したものを「パターン」と書くことにします。
左右に訪れる木の本数を固定すると、そこで円周を切り開くことができます。円周だと図も描きにくいので、以降は直線で考えていきます。

以降、左右それぞれへの「移動回数」というものを考えます。これは一度その向きへの移動を始めてから、折り返すか止まるまでを1回とします。例えば上の図では、左の移動回数が3回、右の移動回数が2回です。移動は未訪問の木に向かって行うので、左右ともに移動回数が木の本数を超えることはできません。
最初と最後の移動の向きを決めると、それによって左右の移動回数の「差」が決まります。例えば最初も最後も左だった場合、先ほどの例のように左に移動する回数は右に移動する回数より1回多いです。最初と最後の移動の向きが異なる場合、左右の移動回数は同じです。
パターンを1つ固定すると、左右にいくつ木があるかが決まり、左右の移動回数の差も決まります。これらが決まると、左右の移動回数の最大値を求めることができます。
移動距離を稼ぐにはなるべく多くの回数折り返したほうが得なので、この最大値を満たすように移動するのが良いです。またなるべく遠い位置で折り返したほうが距離を稼げるので、左右それぞれについてスタート地点から遠い木を折り返し地点として選びます。結果として移動の経路は以下のようになります。
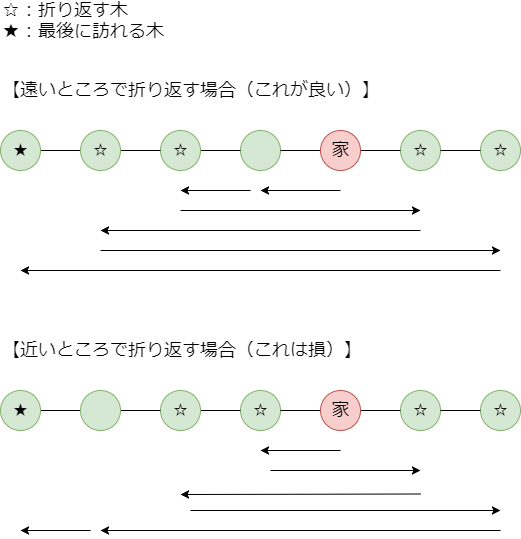
このような移動の合計距離は以下のように計算できます。
- 左右それぞれ、移動回数と同じ本数だけ外側から木を選び、スタート地点からその木までの距離を2倍(往復分)したものを全て合計する。
- その後、最後に訪れる木だけはスタート地点から片道だけの距離しかないので、片道分の距離を引く。
これがこの固定パターンにおける最適値です。この計算で必要なのは それぞれの「連続する要素の和」なので、累積和を用いれば1パターンあたりは
で計算できます。
これを パターン全部試して最も良いものを答えとします。全体計算量が
となり、満点を取ることができます。
満点獲得コード
Submission #3895457 - AtCoder Grand Contest 030
コードでは
- 左側に移動して訪れる木の本数を
dとする k1 == 0のとき、最初に左側に移動するk2 == 0のとき、最後に左側に移動する
という3変数で各パターンを全探索しています。
また、cx, cy がそれぞれ左右の移動回数の最大値です。移動回数の差を処理するために変なことをしていますが、普通にif場合分けで十分だと思います…