AtCoder Beginner Contest 170 F - Pond Skater

解法

1ターンに1マスの移動であればグリッド上のBFSで解けますが、今回は1ターンに $K$ マスまで動くことができます。これをそのままBFSで処理すると1つのマスから遷移可能なマスが最大 $4K$ 個になり、全体計算量 $O(HWK)$ になって間に合いません。

具体的にどのように無駄が生じているのかを、マスが一直線に並んでいるケースで見てみます。マス内の数値はスタートからの最短距離です。

f:id:betrue12:20200614225600p:plain

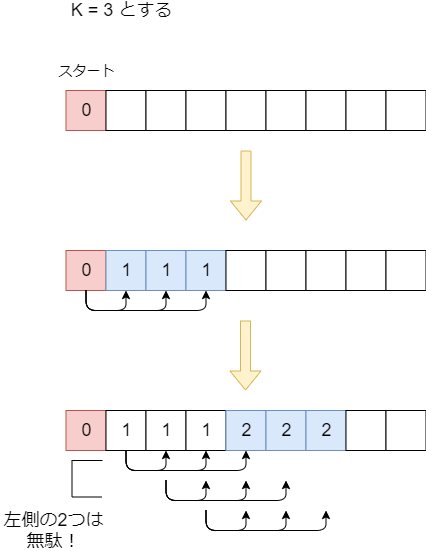
このように、同じターン数で自分より先を行っている経路を後から追うのは無駄です。これを除外するため、BFSに以下のような改良を加えます。

スタートからマス $(i, j)$ までの距離を $dist\lbrack i\rbrack\lbrack j\rbrack$ として、キュー等を用いたBFSを行う。
あるマスからの遷移として、4方向の移動をそれぞれ試す。決めた方向に対して、マス移動した先を順番に見ていく。
- このとき移動先のマス $(x, y)$ が、障害物、枠外、または $dist\lbrack x\rbrack\lbrack y\rbrack \le dist\lbrack i\rbrack\lbrack j\rbrack$ であるようなマスだった場合、その方向の遷移をそこで打ち切る。
- その上で、 $(x, y)$ が未訪問マスであった場合は $dist\lbrack x\rbrack\lbrack y\rbrack = dist\lbrack i\rbrack\lbrack j\rbrack + 1$ としてキューに入れる。

このようにすると、先ほどの無駄な移動は打ち切られます。

この解法の正当性確認と計算量評価をしましょう。正当性は、「 $dist\lbrack x\rbrack\lbrack y\rbrack \le dist\lbrack i\rbrack\lbrack j\rbrack$ であった場合、打ち切らずに $(i, j)$ からの遷移を考える代わりに、 $(x, y)$ からの遷移をすることでより良い遷移ができる」ことから言えます。より良い遷移とは具体的には、より遠くのマスまで届いてかつ $dist$ の値が同じかより小さい、という意味です。

計算量については、あるマスに対して遷移で入ってくる回数を考えると分かります。入ってくるけどそこで打ち切られるような場合を除くと、あるマスに入ってくる回数は各方向あたり高々1回ずつです。具体的にはそのマスにある方向から流入可能なマスのうち、 $dist$ が最も小さく、かつ $dist$ が同じものの中では最も近いものからしか流入しません。

よって、方向数 $4$ を定数と見なせば「打ち切られ」以外の遷移回数は合計で $O(HW)$ 。打ち切られる回数の合計も（今度は遷移元に注目すると）マス数×方向数で $O(HW)$ です。よって全体計算量 $O(HW)$ となり間に合います。