Codeforces Round #636 (Div. 3) F. Restore the Permutation by Sorted Segments

Problem - F - Codeforces

問題概要

長さ $n$ の順列 $p_{1}, ..., p_{n}$ がある（与えられない）。この順列に対して、 $r=2, ..., n$ それぞれに対して以下のように計算される $n-1$ 個の数列が与えられる。

各 $r$ に対して、 $l \lt r$ なる $l$ を選び、 $p_{l}, ..., p_{r}$ をソートした数列。

ここで $n-1$ 個の数列は並べ替えられた順番で与えられる。

この与えられる $n-1$ 個の数列と矛盾しないような順列 $p_{1}, ..., p_{n}$ を1つ求めよ。そのような順列が1つ以上存在することは保証される。

制約

マルチテストケースであり、ケース数 $t \le 100$
各ケースについて $2 \le n \le 200$ であり、全ケースの $n$ の合計は $200$ を超えない
与えられる数列は上記の条件を満たし、解が1つ以上存在する

解法

正解の順列と与えられる数列の位置関係を図示すると、例えば以下のようになっています。

f:id:betrue12:20200422145338p:plain

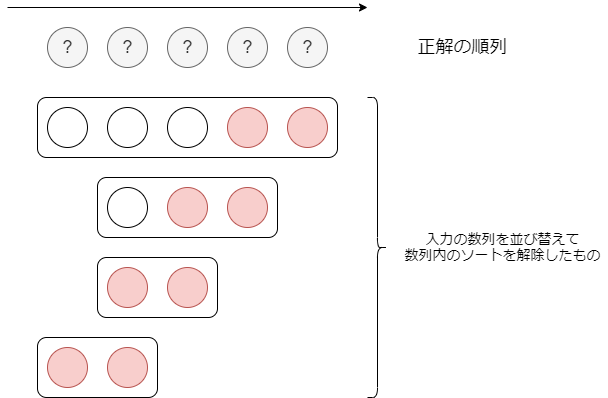
各数列の長さはテストケースに依りますが、赤丸の位置は必ず存在します。

実際には入力の数列のうちどれがどの位置に対応するのかも、各数列の中身が元々どう並んでいたのかも分かりません。なのでこれらに依存しない情報である、「 $1, ..., n$ の各値が入力の数列に合計何回登場するか」に注目します。すると

目標の順列で末尾にある値は、必ず登場回数が1回である。
目標の順列で末尾でも先頭でもない値は、必ず登場回数が2回以上である。

ということが言えます。

そのため登場回数が1回であるような値は1種類または2種類であるはずです。このうち1つを正解の順列の末尾にある値だと仮定することにします。

この末尾の値が含まれている数列について、その中にある値の登場回数をそれぞれ減らします。そうすると正解の順列で末尾から2番目にある値の登場回数が1回になります。

f:id:betrue12:20200422145847p:plain

これで登場回数1回になる値を採用して、その値が含まれている数列について各値の登場回数を減らして…を繰り返したいところですが、上図のように先頭の値も途中で登場回数が1回になる可能性があります。このように処理の途中で2択を迫られると面倒です。

そのため最初の時点で、正解の順列の末尾の値（高々2通り）と先頭の値（末尾以外の $n-1$ 通り）を決め打ちしてしまいましょう。そうすると、各ステップでは「登場回数が1回になった値のうち先頭の値でないもの」を選べばよく、これは高々1種類です。

1回のシミュレーションを $O(n^{2})$ や $O(n^{2}\log n)$ などで行うことができれば実行時間としては間に合います。これでシミュレーションを進め、途中で値の候補がなくなったり、構築できても条件に矛盾するような場合はハズレです。最後まで順列を構築できてかつ全ての条件を満たせば、それを出力して終了します。