AtCoder Beginner Contest 162 F - Select Half

お題箱より。

前置き

リクエストでは「そもそもなぜDPを思いつくのか」を知りたいという声をもらったのですが…この点は非常に難しいと思っています。というのも、私の場合はDPで最終的に解けない問題であっても考察途中で「DPできないか？」ということを考えているからです。同じように「貪欲できないか？」「二分探索できないか？」なども多くの問題で考えます。

どちらかというと「仮にDPに落とし込んだとしたらどういう状態が持てるだろう？」と考える習慣を付けるのがオススメです。思いつかなかったり、計算量的に間に合わないDPしか思いつかないなら一旦他の方針に頭を切り替えて良いです。それがたとえハズレ方針であっても、考察の引き出しを増やしてその中から適切な方針を選ぶ力に繋がります。

実際に私はこの問題で、最初にDPではない方針を考えて途中まで実装もしてしまっていました。結果的にタイムロスになりましたが、「こっちの解法ではダメ」という理由も含めて理解できたので後でDPにしっかり切り替えられたと思います。「試しに仮説を立てて考えてみる」ことがとても大事です。

解法

数列に対するDPで最も基本となるのは「左から順に見ていく」DPです。今回は要素を選ぶ条件として「個数」「選んだ要素同士の間隔」が制限されているため、これらを判断できるような情報をDPテーブルに盛り込みます。例えば以下のようなものです。

$dp\lbrack i \rbrack\lbrack j \rbrack =$ 最後に選んだ要素が $a_{i}$ であって、選んだ個数が $j$ 個であるときの、選んだ要素の和の最大値

これは間に合わないので、この問題の性質を使って改良しましょう。

実際に数を並べて、問題の条件を満たすように要素を選ぶ方法をいくつか考えてみます。必ず1つ間隔を空けるというルールでだいたい半分の要素を選ぶので、ほとんどの場所では「ちょうど1個」間隔が空いていることになります。そして1個より多く間が空いているところはそんなにたくさん作れません。

選ぶ位置と選ばない位置をボールのように図示すると、具体的には以下のようになります。

f:id:betrue12:20200422235344p:plain

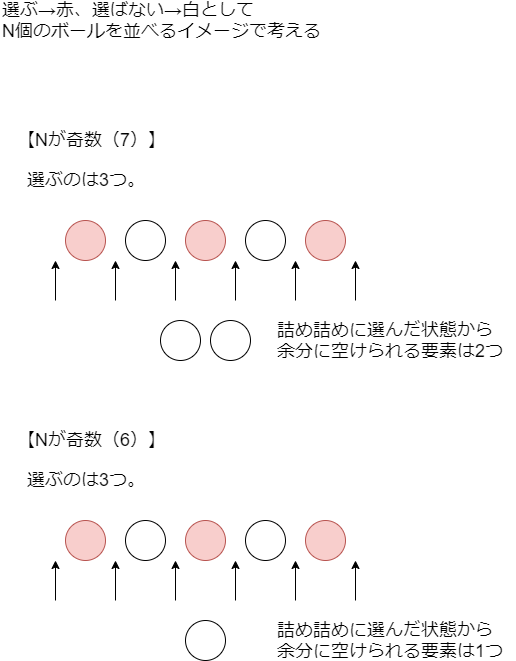
つまり先ほど試しに立てたDPで

$dp\lbrack i \rbrack\lbrack j \rbrack =$ 最後に選んだ要素が $a_{i}$ であって、選んだ個数が $j$ 個であるときの、選んだ要素の和の最大値

としましたが、実際に起こり得る状況ではこの $j$ はほぼ $\frac{i}{2}$ に近い値になって、例えば $dp\lbrack 100 \rbrack\lbrack 0 \rbrack$ とか $dp\lbrack 100 \rbrack\lbrack 99 \rbrack$ みたいな値は考えなくていいということが分かります。これが公式解説で言う「無駄」の意味です。

では何を持てば良いかというと、旧DPの $j$ が $\frac{i}{2}$ に近いことを利用し、その誤差を意味するような値を持てば良いです。今回は先ほどの図で記した「詰め詰めの状態に比べて余分に空けた要素数」を持つことにします。

$dp\lbrack i \rbrack\lbrack j \rbrack =$ 最後に選んだ要素が $a_{i}$ であって、詰め詰めの状態に比べて余分に空けた要素数が $j$ 個であるときの、選んだ要素の和の最大値

この場合は $j$ として2以下の値しか考えなくて良いので、状態数が少なくなります。

$dp\lbrack i \rbrack\lbrack j \rbrack$ からの遷移を考えます。 $a_{i}$ の次に $a_{i+2}$ を取るのは「詰めている」状態なので、 $dp\lbrack i+2 \rbrack\lbrack j \rbrack$ に遷移。 $a_{i+3}$ を取ると「1個余分に空けた」状態なので $dp\lbrack i+3 \rbrack\lbrack j+1 \rbrack$ に遷移…という風に考えれば良いです。

端の要素を空ける場合の処理などが少し面倒ですが、この考え方でDPを組むことができます。

今回の問題では「1個以上間隔を空けておよそ半分の要素を選ぶ」という制限がけっこう強いものであり、あまり好き勝手に要素を選べないことを利用して、状態数の少ないDPを考えることができました。一度間に合わないDPを考えてから「無駄」に気付くか、先に考察を進めてからDPに落とし込むか。どちらが先でも良いですが、「DPできないかな？」と「何か良い性質無いかな？」という2つの視点が必要です。引き出しを増やし、どんどん仮説を立てて問題を解いていきましょう。