AtCoder Beginner Contest 178 F - Contrast

解法が色々ある問題。シンプルで実装も楽な解法1と、私が本番で解いた解法2を証明付きで紹介します。前者のほうが断然オススメ。

解法1

まず $A, B$ 合計で $N$ 個を超える値が存在する場合、どのように並べても $A_{i} = B_{i}$ となる箇所が存在してしまいます。この場合は No を出力して終了します。以降は、どの値の登場数も $A, B$ 合計で $N$ 個以下であるとします。

突然ですが $B$ を反転させて降順ソート状態にします。この状態で $A$ と $B$ を並べてみると、 $A_{i} = B_{i}$ となっている値は高々1種類だけであることが言えます。もし2種類以上の異なる値がそれぞれ同じ位置にある場合、それらは $A$ と $B$ において同じ位置関係で並んでいるということになり、「片方は昇順、片方は降順」という前提に反するからです。

$A_{i} = B_{i}$ となっている値が存在しない場合はこの $B$ が答えです。もし $A_{i} = B_{i}$ となっている値が存在する場合、その値を $x$ として、 $A_{i}$ も $B_{i}$ も $x$ でないような両端の領域を探します。この領域内の $B_{i}$ と、 $x$ が被っているところの $B_{i}$ を1つずつ組にしてスワップしていけば完成です。スワップする両者の位置はどちらも「 $A_{i}, B_{i}$ のうち片方は $x$ で、もう片方は $x$ でない」という状態になるのでこれで条件を満たします。

f:id:betrue12:20200914232651p:plain

この両端の領域の要素数が、 $x$ が被っている領域の要素数以上であることを示します。上の図のように長さ $a, b, c, d, e$ を定めると、

図より、 $a+b+c+d+e = N$
$x$ の登場数が合計で $N$ 個以下であることから、 $b+2c+d \le N$

であるので、不等式を変形することで $a+e \ge c$ を示すことができます。以上でこの構築の正当性が証明されました。

ACコード1

Submission #16762957 - AtCoder Beginner Contest 178

解法2

$A, B$ 合計で $N$ 個を超える値が存在する場合は No である、という点は同じです。

$A$ も $B$ も並び替えができる、と想定して解きます。最後に出力する時に、 $A$ の各要素が元々並んでいた位置に合わせて対応する $B$ の要素を並べれば良いです。

各値について $A, B$ それぞれの出現数を調べます。そして以下の図に示すように、 $B$ のほうが多い値を左側に、 $A$ のほうが多い値を右側に、同じ順序で $A, B$ ともに並べ替えます。そして各値について「 $A$ と $B$ についてその値が被っている長さ」を調べ、その長さだけ $B$ を右に巡回シフトすれば完成です。

f:id:betrue12:20200914225731p:plain

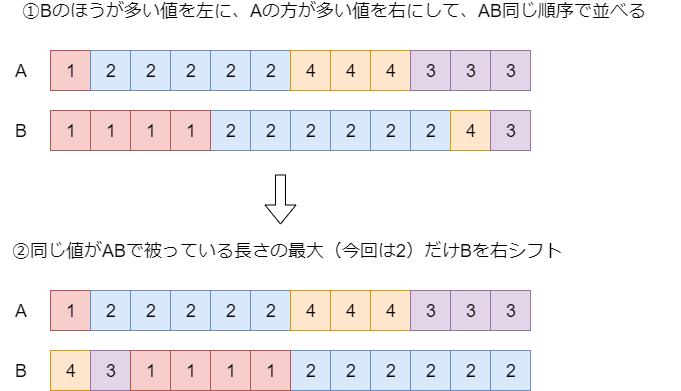
この解法の正当性を証明します。左にある値から順に見ていくと、 $B$ の方が多い値を全部先に使っているので、各値を入れる前後では常に $B$ の要素数のほうが多く（または等しく）なっています。より具体的には、全ての値について

（その値が $A$ に登場する左端） $\le$ （その値が $B$ に登場する左端）
（その値が $A$ に登場する右端） $\le$ （その値が $B$ に登場する右端）

が成立しています。図の①のほうの状況です。

この状態で被っている長さが最大であるような値を $x$ とします（図では青く塗っている $x=2$ が $2$ つ被っています）。その長さだけ $B$ を右シフトすると、全ての値について元々被っていた領域は切断されて被らなくなります。また1周して $B$ 側の右端と $A$ 側の左端がくっつくこともありません。 $x$ 以外の値が1周してくっつくためには $x$ が被っていた領域を超える必要があり、これは無理です。また $x$ についても、その登場数が合計 $N$ 個以下であることからあり得ません。