AGC029 参加記録&解説(A~D)
AtCoder Grand Contest 029 - AtCoder
今回は4完!完答数で言うと自己ベストです。配点が低めでペナルティ込みの時間がかなり遅いので、パフォーマンスはそんなに高くないですが…

A~Dを振り返ります。
A - Irreversible operation
解法
この操作は「白石を1つ左にずらす」という操作に相当します。これ以上ずらせない、すなわち「白白白...白黒黒黒...黒」のような状態になるまで操作を繰り返すことができます。
この状態にするまでの操作回数を考えましょう。左端を0とする座標をとって「白石の座標値の合計」を考えると、白石を左に1つずらす操作を1回するたびにこの値は1減ります。そのため、
- 操作前の白石の座標合計:与えられた入力をもとに計算
- 操作後の白石の座標合計:白石を
個とすると
をそれぞれ計算して、これらを引き算すると答えが出ます。
もしくは、この値は「転倒数」とみなすことができるので、転倒数を求める要領で左から計算する方法もあります。この場合は初期状態の各白石について「それより左側にある黒石の個数」を数えて全部足し算すればよいです。どちらでも で計算できます。
ACコード
- (Ruby、合計の差)Submission #3805088 - AtCoder Grand Contest 029
- (Ruby、転倒数)Submission #3793082 - AtCoder Grand Contest 029
B - Powers of two
解法
結論を言ってしまうと「大きい方からペアの候補を探していってマッチングを作るのが最適」となります。これを証明します。
まず、与えられた数のうち一番大きい値を取ってきてその値を とします。
とペアになる候補として
を取ったとして、和を
とします。
このとき であることから
です。そして作りたい2冪の値
のうち、この範囲に入っているものは1つしかないことが証明できます。隣り合う2冪の値の比は2ですが、
と
の比は2未満だからです。
そのため とマッチングできる数は1種類だけに定まります。このときマッチング相手がいるのに「マッチングをしない」という選択をしてしまうと、
は以降どの数ともマッチングができずに残るので
とマッチングできる候補
が
以外の値とマッチングできないとき、マッチングをしないのは単純に損である。
が
以外にマッチング相手を持っている場合、足し引き0になって損をしない可能性はあるが、得をすることはない。
と、マッチングをしないことに得がありません。マッチングが作れる場合は作ってしまうのが最適になります。
の次に大きい値を見るときには、同じようにこれを「一番大きい数」として考え、同じように処理して大丈夫です。たとえ
が残っていたとしても、その
はどの数ともマッチングできないので無視してよいからです。
これを全ての値について繰り返すと答えが求められます。「ペアになる候補の値が存在するか?」という判定が必要になるので、mapなどで各値の個数を管理するとよいですね。mapを使うと全体計算量は になります。
ACコード
C - Lexicographic constraints
解法
まずは二分探索することを考えます。文字の種類数 を固定し、「
種類の文字で与えられた条件を満たすことができるか?」のYes/No問題を考えます。
種類あれば絶対に条件を満たせるので、初期条件は
とすることができて、反復回数は
回です。以降、Yes/No問題を考えていきます。
最適な文字列の作り方を考える
番目の文字列を
と表記します。その長さは
です。
この次の文字列 は次のように作るのが最適です。
のとき、
の後に
を繋げたもの。
- 例:
、
とすると、
- 例:
のとき、
の
文字目までを「1つ繰り上げた」もの。
- 例:
、
とすると、
- 例:
「1つ繰り上げる」という操作は整数の桁の繰り上がりに似ていて、 で文字数が2の場合は
のような要領で繰り上がっていきます。
そのため発想として、「 種類の文字からなる文字列を
進数の整数のようにみなして繰り上がり等をシミュレートし、一番上の桁が溢れなければOK」というようにYes/No問題を解くことを考えます。
ただそのまま整数で実装すると 進数で
桁の値を考えないといけないので、多倍長整数でもとても無理です。これを工夫して実装する必要があります。
※下の方の桁ほど答えに影響しづらいので、私は本番では「ある長さ以上のところの変化は無視する」という方法で通してしまいました…64bit変数2つでなんちゃって多倍長を作り、 がだいたいギリギリ128bit整数になるくらいまで桁数
を取るとジャッジは通りますが、恐らくhack可能です。提出コードはこれです。
文字列の効率的な持ち方
どうするのかというと、文字列で言うと でない、つまり
進数でいうと
でないところだけの情報を持ちます。例えば
という文字列は、 でないところだけを
と表現したものを集めて
という風に持ちます。桁については一番最初の文字を1桁目、文字については を0文字目としています。
このように管理した文字列に対して、先ほどの操作をそれぞれどのように行えばよいかを考えます。
の後ろに、長さが
になるまで
をある個数追加する
は情報として持たなくて良いので、何もしなくてよい。
を長さが
になるまで削る。
の末尾を、インデックスが
以下になるまで削る。
を1つ繰り上げる。
- 整数の繰り上がりと同様に、末尾から順に「値が
になったらゼロにして1つ上の桁に1加算する」という処理を行う。
- 整数の繰り上がりと同様に、末尾から順に「値が
という風に各操作を行うことができます。
あとはこれを効率的に実現できるように の持ち方を考えます。単純にmapでもよいですし、末尾にしか操作をしないことに着目するとstackを用いてもよいです。
計算量について
ちょっと計算量の解析が面倒ですが、やってみます。以降、 とします。
まずは繰り上がり処理において、値を追加する回数の合計がどれくらいになるか?を考えます。繰り上がりが多く起こる場合というのは、例えば となっていて、その末尾に1加算するようなときです。
このような現象が頻繁に起こってしまっては計算量が多くなってしまいますが…今回の場合、 のような状態を「効率的に作る」ことができません。4桁目に1を足すという操作を地道に
回繰り返すことでしかこのような形は作れません。
一般的に言うと、 回の操作で
から始まって
(
桁)への繰り上がりが実現できます。この時各桁に値を追加する回数の合計は、
- 上から1桁目:1
- 上から2桁目:
- ...
- 上から
桁目:
となり、その和は です。これはおよそ操作回数
の
倍になっていて、つまり操作回数の2倍で抑えることができます。操作回数は合計で
回なので、値を追加する回数の総数も
で抑えることができます。
次に末尾の要素を削る処理です。要素を削るためには、それより前に要素が追加されている必要があります。先ほど見たように値の追加回数は で抑えられているので、削る回数の合計も
で抑えられます。
以上の考察によって、 に対して変更を加える回数の合計は
となります。もしstackを使っていれば1回の変更は
、そして二分探索の反復回数が
なので、全体計算量
が達成できます。もしmapを使えばもう1つ
が付きますが十分間に合うと思います。
※ のときは1回でも繰り上がりが起こってしまうとその時点でアウトなので、上の解析によらず最悪でも
で判定できます。また答えが1になるのは
が狭義単調増加である場合だけなので、二分探索を回す前に狭義単調増加であるかだけを調べてしまってもよいですね。
ACコード
D - Grid game
解法
「2回連続で駒が動かされなかったら終了する」ので、高橋くんは動かし続けるしかありません。逆に青木くんはなるべく早く駒を動かせない状態に持っていきたいです。高橋くんが駒を動かせない状態というのは、駒の下のマスに障害物または外壁がある状態です。青木くんはなるべく早く障害物に「上から」駒をぶつけてしまいたいです。
まず、青木くんが常に駒を動かせるような場合を考えてみます。
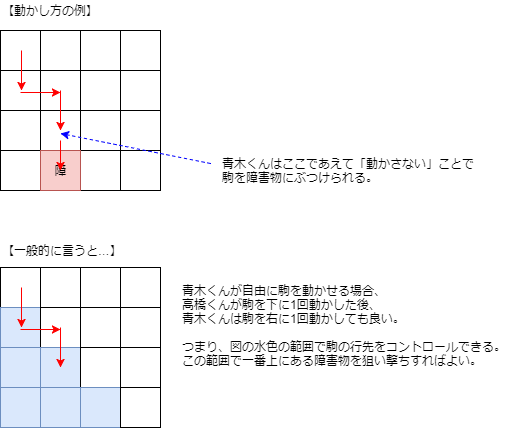
青木くんが常に駒を動かせる場合、上の図のように考えることで、下のマスに行くほど青木くんが駒を操作できる横の範囲が広がります。水色の範囲内で最も上にある障害物を探すことで答えが求められます。
ただ青木くんが常に駒を動かせるとは限りません。以下の図のような場合を考えてみましょう。

この図のように、青木くんが右に動こうとしたときに障害物にぶつかってしまうことがあります。この時は駒を操作できる範囲を広げることはできません。
このように、列(行でもいいです)を1つずつ見ていきながら、青木くんがどの範囲の障害物にぶつけられるかを考えていくことで答えを求めることができます。
ACコード
実装ですが、障害物を行または列ごとにまとめて管理し、ソートして順番に見ていくとよいでしょう。コード中の loss が、障害物のせいで青木くんが範囲を広げられなかった回数を示しています。