ABC105 参加記録
結果は25分台全完で45位。1WAを出したのが良くないですね…

A - AtCoder Crackers
せんべいをなるべく均等に配ったとき、枚数が人数で割り切れるときはぴったり同じ枚数にできますが、そうでない場合は多い人と少ない人で1枚の差ができてしまいます。余りの値で分岐します。
Submission #2983736 - AtCoder Beginner Contest 105
B - Cakes and Donuts
の形をした方程式の、整数解を求める問題。負の値を取っていいなら最大公約数を考えることになりますが、今回は非負の値に限定されているのと、制約がとても小さいので素直に全探索します。
合計金額を超えない範囲で4の倍数 を列挙して、
が7の倍数か調べればよいです。
Submission #2984464 - AtCoder Beginner Contest 105
C - Base -2 Number
これは難しいと言うか、問題を見た瞬間にちょっとヤバそうな雰囲気がありましたね…
-2進数をいきなり考えるのは難しいので、慣れ親しんだ2進数について少し振り返りましょう。2進数の 桁目(0始まりとします)は、元の数の「
成分」を表現します。

2進数において、以下のことが言えます。
- 下から2ビット目以上が担当する値は全て2の倍数なので、「2で割った余り」は、一番下のビットだけで決まる。
- 同じく、「4で割った余り」は、下2つのビットだけで決まる。
- 同じく一般に、「
で割った余り」は、下位
ビットだけで決まる。
これを利用して、10進数を2進数に変換する際に、余りを使って下位ビットから決定していくことができます。これはお馴染みですね。
def to_bin(n) return '0' if n == 0 digits = [] i = 0 base = 1 while n != 0 if n % (base*2) == 0 digits[i] = '0' else digits[i] = '1' n -= base end i += 1 base *= 2 end return digits.reverse.join end
さて-2進数です。実はこれと同じことが言えます。
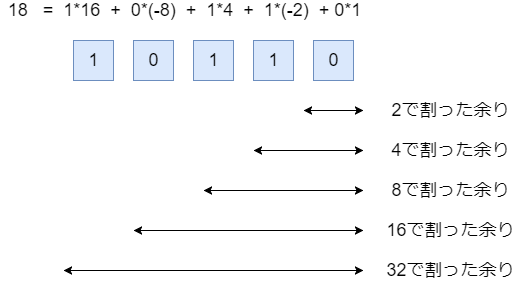
-2はやっぱり2の倍数であり、-8はやっぱり8の倍数です。そのため、「 で割った余りは、下位
ビットだけで決まる」という性質は同様です。そのため、同じように下位ビットから決める処理をすることができます。
def to_m2(n) return '0' if n == 0 digits = [] i = 0 base = 1 while n != 0 if n % (base*2) == 0 digits[i] = '0' else digits[i] = '1' n -= base end i += 1 base *= -2 # ここが違う! end return digits.reverse.join end
各桁が担当している値(コード中では base )が-2倍ずつ増えていくことを除けば、2進数の実装と同じですね。
細かい点として、剰余計算の仕様は言語によって様々なのでそこは注意です。「余りが0かどうか」だけで判断していけば、大抵の言語では恐らくそんなに困らないです。
本番コードでは base に-2を掛けていく代わりに、 n を2で割っていって、ビットが立っている時の調整処理で正負を分けています。自分自身が正負を間違えにくい方法なら何でもいいと思います。
Submission #2986709 - AtCoder Beginner Contest 105
逆に上位ビットから決定する…というのもできそうではありますが、ビットが1になる条件がころころ変わるので少し面倒だと思います。いずれにせよ、慣れ親しんだ「10進数から2進数への変換」から始めて、-2進数だとどこを変更する必要があるのか?を考えて解くのがいいと思います。
ちなみに本番WAはサンプルにも用意されている「0」です。サンプルにあるケースでWA出すのはひどい…
D - Candy Distribution
要素数 なので、全区間を調べていてはTLEです。効率的な探し方を考えましょう。
区間の要素の和を求める問題で、単調性がないような場合、累積和を考えてみるとよいです。というのは、区間 ] の要素和を、累積和
] と
] の差として考えることができるからです。
今回は、以下のように考えることができます。
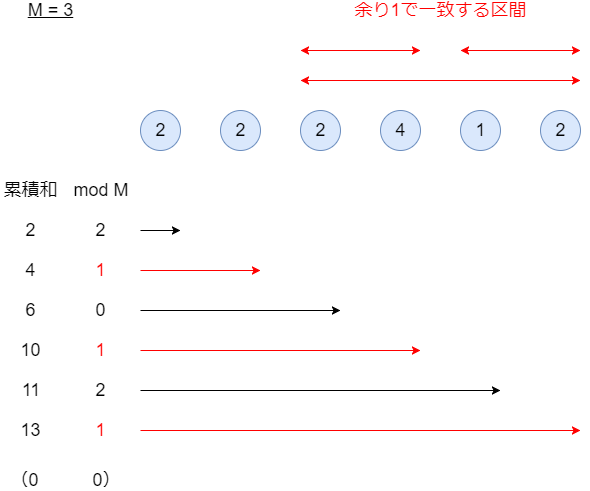
区間 ] の要素和が
で割り切れるということは、累積和
] と
] の
で割った余りが等しいということと同じです。そのため、各要素について「最初からその要素までの累積和を
で割った余り」を調べて、それが等しいような組み合わせを探せば良さそうです。
数列の頭から最初から累積和を取りながら、「累積和の余りが になっているような右端の個数」を
ごとに数えていきます。「数列の最初から取る」という場合を取りこぼさないように、最初には余り0の右端がある、というふうに考えます。
条件を満たす区間の個数は、累積和を取る操作の途中で「それより左にあって、累積和の余りが同じ右端の個数」をどんどん足していっても良いですし、最後まで集計が終わってから のような計算をしても良いでしょう。
Submission #2988059 - AtCoder Beginner Contest 105
数ヶ月前のAGCで類似問題が200点問題として出たので、印象に残っている人も多いのではないでしょうか…
さいごに
C問題が難しかったですね…