AtCoder World Tour Finals 2019 B - Multiple of Nine

解説ACしたので、自分の理解のためにも公式解説よりも少し詳しい解説を書いていきます。

区間の条件を累積和の条件に落とし込む

「非負整数を9で割った余りは10進数での桁和を9で割った余りと等しい」という性質を使います。

$i$ 番目の数字を $d_{i}$ と表記します。 $d_{1}$ から $d_{i}$ までの累積和を9で割った余りを $s_{i}$ と表記します（ただし $s_{0} = 0$ ）。以降は9で割った余りを単に累積和と呼びます。

こうすると区間 $\lbrack l, r\rbrack$ が表す整数が9の倍数であることは、そのすぐ外側にある累積和 $s_{l-1}, s_{r}$ が等しいことと同値であることが言えます。

ただし、複数のクエリが同じ累積和を共有することがあります。その場合は条件式が結合されます。

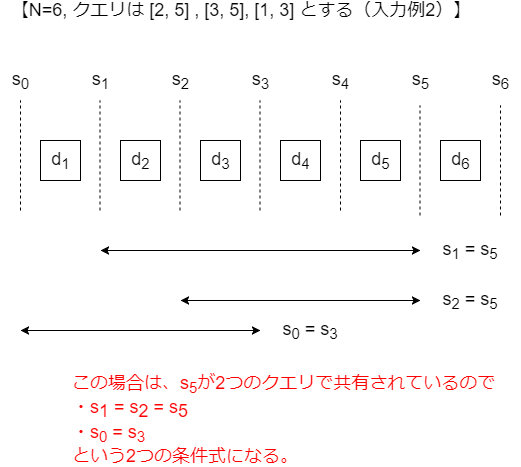
このようにクエリの集合を、「mod9で取った累積和のどこかが等しい」という条件の集合に落とし込むのが第一歩です。この結合された後の条件式の個数を $Q^{\prime}$ とします。全ての累積和が異なっていれば $Q^{\prime} = Q$ で、そうでなければ $Q^{\prime} \lt Q$ です。

以降、いずれかの条件式に登場する累積和を「大事な累積和」と呼ぶことにします。

累積和の間の場合の数を考える

全ての条件式の大事な累積和を集めてソートして、それぞれの累積和の位置で数列を分割します。ソートされたときに隣り合っている大事な累積和を「隣り合う累積和」と呼ぶことにします。

隣り合う累積和に挟まれたブロックについて、数字を選ぶ場合の数を考えます（両端のブロックは後で考えます）。1ブロックの中の数字の選び方に関係するのは、その両端にある隣り合う累積和の差です。ブロックの中の数字の合計を9で割ったものが、両端にある大事な累積和の差（mod9）と一致しなければなりません。

具体的に数えてみます。例えば1ブロックに含まれている数字の個数が3つだったとします。3つの数字の選び方は全部で1000通りです。そして3つの数字の合計を9で割った余りの分布は、0～999までの整数を9で割った余りの分布と等しいので

0：112個
1：111個
2：111個
...
8：111個

となり、0になるものが1個だけ多いです。これは文字数が3でない場合にも同様に計算できて、文字数が $n$ のとき余りが1～8になる場合の数はそれぞれ $\frac{10^{n}-1}{9}$ で、余りが0になる場合の数はそれに1足したものになります。

つまりそれぞれのブロック中の数字の選び方を求めるためには、その両端にある隣り合う累積和が等しいかどうかを考える必要があります。

大事な累積和の値の取り方についてDPする

最初に見たように、大事な累積和は「このグループに属する累積和たちは値が等しい必要がある」という $Q^{\prime}$ 個のグループに分かれています。それぞれのグループに0～8を割り当てていけば全てのパターンを列挙できますが、 $9^{Q^{\prime}}$ パターンあるので単純な全列挙はできません。

このグループには大事な累積和がごちゃ混ぜの位置で入っているため、「左から順番に決めていく」みたいな方法を取るのも難しいです。そこで「値が同じである累積和のグループを一気に決める」ことを考えます。具体的には次のようなDPです。

$dp \lbrack i \rbrack \lbrack S \rbrack$ ：累積和の値が $0, 1, ..., i$ になるようなグループまで選び終わっていて、割り当て終わったグループの集合が $S$ であるような○○

この○○は何にすれば良いでしょうか。ある $i$ について「こことここの累積和が $i$ になる」として決めた時、それらの累積和に隣り合ったものがあれば、先程見たようにその間にあるブロックについて「場合の数が1多くなる」現象が発生します。このとき、「全累積和が異なる」ことを仮定したときの場合の数は最後に掛けることにして、DPテーブルにはあるブロックの場合の数が1多くなったことによって得られる倍率（係数）を格納していくという荒業を使います。先程の例で言うと $\frac{112}{111}$ をDPの値に掛けます。

ということでDPテーブルの定義は以下のようになります。

$dp \lbrack i \rbrack \lbrack S \rbrack$ ：累積和の値が $0, 1, ..., i$ になるようなグループまで選び終わっていて、割り当て終わったグループの集合が $S$ であるときの、「全累積和が異なる」ことを仮定したときの各ブロックの場合の数の積と比較して得られる係数

そして「全累積和が異なる」ことを仮定したときの場合の数は別途計算して、DPの初期値にするか最後に掛けてあげればよいです。

このDPは部分集合を列挙する $O(3^{Q^{\prime}})$ のDPとなります。具体的に $dp \lbrack i \rbrack \lbrack S \rbrack$ を求める時は、値を $i$ にするグループの集合 $T$ を $S$ の全ての部分集合として列挙し全て合計します。 $i-1$ までに得られている係数は $dp \lbrack i-1 \rbrack \lbrack S-T \rbrack$ であり、これに集合 $T$ を同じ値にしたときに得られる係数を掛けます。

この「集合 $T$ を同じ値にしたときに得られる係数」は全ての $T$ について事前に計算しておくことが出来ます。各 $T$ について、隣り合う累積和が含まれているかをチェックし、含まれている場合はその間にある文字数を $n$ として $(\frac{10^{n}-1}{9} + 1) \div \frac{10^{n}-1}{9}$ を掛けていけば良いです。この前計算は $O(Q^{\prime}2^{Q^{\prime}}$ ) で出来ます。

両端のブロックについて考える

ここで先程後回しにしていた、どの区間にも含まれない両端のブロックについて考えます。

まず一番右のブロックは好きに選んで良いです。文字数を $n$ として $10^{n}$ の係数が掛かります。

次に一番左のブロックですが、左端の累積和は $s_{0} = 0$ です。つまり一番前のブロックの文字数を $n$ 、大事な累積和のうち一番左にあるものを $s_{f}$ として、場合の数は $s_{0} \ne s_{f}$ ならば $\frac{10^{n} - 1}{9}$ であり $s_{0} = s_{f}$ であればそれより1大きい値です。

この値を、DPの中で「 $s_{f}$ を含むグループが選ばれるタイミング」で $s_{f}$ の値に応じて掛け算してあげればよいです。

また、もう少し計算が簡単な方法として、DPの対称性を利用する方法があります。このDPでは各グループに割り当てた余りをまるっと入れ替えても同じになるので、 $s_{f}$ の値に応じた値をそれぞれ掛け算する代わりに「最初のブロックは好きに選んで良い、そのかわり $s_{f}$ の値は何か1つ（例えば0）に固定されている」という条件でDPをしてもよいです。公式解説の数式はこっちになっていると思います。

解法まとめ

上記の内容を手順としてまとめます。

まず入力のクエリを「累積和が等しい」という条件に置き換える。このとき条件式が結合するものはまとめてグループ化しておく。
グループの集合 $2^{Q^{\prime}}$ 個について、「そのグループに含まれる累積和が等しいときに、隣り合う累積和が等しいことによって得られる係数」を前計算しておく。
部分集合列挙DPを行う。
最後に全体に掛かる係数（公式解説にある数式1）を掛ける