2020-09-27

ACL Beginner Contest F - Heights and Pairs

解法

まずは入力を各身長ごとの人数として集計します。 $a_{i}$ を身長が $i$ である人の人数とします。 $\sum_{i} a_{i} = 2N$ であり、 $0$ 人であるような身長を無視すれば身長の種類数は $2N$ 以下です。

条件を満たす組み方をDPなどで直接数えようとすると、 $O(N^{2})$ から落ちず厳しいです。

包除原理を適用します。同じ身長で組んでいるペアを「違反ペア」と呼ぶことにして、違反ペアを $0$ 個以上集めた集合を $s$ とします。「 $s$ に含まれるペアは必ず組んであって、その他のペアは自由に組まれているような組み方の数」を $C(s)$ とすると、答えは包除原理から

$\displaystyle \sum_{s} (-1)^{|s|}C(s)$

と計算できます。集合 $s$ の取り方は膨大にあるので $s$ のサイズごとに集計することにします。

まずはそれぞれの身長ごとに独立に、違反ペアをいくつか組む組み方を数えます。以下の値を計算します。

$c\lbrack i\rbrack\lbrack k\rbrack =$ 身長が $i$ の人の中で、違反ペアをちょうど $k$ 組だけ組むような組み方。（それ以外の人の組み方はまだ決めない）

これはまず、違反ペアに参加する人を選ぶのが $_{a_{i}}C_{2k}$ 通り。その中で違反ペアを組む組み方は、

まず $1$ 人適当に誰かを選び、その人の相方を残りの $2k-1$ 人の中から選ぶ。
また $1$ 人適当に誰かを選び、その人の相方を残りの $2k-3$ 人の中から選ぶ。
…

と考えると、二重階乗を用いて $(2k-1)!!$ 通りと計算できます。この $k$ は $0$ から $\lfloor\frac{a_{i}}{2}\rfloor$ まで取り得ます。

各身長ごとに求めた数列 $c\lbrack i\rbrack$ を全てマージします。身長 $1$ の人の違反ペアが $b_{1}$ 組、身長 $2$ の人の違反ペアが $b_{2}$ 組…という組み方を合わせると、合計違反ペアが $b_{1} + b_{2} + \cdots$ 組であるような組み方が $c\lbrack 1\rbrack\lbrack b_{1}\rbrack\times c\lbrack 2\rbrack\lbrack b_{2}\rbrack\times\cdots$ 通り得られます。これを全ての $(b_{1}, b_{2}, ...)$ について計算するので、これは数列をFFT（NTT）でマージすることに相当します。

これを最後までマージすると、以下の値を示す数列が得られます。

$c_{all}\lbrack k\rbrack =$ 全ての人の中で、違反ペアをちょうど $k$ 組だけ組むような組み方。（それ以外の人の組み方はまだ決めない）

これに残りのペアの組み方 $(2(N-k)-1)!!$ を掛けると、「 $|s| = k$ であるような $s$ についての $C(s)$ の和」が得られます。これを包除原理の式に従い合計すると答えになります。

あとはNTTのマージにかかる計算量を落とす必要があります。各身長に対する $c\lbrack i\rbrack$ の長さは $\lfloor\frac{a_{i}}{2}\rfloor + 1$ であり、 $\sum_{i} a_{i} = 2N$ なので、全ての数列の長さの和は $2N$ 以下です。

何も考えずにマージすると、長い数列に短い数列を何回もマージするような場合に最悪で $O(N^{2}\log N)$ の計算量が掛かってしまいます。

マージの順番を工夫して、以下の二分木のようにマージをするとどうでしょうか。

f:id:betrue12:20200927042025p:plain

二分木の1段分のマージでは、長さの和が $2N$ 以下である数列たちが1度ずつNTTでマージされるので、合計で計算量 $O(N\log N)$ になります。そして二分木のようにマージすると $O(\log N)$ 段で全てマージし終わるので、全体計算量 $O(N (\log N)^{2})$ でマージできます。

数列の本数が2冪でないときはトーナメントのシードのような扱いをします。また二分木でのマージとは挙動が少し異なりますが、数列たちをキューに入れて「先頭から $2$ 本取り出してマージした結果を末尾に入れる」という処理を $1$ 本になるまで繰り返しても同様の計算量が達成できます。

ACコード

Submission #17047575 - ACL Beginner Contest
（AtCoder Library使用）Submission #17058173 - ACL Beginner Contest

2020-09-27

ACL Beginner Contest E - Replace Digits

AtCoder プログラミング競技プログラミング

E - Replace Digits

先日、AtCoder Libraryの遅延伝播セグメント木の使い方について記事を書きました。

AtCoder LibraryのLazy Segtreeの使い方 - ARMERIA

今回の問題はセグ木にちょっと変なものを乗せる問題なので、上記の記事で解説していることの実践編として書いていこうと思います。この記事を読む前に上記の記事を読むことをオススメします。

解法

区間更新クエリと全体取得クエリを処理する問題です。遅延伝播セグメント木に乗せることを考え、まずは各ノードの data として何を持てば良いかを考えます。後で足りない情報があれば足すとして、まずは一番大事な「各桁の値」をどう持つか考えましょう。

これには何通りか方法があって、例えば $S$ 全体が $23415$ だったときに、末端のノードが持つ値を $\lbrace 2, 3, 4, 1, 5\rbrace$ と持つ方法や、 $\lbrace 20000, 3000, 400, 10, 5\rbrace$ と持つ方法があります。どちらでも解けますが今回は後者で考えてみます。

末端のノードが持つ値を $\lbrace 20000, 3000, 400, 10, 5\rbrace$ のようにすれば、区間同士をマージする二項演算 op は単なる足し算で良いです。この data だけを記したセグメント木の全体構造は以下のようになります。

f:id:betrue12:20200927012610p:plain

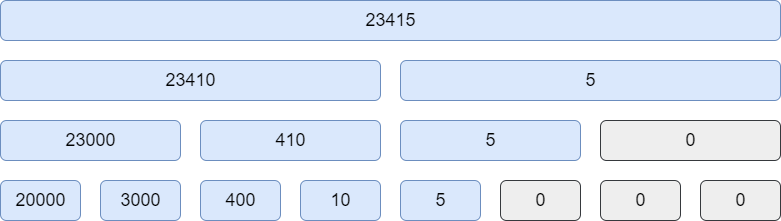
次に lazy として持つ「操作を表す値」を考えますが、これは更新クエリで書き換える1桁の整数をそのまま持てば良いでしょう。値を上書きする更新クエリなので、冒頭で紹介した記事の「区間更新操作の恒等写像」に書いたように恒等写像 id と操作同士をマージする関数 composition を定義します。

問題は操作を data に対して行う関数 mapping です。ある区間内の数字を一様に上書き更新したときに、その区間が受け持つ値が何になるべきかは区間によって異なります。例えば下図において赤色で塗っている区間 $\lbrack 0, 2)$ は万の位から千の位までの合計を担当しているので、「区間 $\lbrack 0, 2)$ の数字を一様に $d$ に変更する」という操作によってこのノードが持つデータは $11000\times d$ になるべきです。

f:id:betrue12:20200927014224p:plain

この $11000$ というのは、「そのノードが持つ区間内の数字を一様に更新したときに、その数字に対していくつの係数を掛ければその区間が受け持つ値の和になるか」という値です。これも一緒に data として持ってしまうことにしましょう。末端ノードについては右から $1, 10, 100, ...$ という値を持たせておいて、マージする関数 op においてこっちも単に足し算をしてあげれば良いです。各ノードが持つ data は以下のような構造になります。

f:id:betrue12:20200927012914p:plain

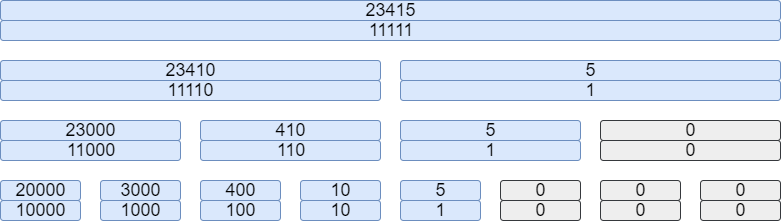
この値があれば mapping も定義できます。

最後に、全ての加算は $\bmod 998244353$ で行うので、都度余りを取るか modint を用いると良いです。

ACコード（AtCoder Library使用）

Submission #17051688 - ACL Beginner Contest

2020-09-23

AtCoder LibraryのLazy Segtreeのチートシート

AtCoder プログラミング競技プログラミング

AtCoder LibraryのLazy Segtreeの使い方 - ARMERIA

こちらの記事でAtCoder LibraryのLazy Segtreeの使い方を説明しましたが、コンテスト中に読んでられっか！みたいな時のためにコピペで使えるチートシートをまとめます。整数列に対する、以下の組み合わせ6種類です。

区間変更クエリ：加算、更新
区間取得クエリ：最小値、最大値、和

オーバーフローで死なないように整数列の要素を long long で扱っています。また INF および ID として $8\times 10^{18}$ を使います。

区間加算・区間最小値取得
区間加算・区間最大値取得
区間加算・区間和取得
区間変更・区間最小値取得
区間変更・区間最大値取得
区間変更・区間和取得

区間加算・区間最小値取得

AOJ（RMQ and RAQ）提出：Aizu Online Judge

using S = long long;
using F = long long;

const S INF = 8e18;

S op(S a, S b){ return std::min(a, b); }
S e(){ return INF; }
S mapping(F f, S x){ return f+x; }
F composition(F f, F g){ return f+g; }
F id(){ return 0; }

int main(){
    int N;
    std::vector<S> v(N);
    atcoder::lazy_segtree<S, op, e, F, mapping, composition, id> seg(v);
}

区間加算・区間最大値取得

using S = long long;
using F = long long;

const S INF = 8e18;

S op(S a, S b){ return std::max(a, b); }
S e(){ return -INF; }
S mapping(F f, S x){ return f+x; }
F composition(F f, F g){ return f+g; }
F id(){ return 0; }

int main(){
    int N;
    std::vector<S> v(N);
    atcoder::lazy_segtree<S, op, e, F, mapping, composition, id> seg(v);
}

区間加算・区間和取得

区間幅が必要なので値を構造体で持ちます。seg.prod(l, r).value で値を取り出してください。

AOJ（RSQ and RAQ）提出：Aizu Online Judge

struct S{
    long long value;
    int size;
};
using F = long long;

S op(S a, S b){ return {a.value+b.value, a.size+b.size}; }
S e(){ return {0, 0}; }
S mapping(F f, S x){ return {x.value + f*x.size, x.size}; }
F composition(F f, F g){ return f+g; }
F id(){ return 0; }

int main(){
    int N;
    std::vector<S> v(N, {0, 1});
    atcoder::lazy_segtree<S, op, e, F, mapping, composition, id> seg(v);
}

区間変更・区間最小値取得

AOJ（RMQ and RUQ）提出：Aizu Online Judge

using S = long long;
using F = long long;

const S INF = 8e18;
const F ID = 8e18;

S op(S a, S b){ return std::min(a, b); }
S e(){ return INF; }
S mapping(F f, S x){ return (f == ID ? x : f); }
F composition(F f, F g){ return (f == ID ? g : f); }
F id(){ return ID; }

int main(){
    int N;
    std::vector<S> v(N);
    atcoder::lazy_segtree<S, op, e, F, mapping, composition, id> seg(v);
}

区間変更・区間最大値取得

using S = long long;
using F = long long;

const S INF = 8e18;
const F ID = 8e18;

S op(S a, S b){ return std::max(a, b); }
S e(){ return -INF; }
S mapping(F f, S x){ return (f == ID ? x : f); }
F composition(F f, F g){ return (f == ID ? g : f); }
F id(){ return ID; }

int main(){
    int N;
    std::vector<S> v(N);
    atcoder::lazy_segtree<S, op, e, F, mapping, composition, id> seg(v);
}

区間変更・区間和取得

区間幅が必要なので値を構造体で持ちます。seg.prod(l, r).value で値を取り出してください。

AOJ（RSQ and RUQ）提出：Aizu Online Judge

struct S{
    long long value;
    int size;
};
using F = long long;

const F ID = 8e18;

S op(S a, S b){ return {a.value+b.value, a.size+b.size}; }
S e(){ return {0, 0}; }
S mapping(F f, S x){
    if(f != ID) x.value = f*x.size;
    return x;
}
F composition(F f, F g){ return (f == ID ? g : f); }
F id(){ return ID; }

int main(){
    int N;
    std::vector<S> v(N, {0, 1});
    atcoder::lazy_segtree<S, op, e, F, mapping, composition, id> seg(v);
}

2020-09-22

AtCoder LibraryのLazy Segtreeの使い方

AtCoder プログラミング競技プログラミング

AtCoder Libraryが遅延伝播機能を持つセグメント木 atcoder::lazy_segtree を提供しているものの、何か渡すものいっぱいあるしドキュメントは数学用語だらけだしよく分からん！みたいな人向けの記事です。

問題を解いていて、セグメント木に必要な機能（区間加算操作と区間最小値取得がしたい！みたいな）が明確になったときに、それを実現するためには atcoder::lazy_segtree の生成時に何を渡せばいいかを考えられるようになることがこの記事の目標です。ただしコンテスト中に読める分量ではなくなったので、整数列に対する単純な機能の組み合わせについてはコピペで使えるチートシート的なものを別途作る予定です。→作りました

対象読者は「セグメント木（抽象化も遅延伝播もナシで可）を書いたことがあって、その構造と動作の仕組みについて何となく理解している人」くらいを想定しています。もちろん遅延伝播の仕組みと内部実装を知っておくに越したことはないので、以下の記事を読んでおくことをオススメします。私もこの記事で勉強しました。

遅延評価セグメント木をソラで書きたいあなたに - hogecoder

また、この記事を書こうと思ったきっかけはお題箱の「AOJのRSQ and RUQをAtcoder Libraryでどう解けばいいか」というリクエストでした。その答えは最後のほうに書いています。

AtCoder Libraryの公式ドキュメント

https://atcoder.github.io/ac-library/document_ja/lazysegtree.html

遅延伝播セグメント木の機能

遅延伝播セグメント木を使うと、整数列などのデータ列 $a_{0}, ..., a_{n-1}$ に対して以下の2つのクエリを処理できるようになります。

区間変更クエリ：指定した区間内のデータ $a_{l}, ..., a_{r-1}$ それぞれに対して、一様に何らかの変更操作を行います。
区間取得クエリ：指定した区間内のデータ $a_{l}, ..., a_{r-1}$ に対して何らかの計算を行った結果を得ることができます。

例えばこういう問題が解けるようになります。

変更クエリ・取得クエリでそれぞれどういう処理を行うかは解きたい問題によって変わります。atcoder::lazy_segtree は生成時にこれらの処理内容をプログラマーが与えることで、1つのライブラリで様々なクエリの組み合わせを実現できるようになっています。これは非常に便利で強力である反面、使い方が難しくなりがちです。この記事ではその使い方を学びます。

またやりたい処理が何でもかんでもセグメント木で扱えるわけではなく、特定の性質を満たしている必要があります。そのことについても終わりの方で説明します。

遅延伝播の仕組み

遅延伝播セグメント木はこんな形をしています。

f:id:betrue12:20200922142356p:plain:h300

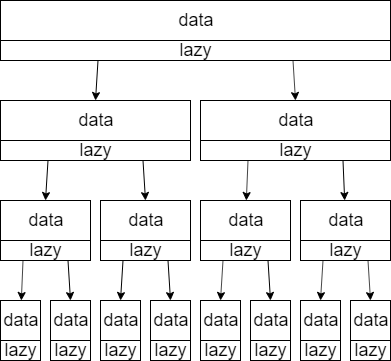
区間を担当する各ノードが data と lazy の2つの値を保持しています。 atcoder::lazy_segtree の内部実装ではそれぞれ d と lz です。

data：一番下のノードは列の各要素を保持する。その上にあるノードは、受け持つ区間の要素に対して取得演算を行った結果（区間最小値取得の機能を持つセグ木なら、その区間の最小値）を保持する。
lazy：その区間に対して行われた操作のうち、まだ自身より下のノードに作用させていないものを保持する。

data は通常のセグメント木と同じです。lazy が遅延伝播のキモで、操作をすぐに全ノードに伝播させず、必要になるまで上側にあるノードが溜めます。逆に言えば各ノードが持っている data は、自身の上にあるノードたちが lazy として溜めている操作が全て降りて来るまでは正確な（最新の）値とは限らない、ということです。

※そのため、もう伝える先がない末端のノードの lazy は実際には不要です。AtCoder Libraryの内部実装でもここの領域は確保されていません。

ある広い区間に対して何度も操作クエリが行われた時、それを末端のノードまで毎回伝えていくと計算量が増えてしまいます。なのでノード全体を覆うような操作はそのノードがずっと溜めておいて、その中のより狭い区間に対するクエリが来たときに初めて下に伝えていく。これが遅延伝播の仕組みです。

f:id:betrue12:20200922195813p:plain

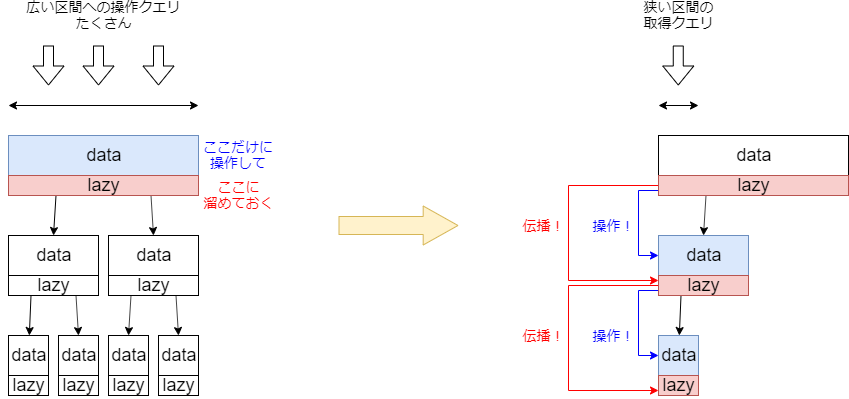
とりあえずここまで理解できればOKです。atcoder::lazy_segtree に渡す型や関数の説明ができるようになります。

テンプレート引数の作り方

atcoder::lazy_segtree のコンストラクタは以下のように定義されています。

(1) lazy_segtree<S, op, e, F, mapping, composition, id> seg(int n);
(2) lazy_segtree<S, op, e, F, mapping, composition, id> seg(vector<T> v);

具体例として「整数の数列に対する、区間加算操作と区間最小値取得」の機能を持つセグメント木を作るために、<> の中のテンプレート引数として何を渡すべきか考えてみましょう。この例にしたのはイレギュラーなパターンが一番少ないからです。

`S` と `F`

S は data、つまり各要素および区間取得結果の型です。整数の数列なら int や long long などです。

F は lazy、つまり操作（写像）を表す値の型です。整数を加算する操作なら同じく int や long long などです。

今回の場合は両方 int とします。int と直接書いても良いですし、using S = int; などと別名を付けて S と書いても良いです。

`S op(S a, S b)`

区間取得をどのような演算で行うかを定義します。通常のセグメント木と同じです。

ドキュメントの使用例にあるように、関数を別途定義してその関数名を引数に書けば良いです。区間最小値取得なら S op(S a, S b){ return std::min(a, b); } を作って op を渡します。ドキュメントの関数名と合わせる必要はありません。

`S mapping(F f, S x)`

操作 f を各ノードが持つ data の値 x に対して作用させる関数です。この mapping と次の composition が、先ほど伝播の仕組みを説明した図においてどこに該当するかを示します。

f:id:betrue12:20200922195827p:plain

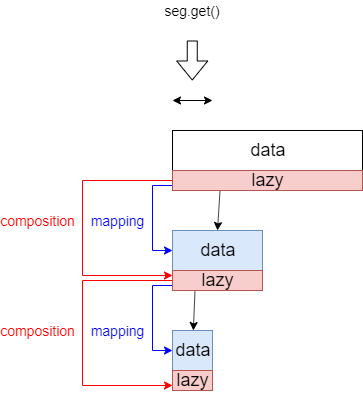
区間加算操作・区間最小値取得の場合を考えます。末端のノードの data は数列の各要素1つに該当するので、加算操作では単に f を x に足せば良いです。ですがここでは「上側のノードが持つ値、つまり既に取得演算をしてしまった値に対して操作しても大丈夫か？」という点に注意する必要があります。

例えば区間 $\lbrack 0, 4)$ を受け持つノードは data として $\min(a_{0}, a_{1}, a_{2}, a_{3})$ の値を保持しています。この区間に対して「区間内の全要素に整数 $f$ を加算する」という操作を行うと、この data の値は $\min(a_{0}+f, a_{1}+f, a_{2}+f, a_{3}+f) = \min(a_{0}, a_{1}, a_{2}, a_{3}) + f$ となります。

同様にどのノードであっても、操作 f を行った時には元々持っていた data の値に f を足せば良いです。そのため mapping の定義は S mapping(F f, S x){ return x+f; } となります。

区間和取得の機能を持たせる場合は少し面倒です。後で説明します。

`F composition(F f, F g)`

既にこれまでの操作を溜めている lazy に対して、さらに新しい操作を追加する関数です。g がこれまでの操作、f が後に追加する操作で、「その2つの操作を順に行うようなひとまとめの操作（合成写像）」を返します。

区間加算操作の場合、「g を足す」という操作の後に追加で「f を足す」という操作は、合わせると結局「f+g を足す」という操作になります。なので composition の定義は F composition(F f, F g){ return f+g; } とします。

今回の場合は足し算が可換な演算なので気にしなくても良いですが、可換でない場合には順番に注意しましょう。f のほうが後の操作です。

`S e()` と `F id()`

それぞれ、区間取得演算 op の単位元と区間操作演算 mapping における恒等写像を返す関数です。関数として渡す仕様になっていますが、この値がプログラムの途中で変わることはほぼないので定数を返す関数を作れば良いです。

二項演算 op の単位元 e とは、全ての a に対して op(a, e) = op(e, a) = a を満たすものを指します。区間最小値取得の場合は「（自身相手でない限り）絶対に最小値として採用されないような値」、つまり $\infty$ とすれば良いです。実装上は data が取り得ないような十分大きな整数を使います。例えば data が最大で $10^{9}$ までの値を取り得る場合、S e(){ return int(1e9)+1; } とすれば良いです。

操作を行う関数 mapping における恒等写像 id とは、全ての a に対してmapping(id, a) = a となるものを指します。区間加算操作の場合は「足しても絶対に対象の値を変えないような値」、つまり $0$ を使います。F id(){ return 0; } とすれば良いです。

よく使う単位元や恒等写像として、最小値であれば $+\infty$ 、最大値であれば $-\infty$ 、和や加算であれば $0$ 、積や乗算であれば $1$ を使えば良いです。更新操作の場合は？恒等写像がないですね。後で説明します。

完成！

これで全部の型と関数が定義できました。以下のように使うことができます。

using S = int;
using F = int;
S op(S a, S b){ return std::min(a, b); }
S e(){ return int(1e9)+1; }
S mapping(F f, S x){ return x+f; }
F composition(F f, F g){ return f+g; }
F id(){ return 0; }

int main(){
    std::vector<int> v = {0, 1, 2, 3, 4};
    atcoder::lazy_segtree<S, op, e, F, mapping, composition, id> seg(v);
}

変数名として使いたい S とか e がグローバルに置いてあると何かと面倒だと思うので、適宜名前は変えて良いです。

注意すべきケース

いくつか注意すべきケースを説明します。

区間和を取る場合の `mapping`

区間加算操作・区間和取得の機能を持たせる場合の mapping の実装を考えます。

区間 $\lbrack 0, 4)$ を受け持つノードの data の値は $a_{0} + a_{1} + a_{2} + a_{3}$ です。ここに「区間内の全要素に $f$ を加算する」という操作を行うと、その値は $a_{0} + a_{1} + a_{2} + a_{3} + 4f$ となるべきです。つまり元々持っていた値に $f \times (区間の幅)$ を足す必要がありますが、mapping の引数では区間の幅が渡されていません。

この場合は公式ドキュメントの使用例に倣い、data のほうに区間の幅を持ちます。例えば data の型 S を

struct S{
    int value;   // 実際の値
    int size;    // 区間の幅
};

という構造体で定義します。末端の要素については data[k].size = 1 として、区間取得の演算を S op(S a, S b){ return {a.value + b.value, a.size + b.size}; } とすれば、各ノードが持つ区間幅が適切に求められます。

これで区間幅が使えるので、区間加算操作は S mapping(F f, S x){ return {x.value+x.size*f, x.size}; } と実現することができます。

注意点として、必ず全要素の size を $1$ にセットした vector を渡して初期化してください。単位元の size は $0$ とするので、要素数を渡して初期化してしまうと全ての data の値が単位元になり、区間幅が全て $0$ になってしまいます。

以上の内容を踏まえた、区間加算操作・区間和取得の機能を持つセグメント木の定義の全体像を示します。

struct S{
    int value;
    int size;
};
using F = int;
S op(S a, S b){ return {a.value+b.value, a.size+b.size}; }
S e(){ return {0, 0}; }
S mapping(F f, S x){ return {x.value+x.size*f, x.size}; }
F composition(F f, F g){ return f+g; }
F id(){ return 0; }

int main(){
    int n = 5;
    std::vector<S> v(n, {0, 1});
    atcoder::lazy_segtree<S, op, e, F, mapping, composition, id> seg(v);
}

応用的な使い方として、例えば座標圧縮をしたことで各末端ノードが受け持っている実際の長さが $1$ とは限らない時も、この size に入れておくと各ノードが受け持つ実際の長さが分かります。操作対象の数列の要素数がクエリ数に対して非常に多い場合に有効です。

区間更新操作の恒等写像

「区間中の値を全てある値 $x$ に更新する」という区間更新操作と、区間和取得の機能を持たせる場合を考えます。この場合恒等写像を表現できる値がないので困ります。

何通りか解決方法があって、「lazy の値として取り得ないような値を擬似的に恒等写像として扱う」方法と、「更新すべき値が存在する（恒等写像でない）かどうかのフラグをbool値で持つ」方法があります。今回は型を変えなくて良い前者を紹介しますが、「その値が lazy として本当に取り得ないか？」という点には十分注意してください。

擬似的に恒等写像として扱う値を ID とします。このとき写像を扱う関数である mapping と composition はそれぞれ以下のようになります。

S mapping(F f, S x)：f が ID ならばそのまま x を返す。そうでなければ区間内の値全てを f に変更するので、x.value = x.size * f とする。
F composition(F f, F g)：f が ID ならばそのまま g を返す。そうでなければ、後からの操作で上書きされるので f を返す。

区間和取得を考える場合、先ほどと同様に区間幅が必要な点に注意してください。

以上の内容を踏まえた、区間更新操作・区間和取得の機能を持つセグメント木の定義の全体像を示します。

struct S{
    int value;
    int size;
};
using F = int;
const F ID = int(2e9);
S op(S a, S b){ return {a.value+b.value, a.size+b.size}; }
S e(){ return {0, 0}; }
S mapping(F f, S x){
    if(f != ID) x.value = x.size * f;
    return x;
}
F composition(F f, F g){ return (f == ID ? g : f); }
F id(){ return ID; }

int main(){
    int n = 5;
    std::vector<S> v(n, {0, 1});
    atcoder::lazy_segtree<S, op, e, F, mapping, composition, id> seg(v);
}

これを用いてAOJの「RSQ and RUQ」を解いたコードが以下です。

Aizu Online Judge

bool値でフラグを持つ場合は、F の型を S と同じように構造体にしたり pair<int, bool> にしたりします。実装はだいたい同じで、最初にフラグを見て恒等写像であれば更新せずに返すという処理をします。

「セグ木に乗る」とは

やりたい演算がセグメント木に乗るとか乗らないとかいう話は、結局のところこれらの関数 op mapping composition を適切に定義できるかどうか？という点に尽きます。単位元と恒等写像はどうにでもなるので。

op は通常のセグメント木にも存在する取得クエリの演算で、これが結合法則を満たすことがまず必要です。この説明はこちらの記事に詳しく書いています。

遅延伝播を行う時にはそれに加えて、以下の2つの性質を満たすような関数を見つける必要があります。

mapping：操作を、全てのノードが持つ data に同じ計算式で作用させることができること。このとき区間幅など必要な情報を data 側に持たせて補うのはOK。
composition：複数の操作を連続して行うという操作（合成写像）を、あたかも1回の操作であるかのように扱って lazy に持たせることができること。

最後に

かなりの分量になりました。セグメント木として実現したい機能をどういう風に分解して関数を作っていけば良いか、理解する助けになれば幸いです。

Practice Contestの問題では2問とも変なものを乗せていますが、まずは整数列に対する単純な演算を実現できるよう色々練習していくのが良いと思います。AOJの区間クエリ問題集などが良いでしょうか。徐々に慣れていって、いずれは変なものを乗せられるようになりましょう。

2020-09-21

Educational Codeforces Round 11 E. Different Subsets For All Tuples

Codeforces プログラミング競技プログラミング

お題箱より。

Problem - E - Codeforces

公式解説より楽な解法があるのでそっちを紹介します。記事最後に、リクエストにあった公式解説の補足についても説明します。

問題概要

整数列 $a$ に対して、 $f(a)$ を「 $a$ の部分列（連続でなくても良い）として登場する長さ $0$ 以上の相異なる数列の個数」と定義する。

各要素が $1, ..., m$ のいずれかであるような長さ $n$ の数列は $m^{n}$ 個ある。その全てについて $f(a)$ の値を合計した値を $\bmod 10^{9}+7$ で求めよ。

制約

$1 \le n, m \le 10^{6}$

解法

※解説中の「数列」という言葉は、特に断らない限り各要素が $1, ..., m$ のいずれかであるようなものを指すことにします。

数え方についての考察

$f(a)$ の計算ルールとして、相異なる部分列の個数を数えるので、例えば $\lbrack 1, 2, 1, 3, 1, 2, 3\rbrack \to \lbrack 1, 2, 3\rbrack$ のように複数の取り出し方で同じ部分列ができる場合にも $1$ 通りとして数える必要があります。このときによく使うのが、「その部分列を取り出す位置の組み合わせのうち、最も左側から取り出すようなものだけを数える対象とする」、という考え方です。先ほどの例の場合は（先頭を $0$ 番目として） $0, 1, 3$ 番目が最も左側から取り出す位置になります。

これを踏まえて、ある長さ $k$ の数列 $s$ があった時に、それを部分列として含む長さ $n$ の数列 $a$ を数える方法を考えます。まず、先ほど考えた「最も左側から取り出す」取り出し方で $s$ の各要素に対応する $a$ の位置を決めたとします。そうすると $a$ の各要素の値の候補数は、

$s$ の要素に対応している： $1$ 通り
$s$ の要素に対応していない＆それ以降に $s$ に対応する要素がまだ存在する： $m-1$ 通り
$s$ の要素に対応している＆それ以降に $s$ に対応する要素がもう存在しない： $m$ 通り

となります。 $2$ 番目が $m-1$ 通りとなる理由は、もし $s$ における次の要素と同じ値を採用してしまった場合、そこから取り出したほうがより左側になってしまうので、「最初に決めた位置が最も左側から取り出す位置である」という決め事に反するからです。

この $a$ が何通りあるかは、 $s$ の要素に対応する最後の位置が何番目であるかによって変わってきます。公式解説ではこの「 $s$ の長さはいくつか」「 $s$ の要素に対応する最後の要素は $a$ の何番目か」を組み合わせた2重和を考えていますが、別の方法があります。DPをしましょう。

DPをする

取り出し元の数列 $a$ と部分列として取り出す数列 $s$ の組 $(a, s)$ をDPで数えます。 $a$ の要素数を $1$ つずつ増やしていきながら、 $s$ の要素数を増やすパターン、増やさないパターンのそれぞれの遷移をします。

先ほど見たように、 $s$ の要素に対応していない $a$ の要素の候補数は、まだ $s$ に対応する要素が残っているかどうかで変化します。なのでこれを考慮し、次のような状態定義をします。

$dp\lbrack i\rbrack\lbrack 0\rbrack =$ 長さ $i$ の数列 $a$ と、その部分列である長さ $0$ 以上の数列 $s$ の組であって、今後 $s$ の要素を増やす予定のもの
$dp\lbrack i\rbrack\lbrack 1\rbrack =$ 長さ $i$ の数列 $a$ と、その部分列である長さ $0$ 以上の数列 $s$ の組であって、もう $s$ の要素を増やさないもの

その時点での $s$ の長さは持たなくても良い、という点が1つの注目ポイントです。

$dp\lbrack i\rbrack$ からの遷移は以下のように列挙できます。

$dp\lbrack i\rbrack\lbrack 0\rbrack$ から、 $a$ の要素を末尾に $1$ つ増やし、 $s$ の要素としては採用しない： $m-1$ を掛けて $dp\lbrack i+1\rbrack\lbrack 0\rbrack$ に遷移
$dp\lbrack i\rbrack\lbrack 0\rbrack$ から、 $a$ の要素を末尾に $1$ つ増やし、それを $s$ の要素としても末尾に追加する： $m$ を掛けて、 $dp\lbrack i+1\rbrack\lbrack 0\rbrack$ （まだ終わらない）と $dp\lbrack i+1\rbrack\lbrack 1\rbrack$ （これで終わり）の両方に遷移
$dp\lbrack i\rbrack\lbrack 1\rbrack$ から、 $a$ の要素を末尾に $1$ つ増やし、 $s$ の要素としては採用しない： $m$ を掛けて $dp\lbrack i+1\rbrack\lbrack 1\rbrack$ に遷移

初期条件は $dp\lbrack 0\rbrack\lbrack 0\rbrack = dp\lbrack 0\rbrack\lbrack 1\rbrack = 0$ とすれば良いです。後者は $s$ として何もない状態からもう要素を増やさない、つまり空数列に対応します。答えは $dp\lbrack n\rbrack\lbrack 1\rbrack$ になります。

これなら $O(n)$ で解くことができます。

ACコード

Submission #93359107 - Codeforces

おまけ：公式解説の式変形について

元々のリクエスト内容である公式解説の式変形についても触れておきます。まず、最初に立式された

$\displaystyle \sum_{k=1}^{n}\sum_{j=0}^{n-k}\cdots$

という2重和は、 $k, j$ を2軸とする2次元平面において以下のような三角形の領域について値を全て合計しています。

f:id:betrue12:20200921043132p:plain

この領域を、 $s=j+k$ と置いた $s$ が一定の領域、つまり斜めに切って和を取るように変形しています。その上で元々の $k$ を $1$ ずらすと、次の式である

$\displaystyle \sum_{s=1}^{n}\cdots\sum_{k=0}^{s-1}\cdots$

という形になります。式の中身も「 $s=j+k$ である」「 $k$ は元々の $k$ から $1$ ずれている」と思うと変形を追いやすくなると思います。

あとは最後の二項係数の計算

$\displaystyle \sum_{k=0}^{n} {}_{r+k}C_{k} = {}_{r+n+1}C_{n}$

ですが、これはグリッド上の経路数の問題として理解することができます。 $(r+1) \times n$ マスのグリッドで左下から右上に行く経路を直接計算したものが右辺、図のように分解して足し合わせたものが左辺です。

f:id:betrue12:20200921043116p:plain

2020-09-17

キーエンスプログラミングコンテスト 2020 D - Swap and Flip

AtCoder プログラミング競技プログラミング

お題箱より。

D - Swap and Flip

解法

この問題のように「操作する場所を選んで、決められたルールに従って操作する」ということを繰り返す問題では、1回目の操作の選択、2回目の操作の選択…といった分岐パターンを直接探索していくのは非常に大変です。操作の途中過程を考えなくて良いような戦略をいかに立てるかが重要です。例えば、

操作の過程に関わらず、常に成り立っている性質や不変な量が存在する。
最終状態だけが分かれば、操作の過程を考えなくても、操作について求めたい値（最小の操作回数や操作コストの合計値、その最終状態が実現できるかどうかのYes/No判定など）が分かる方法が存在する。

というような嬉しい性質がないかを考察してみましょう。

考察1

「隣り合う2枚のカードを選び、位置を入れ替え、それぞれ裏返す」という操作の特徴を考察します。どのカードも位置が1つ移動するごとに表裏が入れ替わるので、元々あった位置と最終的な位置の差（移動距離）が偶数ならば表向き、奇数ならば裏向きになります。これはつまり、どのような操作過程を辿ったとしても、最後の各カードの位置を決めれば全てのカードの向きが一意に決まることを意味します。

考察2

最後の各カードの位置を決めたとします。初期状態からその位置に並べ替えるための操作回数の最小値は、各カードの番号（＝初期位置の並び順）を最後の位置に並べてできる順列の転倒数という値になります。すなわち「2つのカード番号 $(i, j)$ の組であって、 $i \lt j$ かつカード $i$ よりもカード $j$ のほうが左にあるものの個数」です。

転倒数の求め方として、左から順番に要素を見ていきながら「自身より左側に登場済みで、かつ自身より小さい要素」の個数を合計していくという方法があります。図のように今見ている要素を $i$ 、左側に登場済みで $i$ より大きい要素を $j$ とすると、組 $(i, j)$ は先ほどの条件を満たします。これを合計していくことで転倒数を求めることができるため、各ステップでは既に登場した要素の集合だけを覚えておけば転倒数の増加分を計算することができます。

f:id:betrue12:20200917185311p:plain

DPを組む

ここまでの考察を使って答えを求める方法を考えます。考察1、2で確認したように操作の途中経過については考える必要がないので、最終状態の並び順をいきなり考えてしまって良いです。

$N$ が小さいことから、「今までどのカードを置いたか」の集合を持ちながら1つずつ順に置くカードを決めていく、いわゆるbit DPを考えることができます。左から順番に置くカードを決めていくとすると、必要な情報は

今までどのカードを置いたか？
最後に置かれたカードはどれか？
そこまでの転倒数はいくつか？

の3点です。以下のようにDPの状態を定義します。

$dp\lbrack s \rbrack\lbrack x\rbrack =$ 既に置いたカードの集合が $s$ であって、最後に置かれたカードが $x$ で、既に置いたカードの表向きになっている値は広義単調増加になっているときの、そこまでの転倒数の最小値

$dp\lbrack s \rbrack\lbrack x\rbrack$ からの遷移として、次に置くカードの候補 $y$ を全て試します。このとき調べる必要があるのは

単調増加性は守られるか？（＝その遷移をしてもよいか？）
転倒数はいくつ増加するか？

の2点です。単調増加性については考察1より、最後に置かれたカード $x$ と次に置くカード $y$ の向きが移動距離の偶奇から決まるので実際に値を比較して判定できます。転倒数の増加分については考察2より、既に置かれたカードの集合 $s$ の中で $y$ よりも番号の大きいものを数えれば良いです。遷移先は $dp\lbrack s\cup \lbrace y\rbrace \rbrack\lbrack y\rbrack$ で、bit DPの代表例として紹介される巡回セールスマン問題に似た実装をすることになります。

このDPを計算し終わったら、カード全体の集合を $U=\lbrace 1, 2, ..., N\rbrace$ として、 $\min_{x} dp\lbrack U \rbrack\lbrack x\rbrack$ が答えです。

ACコード

Submission #9569271 - Keyence Programming Contest 2020

時間計算量は $O(N^{2}2^{N})$ です。転倒数の増加分を計算する時に毎回全要素を見ていると $O(N^{3}2^{N})$ になるので少し工夫しましょう。予め全ての $(s, y)$ に対して「集合 $s$ の中で $y$ よりも番号の大きいものの個数」を前計算しても良いですし、上記リンク先のコードでは次に置くカード $y$ を小さい番号から順に見ていきながら、増加分の変化を管理しています。

2020-09-15

AtCoder Beginner Contest 178 F - Contrast

AtCoder プログラミング競技プログラミング

F - Contrast

解法が色々ある問題。シンプルで実装も楽な解法1と、私が本番で解いた解法2を証明付きで紹介します。前者のほうが断然オススメ。

解法1

まず $A, B$ 合計で $N$ 個を超える値が存在する場合、どのように並べても $A_{i} = B_{i}$ となる箇所が存在してしまいます。この場合は No を出力して終了します。以降は、どの値の登場数も $A, B$ 合計で $N$ 個以下であるとします。

突然ですが $B$ を反転させて降順ソート状態にします。この状態で $A$ と $B$ を並べてみると、 $A_{i} = B_{i}$ となっている値は高々1種類だけであることが言えます。もし2種類以上の異なる値がそれぞれ同じ位置にある場合、それらは $A$ と $B$ において同じ位置関係で並んでいるということになり、「片方は昇順、片方は降順」という前提に反するからです。

$A_{i} = B_{i}$ となっている値が存在しない場合はこの $B$ が答えです。もし $A_{i} = B_{i}$ となっている値が存在する場合、その値を $x$ として、 $A_{i}$ も $B_{i}$ も $x$ でないような両端の領域を探します。この領域内の $B_{i}$ と、 $x$ が被っているところの $B_{i}$ を1つずつ組にしてスワップしていけば完成です。スワップする両者の位置はどちらも「 $A_{i}, B_{i}$ のうち片方は $x$ で、もう片方は $x$ でない」という状態になるのでこれで条件を満たします。

f:id:betrue12:20200914232651p:plain

この両端の領域の要素数が、 $x$ が被っている領域の要素数以上であることを示します。上の図のように長さ $a, b, c, d, e$ を定めると、

図より、 $a+b+c+d+e = N$
$x$ の登場数が合計で $N$ 個以下であることから、 $b+2c+d \le N$

であるので、不等式を変形することで $a+e \ge c$ を示すことができます。以上でこの構築の正当性が証明されました。

ACコード1

Submission #16762957 - AtCoder Beginner Contest 178

解法2

$A, B$ 合計で $N$ 個を超える値が存在する場合は No である、という点は同じです。

$A$ も $B$ も並び替えができる、と想定して解きます。最後に出力する時に、 $A$ の各要素が元々並んでいた位置に合わせて対応する $B$ の要素を並べれば良いです。

各値について $A, B$ それぞれの出現数を調べます。そして以下の図に示すように、 $B$ のほうが多い値を左側に、 $A$ のほうが多い値を右側に、同じ順序で $A, B$ ともに並べ替えます。そして各値について「 $A$ と $B$ についてその値が被っている長さ」を調べ、その長さだけ $B$ を右に巡回シフトすれば完成です。

f:id:betrue12:20200914225731p:plain

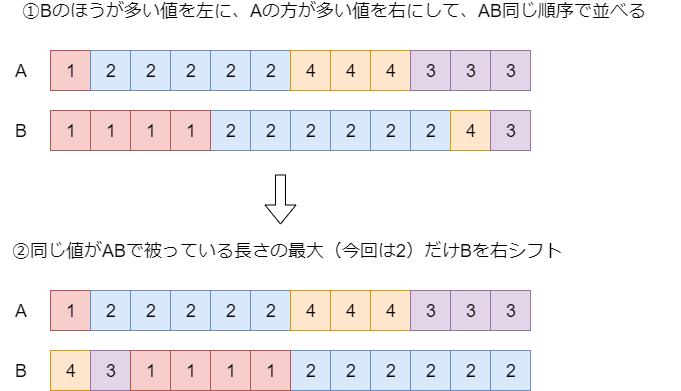
この解法の正当性を証明します。左にある値から順に見ていくと、 $B$ の方が多い値を全部先に使っているので、各値を入れる前後では常に $B$ の要素数のほうが多く（または等しく）なっています。より具体的には、全ての値について

（その値が $A$ に登場する左端） $\le$ （その値が $B$ に登場する左端）
（その値が $A$ に登場する右端） $\le$ （その値が $B$ に登場する右端）

が成立しています。図の①のほうの状況です。

この状態で被っている長さが最大であるような値を $x$ とします（図では青く塗っている $x=2$ が $2$ つ被っています）。その長さだけ $B$ を右シフトすると、全ての値について元々被っていた領域は切断されて被らなくなります。また1周して $B$ 側の右端と $A$ 側の左端がくっつくこともありません。 $x$ 以外の値が1周してくっつくためには $x$ が被っていた領域を超える必要があり、これは無理です。また $x$ についても、その登場数が合計 $N$ 個以下であることからあり得ません。

以上でこの構築の正当性が証明されました。

ACコード2

Submission #16762983 - AtCoder Beginner Contest 178

解法

ACコード

解法

ACコード（AtCoder Library使用）

区間加算・区間最小値取得

区間加算・区間最大値取得

区間加算・区間和取得

区間変更・区間最小値取得

区間変更・区間最大値取得

区間変更・区間和取得

AtCoder Libraryの公式ドキュメント

遅延伝播セグメント木の機能

遅延伝播の仕組み

テンプレート引数の作り方

S と F

S op(S a, S b)

S mapping(F f, S x)

F composition(F f, F g)

S e() と F id()

完成！

注意すべきケース

区間和を取る場合の mapping

区間更新操作の恒等写像

「セグ木に乗る」とは

最後に

問題概要

制約

解法

数え方についての考察

DPをする

ACコード

おまけ：公式解説の式変形について

解法

考察1

考察2

DPを組む

ACコード

解法1

ACコード1

解法2

ACコード2

`S` と `F`

`S op(S a, S b)`

`S mapping(F f, S x)`

`F composition(F f, F g)`

`S e()` と `F id()`

区間和を取る場合の `mapping`