AtCoder LibraryのLazy Segtreeの使い方

AtCoder Libraryが遅延伝播機能を持つセグメント木 atcoder::lazy_segtree を提供しているものの、何か渡すものいっぱいあるしドキュメントは数学用語だらけだしよく分からん！みたいな人向けの記事です。

問題を解いていて、セグメント木に必要な機能（区間加算操作と区間最小値取得がしたい！みたいな）が明確になったときに、それを実現するためには atcoder::lazy_segtree の生成時に何を渡せばいいかを考えられるようになることがこの記事の目標です。ただしコンテスト中に読める分量ではなくなったので、整数列に対する単純な機能の組み合わせについてはコピペで使えるチートシート的なものを別途作る予定です。→作りました

対象読者は「セグメント木（抽象化も遅延伝播もナシで可）を書いたことがあって、その構造と動作の仕組みについて何となく理解している人」くらいを想定しています。もちろん遅延伝播の仕組みと内部実装を知っておくに越したことはないので、以下の記事を読んでおくことをオススメします。私もこの記事で勉強しました。

遅延評価セグメント木をソラで書きたいあなたに - hogecoder

また、この記事を書こうと思ったきっかけはお題箱の「AOJのRSQ and RUQをAtcoder Libraryでどう解けばいいか」というリクエストでした。その答えは最後のほうに書いています。

AtCoder Libraryの公式ドキュメント

https://atcoder.github.io/ac-library/document_ja/lazysegtree.html

遅延伝播セグメント木の機能

遅延伝播セグメント木を使うと、整数列などのデータ列 $a_{0}, ..., a_{n-1}$ に対して以下の2つのクエリを処理できるようになります。

区間変更クエリ：指定した区間内のデータ $a_{l}, ..., a_{r-1}$ それぞれに対して、一様に何らかの変更操作を行います。
区間取得クエリ：指定した区間内のデータ $a_{l}, ..., a_{r-1}$ に対して何らかの計算を行った結果を得ることができます。

例えばこういう問題が解けるようになります。

変更クエリ・取得クエリでそれぞれどういう処理を行うかは解きたい問題によって変わります。atcoder::lazy_segtree は生成時にこれらの処理内容をプログラマーが与えることで、1つのライブラリで様々なクエリの組み合わせを実現できるようになっています。これは非常に便利で強力である反面、使い方が難しくなりがちです。この記事ではその使い方を学びます。

またやりたい処理が何でもかんでもセグメント木で扱えるわけではなく、特定の性質を満たしている必要があります。そのことについても終わりの方で説明します。

遅延伝播の仕組み

遅延伝播セグメント木はこんな形をしています。

f:id:betrue12:20200922142356p:plain:h300

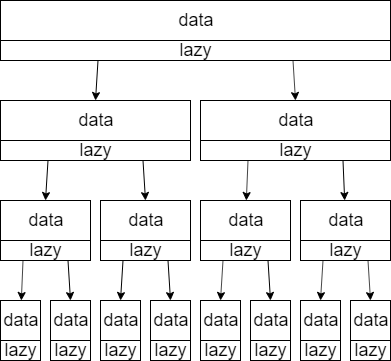
区間を担当する各ノードが data と lazy の2つの値を保持しています。 atcoder::lazy_segtree の内部実装ではそれぞれ d と lz です。

data：一番下のノードは列の各要素を保持する。その上にあるノードは、受け持つ区間の要素に対して取得演算を行った結果（区間最小値取得の機能を持つセグ木なら、その区間の最小値）を保持する。
lazy：その区間に対して行われた操作のうち、まだ自身より下のノードに作用させていないものを保持する。

data は通常のセグメント木と同じです。lazy が遅延伝播のキモで、操作をすぐに全ノードに伝播させず、必要になるまで上側にあるノードが溜めます。逆に言えば各ノードが持っている data は、自身の上にあるノードたちが lazy として溜めている操作が全て降りて来るまでは正確な（最新の）値とは限らない、ということです。

※そのため、もう伝える先がない末端のノードの lazy は実際には不要です。AtCoder Libraryの内部実装でもここの領域は確保されていません。

ある広い区間に対して何度も操作クエリが行われた時、それを末端のノードまで毎回伝えていくと計算量が増えてしまいます。なのでノード全体を覆うような操作はそのノードがずっと溜めておいて、その中のより狭い区間に対するクエリが来たときに初めて下に伝えていく。これが遅延伝播の仕組みです。

f:id:betrue12:20200922195813p:plain

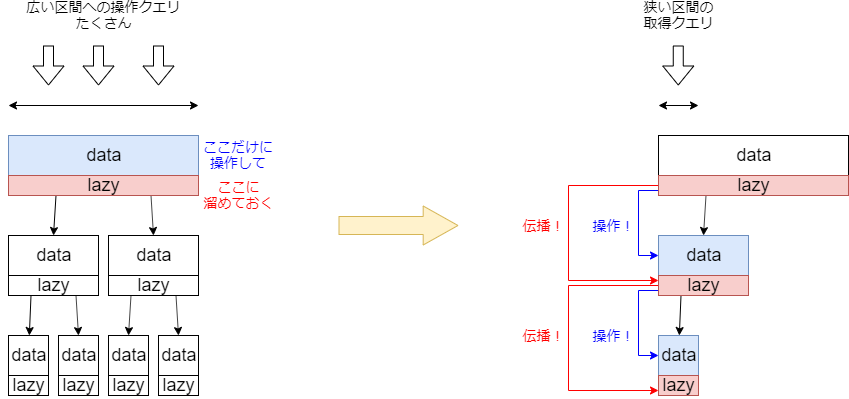
とりあえずここまで理解できればOKです。atcoder::lazy_segtree に渡す型や関数の説明ができるようになります。

テンプレート引数の作り方

atcoder::lazy_segtree のコンストラクタは以下のように定義されています。

(1) lazy_segtree<S, op, e, F, mapping, composition, id> seg(int n);
(2) lazy_segtree<S, op, e, F, mapping, composition, id> seg(vector<T> v);

具体例として「整数の数列に対する、区間加算操作と区間最小値取得」の機能を持つセグメント木を作るために、<> の中のテンプレート引数として何を渡すべきか考えてみましょう。この例にしたのはイレギュラーなパターンが一番少ないからです。

`S` と `F`

S は data、つまり各要素および区間取得結果の型です。整数の数列なら int や long long などです。

F は lazy、つまり操作（写像）を表す値の型です。整数を加算する操作なら同じく int や long long などです。

今回の場合は両方 int とします。int と直接書いても良いですし、using S = int; などと別名を付けて S と書いても良いです。

`S op(S a, S b)`

区間取得をどのような演算で行うかを定義します。通常のセグメント木と同じです。

ドキュメントの使用例にあるように、関数を別途定義してその関数名を引数に書けば良いです。区間最小値取得なら S op(S a, S b){ return std::min(a, b); } を作って op を渡します。ドキュメントの関数名と合わせる必要はありません。

`S mapping(F f, S x)`

操作 f を各ノードが持つ data の値 x に対して作用させる関数です。この mapping と次の composition が、先ほど伝播の仕組みを説明した図においてどこに該当するかを示します。

f:id:betrue12:20200922195827p:plain

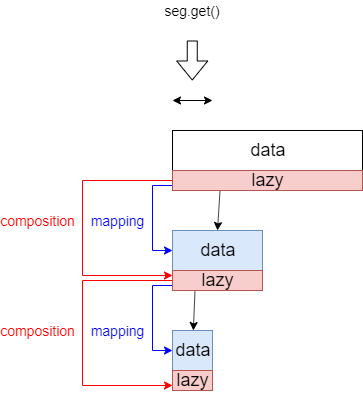
区間加算操作・区間最小値取得の場合を考えます。末端のノードの data は数列の各要素1つに該当するので、加算操作では単に f を x に足せば良いです。ですがここでは「上側のノードが持つ値、つまり既に取得演算をしてしまった値に対して操作しても大丈夫か？」という点に注意する必要があります。

例えば区間 $\lbrack 0, 4)$ を受け持つノードは data として $\min(a_{0}, a_{1}, a_{2}, a_{3})$ の値を保持しています。この区間に対して「区間内の全要素に整数 $f$ を加算する」という操作を行うと、この data の値は $\min(a_{0}+f, a_{1}+f, a_{2}+f, a_{3}+f) = \min(a_{0}, a_{1}, a_{2}, a_{3}) + f$ となります。

同様にどのノードであっても、操作 f を行った時には元々持っていた data の値に f を足せば良いです。そのため mapping の定義は S mapping(F f, S x){ return x+f; } となります。

区間和取得の機能を持たせる場合は少し面倒です。後で説明します。

`F composition(F f, F g)`

既にこれまでの操作を溜めている lazy に対して、さらに新しい操作を追加する関数です。g がこれまでの操作、f が後に追加する操作で、「その2つの操作を順に行うようなひとまとめの操作（合成写像）」を返します。

区間加算操作の場合、「g を足す」という操作の後に追加で「f を足す」という操作は、合わせると結局「f+g を足す」という操作になります。なので composition の定義は F composition(F f, F g){ return f+g; } とします。

今回の場合は足し算が可換な演算なので気にしなくても良いですが、可換でない場合には順番に注意しましょう。f のほうが後の操作です。

`S e()` と `F id()`

それぞれ、区間取得演算 op の単位元と区間操作演算 mapping における恒等写像を返す関数です。関数として渡す仕様になっていますが、この値がプログラムの途中で変わることはほぼないので定数を返す関数を作れば良いです。

二項演算 op の単位元 e とは、全ての a に対して op(a, e) = op(e, a) = a を満たすものを指します。区間最小値取得の場合は「（自身相手でない限り）絶対に最小値として採用されないような値」、つまり $\infty$ とすれば良いです。実装上は data が取り得ないような十分大きな整数を使います。例えば data が最大で $10^{9}$ までの値を取り得る場合、S e(){ return int(1e9)+1; } とすれば良いです。

操作を行う関数 mapping における恒等写像 id とは、全ての a に対してmapping(id, a) = a となるものを指します。区間加算操作の場合は「足しても絶対に対象の値を変えないような値」、つまり $0$ を使います。F id(){ return 0; } とすれば良いです。

よく使う単位元や恒等写像として、最小値であれば $+\infty$ 、最大値であれば $-\infty$ 、和や加算であれば $0$ 、積や乗算であれば $1$ を使えば良いです。更新操作の場合は？恒等写像がないですね。後で説明します。

完成！

これで全部の型と関数が定義できました。以下のように使うことができます。

using S = int;
using F = int;
S op(S a, S b){ return std::min(a, b); }
S e(){ return int(1e9)+1; }
S mapping(F f, S x){ return x+f; }
F composition(F f, F g){ return f+g; }
F id(){ return 0; }

int main(){
    std::vector<int> v = {0, 1, 2, 3, 4};
    atcoder::lazy_segtree<S, op, e, F, mapping, composition, id> seg(v);
}

変数名として使いたい S とか e がグローバルに置いてあると何かと面倒だと思うので、適宜名前は変えて良いです。

注意すべきケース

いくつか注意すべきケースを説明します。

区間和を取る場合の `mapping`

区間加算操作・区間和取得の機能を持たせる場合の mapping の実装を考えます。

区間 $\lbrack 0, 4)$ を受け持つノードの data の値は $a_{0} + a_{1} + a_{2} + a_{3}$ です。ここに「区間内の全要素に $f$ を加算する」という操作を行うと、その値は $a_{0} + a_{1} + a_{2} + a_{3} + 4f$ となるべきです。つまり元々持っていた値に $f \times (区間の幅)$ を足す必要がありますが、mapping の引数では区間の幅が渡されていません。

この場合は公式ドキュメントの使用例に倣い、data のほうに区間の幅を持ちます。例えば data の型 S を

struct S{
    int value;   // 実際の値
    int size;    // 区間の幅
};

という構造体で定義します。末端の要素については data[k].size = 1 として、区間取得の演算を S op(S a, S b){ return {a.value + b.value, a.size + b.size}; } とすれば、各ノードが持つ区間幅が適切に求められます。

これで区間幅が使えるので、区間加算操作は S mapping(F f, S x){ return {x.value+x.size*f, x.size}; } と実現することができます。

注意点として、必ず全要素の size を $1$ にセットした vector を渡して初期化してください。単位元の size は $0$ とするので、要素数を渡して初期化してしまうと全ての data の値が単位元になり、区間幅が全て $0$ になってしまいます。

以上の内容を踏まえた、区間加算操作・区間和取得の機能を持つセグメント木の定義の全体像を示します。

struct S{
    int value;
    int size;
};
using F = int;
S op(S a, S b){ return {a.value+b.value, a.size+b.size}; }
S e(){ return {0, 0}; }
S mapping(F f, S x){ return {x.value+x.size*f, x.size}; }
F composition(F f, F g){ return f+g; }
F id(){ return 0; }

int main(){
    int n = 5;
    std::vector<S> v(n, {0, 1});
    atcoder::lazy_segtree<S, op, e, F, mapping, composition, id> seg(v);
}

応用的な使い方として、例えば座標圧縮をしたことで各末端ノードが受け持っている実際の長さが $1$ とは限らない時も、この size に入れておくと各ノードが受け持つ実際の長さが分かります。操作対象の数列の要素数がクエリ数に対して非常に多い場合に有効です。

区間更新操作の恒等写像

「区間中の値を全てある値 $x$ に更新する」という区間更新操作と、区間和取得の機能を持たせる場合を考えます。この場合恒等写像を表現できる値がないので困ります。

何通りか解決方法があって、「lazy の値として取り得ないような値を擬似的に恒等写像として扱う」方法と、「更新すべき値が存在する（恒等写像でない）かどうかのフラグをbool値で持つ」方法があります。今回は型を変えなくて良い前者を紹介しますが、「その値が lazy として本当に取り得ないか？」という点には十分注意してください。

擬似的に恒等写像として扱う値を ID とします。このとき写像を扱う関数である mapping と composition はそれぞれ以下のようになります。

S mapping(F f, S x)：f が ID ならばそのまま x を返す。そうでなければ区間内の値全てを f に変更するので、x.value = x.size * f とする。
F composition(F f, F g)：f が ID ならばそのまま g を返す。そうでなければ、後からの操作で上書きされるので f を返す。

区間和取得を考える場合、先ほどと同様に区間幅が必要な点に注意してください。

以上の内容を踏まえた、区間更新操作・区間和取得の機能を持つセグメント木の定義の全体像を示します。

struct S{
    int value;
    int size;
};
using F = int;
const F ID = int(2e9);
S op(S a, S b){ return {a.value+b.value, a.size+b.size}; }
S e(){ return {0, 0}; }
S mapping(F f, S x){
    if(f != ID) x.value = x.size * f;
    return x;
}
F composition(F f, F g){ return (f == ID ? g : f); }
F id(){ return ID; }

int main(){
    int n = 5;
    std::vector<S> v(n, {0, 1});
    atcoder::lazy_segtree<S, op, e, F, mapping, composition, id> seg(v);
}

これを用いてAOJの「RSQ and RUQ」を解いたコードが以下です。

Aizu Online Judge

bool値でフラグを持つ場合は、F の型を S と同じように構造体にしたり pair<int, bool> にしたりします。実装はだいたい同じで、最初にフラグを見て恒等写像であれば更新せずに返すという処理をします。

「セグ木に乗る」とは

やりたい演算がセグメント木に乗るとか乗らないとかいう話は、結局のところこれらの関数 op mapping composition を適切に定義できるかどうか？という点に尽きます。単位元と恒等写像はどうにでもなるので。

op は通常のセグメント木にも存在する取得クエリの演算で、これが結合法則を満たすことがまず必要です。この説明はこちらの記事に詳しく書いています。

遅延伝播を行う時にはそれに加えて、以下の2つの性質を満たすような関数を見つける必要があります。

mapping：操作を、全てのノードが持つ data に同じ計算式で作用させることができること。このとき区間幅など必要な情報を data 側に持たせて補うのはOK。
composition：複数の操作を連続して行うという操作（合成写像）を、あたかも1回の操作であるかのように扱って lazy に持たせることができること。

最後に

かなりの分量になりました。セグメント木として実現したい機能をどういう風に分解して関数を作っていけば良いか、理解する助けになれば幸いです。

Practice Contestの問題では2問とも変なものを乗せていますが、まずは整数列に対する単純な演算を実現できるよう色々練習していくのが良いと思います。AOJの区間クエリ問題集などが良いでしょうか。徐々に慣れていって、いずれは変なものを乗せられるようになりましょう。

ARMERIA

Rubyと競技プログラミングの話　AtCoderやCodeforcesの問題解説記事が多め。

AtCoder LibraryのLazy Segtreeの使い方

AtCoder Libraryの公式ドキュメント

遅延伝播セグメント木の機能

遅延伝播の仕組み

テンプレート引数の作り方

`S` と `F`

`S op(S a, S b)`

`S mapping(F f, S x)`

`F composition(F f, F g)`

`S e()` と `F id()`

完成！

注意すべきケース

区間和を取る場合の `mapping`

区間更新操作の恒等写像

「セグ木に乗る」とは

最後に

AtCoder Libraryの公式ドキュメント

遅延伝播セグメント木の機能

遅延伝播の仕組み

テンプレート引数の作り方

S と F

S op(S a, S b)

S mapping(F f, S x)

F composition(F f, F g)

S e() と F id()

完成！

注意すべきケース

区間和を取る場合の mapping

区間更新操作の恒等写像

「セグ木に乗る」とは

最後に

`S` と `F`

`S op(S a, S b)`

`S mapping(F f, S x)`

`F composition(F f, F g)`

`S e()` と `F id()`

区間和を取る場合の `mapping`