2020-05-02

パソコン甲子園2019本選 (AOJ 0426) 三角形の個数の和

AOJ プログラミング競技プログラミング

お題箱より。

Aizu Online Judge

解いてなかったのでこのリクエストを見て解きました。

解法

言い換えを重ねる

全ての点の個数を $N = (H+1)(W+1)$ と表記することにします。

「全ての点集合について、その集合に含まれる三角形を数えて合計する」を、「全ての三角形をなす3点の組み合わせについて、それを含む点集合を数えて合計する」と言い換えます。

そうすると3点の選び方に依らず、それを含む集合は「その3点は必ず含み、残りの $N-3$ 点について含む/含まないを自由に選ぶ」ことになるので $2^{N-3}$ 通りあります。

そのため、三角形をなす異なる3点の選び方の数が分かれば良いです。その代わりに三角形をなさない（つまり一直線上にある）異なる3点の選び方の数を求めて、制限を設けない異なる3点の選び方の数 $_{N}C_{3}$ から引くことにします。

一直線上にある3点の選び方

というわけで求めるものは、一直線上にある異なる3点の選び方の数となりました。これの求め方ですが、両端になっている2点間の $y$ 座標・ $x$ 座標の差の組み合わせを全探索します。これらをそれぞれ $i, j$ とします。（ $i = j = 0$ は除外）

このとき反転させて同じになるものは重複しないように注意する必要があります。1つの手段としては、「 $i \ge 0$ かつ $j \ge 0$ の範囲を探索し、 $i \gt 0$ かつ $j \gt 0$ のものについては傾き反転のぶん2倍する」などとすると良いです。

$(i, j)$ を固定したら、まず領域内で両端として取れる場所が何通りあるかを計算します。これは $(H+1-i)(W+1-j)$ になります。

その上で、間に位置する3点目が何通り取れるかを計算します。これは $\gcd(i, j)-1$ になります。例えば $(i, j) = (4, 8)$ の場合、間の点は $(1, 2), (2, 3), (3, 6)$ の位置に相当する3通りです。

f:id:betrue12:20200502163308p:plain

これで、一直線上にある異なる3点の選び方の数を求めることができました。あとはこれまでの解説を巻き戻るように計算していけば、答えを求めることができます。

ACコード

Aizu Online Judge

2020-05-02

Codeforces Round #614 (Div. 1) C. Xenon's Attack on the Gangs

Codeforces プログラミング競技プログラミング

お題箱より。

Problem - C - Codeforces

問題概要

$n$ 頂点の木が与えられる。この木の辺に $0, 1, ..., n-2$ の値を1つずつ割り振ることを考える。

異なる2頂点 $u, v$ に対して $mex(u, v)$ を「 $u, v$ 間パスに含まれる辺の値として登場しない最小の非負整数」と定義する。そして値の割り振り方のスコア $S$ を

$S = \displaystyle \sum_{1 \le u \lt v \le n} mex(u, v)$

と定義する。 $S$ の最大値を求めよ。

制約

$2 \le n \le 3000$
与えられるグラフは木である

解法

スコア $S$ は、以下の値を全て合計したものとして計算できます。

$s_{1} =$ パスに $0$ を含む2頂点のペアの個数
$s_{2} =$ パスに $0, 1$ を含む2頂点のペアの個数
$s_{3} =$ パスに $0, 1, 2$ を含む2頂点のペアの個数
....

なぜなら $mex(u, v)$ がある値 $k$ である必要十分条件は、 $u, v$ 間のパスに $0, 1, ..., k-1$ が全て含まれていてかつ $k$ が含まれていないことであり、このようなペアは上記の計算方法で $s_{1}, ..., s_{k}$ のちょうど $k$ 回数えられるからです。

スコアをなるべく大きくするには、値 $0, 1, 2, ...$ を割り振る辺をなるべく一直線に並べるのが得策です。具体的には

どこかの辺に値 $0$ を割り振る。
値 $1$ の辺は、値 $0$ の辺の両端どちらかに接続する辺から選ぶ。
値 $2$ の辺は、値 $0, 1$ の辺で作られるパスの両端どちらかに接続する辺から選ぶ。
...

という割り振り方を、パスの両端をもう伸ばせなくなる（つまり両端がともに葉である）まで続けるのが良いです。このような形になっていないもの、つまりまだパスを伸ばせるのに途中で非連結になったり枝分かれしているような割り振り方は、パスになるように組み替えることで解をより良くできることが示せます。

f:id:betrue12:20200502143837p:plain

値の割り振りルールをこのようなものに限定できることを利用して、スコアの最大値を求めるDPを考えます。アイデアは「短いパスから始めてだんだん長くしていく」という感じです。具体的には2頂点 $u, v$ に対して $dp\lbrack u \rbrack\lbrack v \rbrack$ を以下のように定義します。

頂点 $u, v$ 間のパスに含まれる辺を $d$ 本として、このパスの辺に $0, ..., d-1$ の値を割り振った時に得られる $s_{1} + \cdots + s_{d}$ の最大値

これを $d$ が小さいような2頂点ペアから順番に計算していきます。メモ化再帰でも良いでしょう。

$dp\lbrack u \rbrack\lbrack v \rbrack$ を計算する遷移を考えます。ここで $s_{d}$ の値は、パスによって分断された部分木を考えると「 $u$ 側の部分木に属する頂点の個数」×「 $v$ 側の部分木に属する頂点の個数」として計算できます。その前の $s_{1} + \cdots + s_{d-1}$ はDPの遷移元であり、その値は

$u$ 側に値 $d-1$ の辺を置く場合、 $u, v$ 間パスにおける $u$ の隣の頂点を $u^{\prime}$ として $dp\lbrack u^{\prime} \rbrack\lbrack v \rbrack$
$v$ 側に値 $d-1$ の辺を置く場合、 $u, v$ 間パスにおける $v$ の隣の頂点を $v^{\prime}$ として $dp\lbrack u \rbrack\lbrack v^{\prime} \rbrack$

のどちらかなので、大きい方を持ってくれば良いです。

f:id:betrue12:20200502150106p:plain

このDPの計算では、パス $u, v$ について

相手が $v$ であるときの、パスで分断された $u$ 側の部分木のサイズ
相手が $v$ であるときの、パスにおける $u$ の隣の頂点

の情報（と、その逆）が必要になります。これは $v$ を根とするDFSで計算することができて、特にパスにおける隣の頂点は親になります。あらかじめ全ての頂点を根とするDFSを回して前計算してしまいましょう。

全ての $dp\lbrack u \rbrack\lbrack v \rbrack$ の最大値が答えになります。DPも前計算も計算量はともに $O(n^{2})$ です。

ACコード

Submission #69183992 - Codeforces

2020-05-01

AtCoder Grand Contest 037 A - Dividing a String

AtCoder プログラミング競技プログラミング

お題箱より。

A - Dividing a String

貪欲とDPどちらを書こうか迷いましたが、貪欲解法のほうで書きたいと思います。

問題概要

文字列 $S$ が与えられる。この $S$ をできるだけ多くの部分文字列に分割したい。ただし、隣り合う2つの部分文字列が一致してはならない。

最大でいくつの部分文字列に分割できるか答えよ。

※以降の解説では文字列 $S$ の長さを $N$ と表記します。

解法

貪欲法、つまり前からできるだけ短い文字列で切っていくという手順で解く方法を試してみましょう。

ルール1：前から文字列を見て、なるべく1文字ずつ切っていく。ただし「直前に1文字で切っていて、かつ今から見る文字がその文字と同じ」という時だけ2文字で切る。

このルールで入力例2の aaaccacabaababc を切ると以下のようになります。数えると出力例と同じ12分割です。

f:id:betrue12:20200501194723p:plain

ただしこれだけのルールだと、入力例1の aabbaa や aaaaa などのケースで困ります。

f:id:betrue12:20200501195034p:plain

このように最後に残った2文字が同じ場合、貪欲に1文字で切ると最後に残った1文字と等しくなってアウトです。このようなケースのために、末尾2文字を見る時だけ次のルールを課します。

ルール2：最後に2文字残り、それらが同じである場合、その2文字をそのまま採用する。もしその2文字も直前に切った2文字の文字列と一致してしまう場合、その4文字を3+1文字と割り振る。

3+1文字になるのは以下の図のような場合です。

f:id:betrue12:20200501195303p:plain

結論を言ってしまうとこれで最適な分割方法を実現できるので、前からシミュレーションすると正解を求めることができます。

ただ貪欲法にありがちなこととして、このような貪欲で解けると仮説を思いつくことよりも、その正しさを証明することのほうが難しいです。証明しましょう。

証明

先ほどの貪欲ルールで2文字または3文字になってしまったところには、それぞれ原因となった「同じ文字が隣接している箇所（以下、原因箇所）」が存在します。貪欲ルールで得られた分割数が $a$ である場合、全部1文字で切れた場合と比べて損をした $N-a$ と同じ数だけこの原因箇所が存在します。

f:id:betrue12:20200501195837p:plain

ルール2で3+1になっている場合は以下のように考えると原因箇所が2つあります。

f:id:betrue12:20200501200317p:plain

このように入力が aaaaa... と最も厳しい場合でも、貪欲ルールでは1+2+1+2+...のような切り方ができるので、この原因箇所は少なくとも1文字の間を空けて並んでいるはずです。

どのような切り方であっても、この原因箇所を挟んでいる2文字を両方とも1文字で切ることは条件違反なのでできません。また、2文字の文字列を1つ作ることで2箇所の原因箇所を潰すこともできません。原因箇所を潰すためには、原因箇所1つにつき2文字以上の文字列を1つ作るか、複数の原因箇所を潰すために長い文字列を作る必要があります。つまり原因箇所1つにつき少なくとも1文字ぶん損をする必要があります。

ここで貪欲ルールは「原因箇所1つにつきちょうど1文字ぶんだけ損をしている」切り方になっていました。これは実現できるギリギリの損の数です。よって、貪欲ルールによる分割数は最適であるということが示されました。

ACコード

Submission #12541470 - AtCoder Grand Contest 037

「直前が1文字であるかどうか」のフラグを持ってシミュレーションします。最後にルール2に引っかかる場合は、どちらのケースであっても「最後の2文字を使って分割個数が1増える」と見なすことができるので、実装上は区別する必要ないです。

おまけ：DPの場合

DPのほうが正当性を証明するのは楽なのですが、DPそのものへの慣れが必要なので今回の記事では見送りました。

DPの場合でも全くの無考察で解けるわけではなく、計算量を削減するためには「最適解に登場する部分文字列の長さは長くならない」という考察をする必要があります。またこれを文字数だけで容易に証明できるのは「最適解に登場する部分文字列は4文字以下である」というところまでで、公式解説や多くのDP解法記事で書かれている「2文字以下」というところまで示すには結局さっきの貪欲法と同じようなことを考える必要があります。なので、証明の理解まで含んだ時に最も易しい解法は「4文字以下まで絞ってDP」だと思います。

証明も書いておきます。ある分割方法に5文字の部分文字列が存在すると仮定します。5文字の部分文字列をさらに、文字数の異なる2つの部分文字列に分割することを考えます。この方法は1+4, 2+3, 3+2, 4+1の4通りあって、そのうち前とも後ろとも隣接する部分文字列の文字数が一致しないものが少なくとも2通り存在します。つまり、この分割方法はさらに分割数を増やすことができるので最適ではありません。

6文字以上の部分文字列を含む分割方法も、同様の手順で最適ではないことを示せます。よって「最適解に登場する文字列は4文字以下である」ことが示されました。

2020-04-23

Codeforces Round #501 (Div. 3) F. Bracket Substring

Codeforces プログラミング競技プログラミング

お題箱より。

Problem - F - Codeforces

問題概要

整数 $n$ と、開き括弧・閉じ括弧からなる文字列 $s$ が与えられる。長さ $2n$ の正しい括弧列であって、その連続部分文字列として $s$ をどこかに含むものの個数を $\bmod 10^{9}+7$ で求めよ。

制約

$1 \le n \le 100$
$1 \le |s| \le 200$

解法

DPを立てる

正しい括弧列の問題は、( を $+1$ 、) を $-1$ とした累積和を考えるのが定石です。先頭からの累積和がどの時点でも負にならず、かつ最後に $0$ になるものが正しい括弧列です。

今回のように制約が小さく、「数学で一発」みたいな解法が考えづらい場合、以下のようなDPを考えることが多いです。

$dp\lbrack i \rbrack\lbrack j \rbrack\lbrack ? \rbrack =$ 先頭 $i$ 文字までを作って、その時点までの累積和が $j$ で、かつ○○が $?$ であるものの個数。

正しい括弧列の条件を守るため、 $j$ が負のところには遷移しないようにして、最終的に $j=0$ のものだけを答えとして採用します。

$?$ の部分に問題特有の条件が入ってきます。今回の問題の場合は「連続部分文字列として $s$ をどこかに含むもの」なので、追加で必要な状態をこのように設定します。

$dp\lbrack i \rbrack\lbrack j \rbrack\lbrack k \rbrack\lbrack f \rbrack =$ 先頭 $i$ 文字までを作って、その時点までの累積和が $j$ で、かつ直近 $k$ 文字が $s$ の先頭 $k$ 文字と一致していて、かつこれまでの文字列の中に既に $s$ が含まれている（ $f=1$ ）/いない（ $f=0$ ）ものの個数。

※より厳密に書くと、「『直近 $x$ 文字が $s$ の先頭 $x$ 文字と一致している』という条件を満たす最大の $x$ が $k$ である」のほうが正しいです。例えば $s$ が ()() の場合、()( は $k=0,1,3$ に対して先ほどのことが成り立ちますが、マッチするもののうち最も長いものを取って $k=3$ にだけ算入します。

添字が2個増えました。まず $k$ については「今どこまで $s$ にマッチしているか」を表します。そして $f$ は言わば「クリア済みフラグ」で、1度でも $s$ が完成したら $f=1$ にして遷移します。こうすれば最後に、正しい括弧列かつ1度以上 $s$ が登場するものを数えることができます。

各遷移では開き括弧と閉じ括弧の両方を試します。このとき $s$ が $k$ 文字まで一致しているので、その続きとして正解のほうの文字であれば $k+1$ に遷移すれば良いですが、異なるほうの文字だったらどうすれば良いでしょう？これは単に「全部やり直し」で $k=0$ に遷移するわけではなく、もう少し考える必要があります。

$k$ の遷移を考える

具体例を示します。 $s$ が ()(() だったとしましょう。これまで作った文字列が ()( であったとき、これは累積和が $+1$ で直近 $3$ 文字が $s$ の先頭と一致しているので状態としては $dp\lbrack 3 \rbrack\lbrack 1 \rbrack\lbrack 3 \rbrack\lbrack 0 \rbrack$ に属しています。

ここで ( を付けて ()(( とすると、これは $s$ の続きとして「正解」なので $k$ が1つ増えて $dp\lbrack 4 \rbrack\lbrack 2 \rbrack\lbrack 4 \rbrack\lbrack 0 \rbrack$ に遷移します。

一方 ) を付けて ()() とした場合、今まで続けてきた $s$ は途切れます。ですが改めて見ると直近 $2$ 文字について $s$ の先頭と一致しています。つまりこの場合 $dp\lbrack 4 \rbrack\lbrack 0 \rbrack\lbrack 2 \rbrack\lbrack 0 \rbrack$ に遷移する必要があります。

この遷移を実現するために必要なのは、「 $s$ の先頭 $k$ 文字が完成している状態で、この文字を付け加えると、その後は最大何文字マッチしている状態になるか？」という値を前計算することです。正解のほうは $k+1$ になりますし、そうでないほうは実際に試してみることになります。 $O(n^{3})$ 掛けて良いので地道に全部試してOKです。

これでDPが回せるようになります。最終的な答えは、全ての $k$ について $dp\lbrack 2n \rbrack\lbrack 0 \rbrack\lbrack k \rbrack\lbrack 1 \rbrack$ を合計したものです。

ACコード

Submission #77758062 - Codeforces

なお $f=1$ になって以降は $k$ の値は意味を持たなくなるので、添え字から $f$ を削り、いったん $s$ が完成したものは常に $k=|s|$ とするような遷移を組んでも大丈夫です。少し定数倍が良くなります。

2020-04-23

AtCoder Beginner Contest 162 F - Select Half

AtCoder プログラミング競技プログラミング

お題箱より。

F - Select Half

前置き

リクエストでは「そもそもなぜDPを思いつくのか」を知りたいという声をもらったのですが…この点は非常に難しいと思っています。というのも、私の場合はDPで最終的に解けない問題であっても考察途中で「DPできないか？」ということを考えているからです。同じように「貪欲できないか？」「二分探索できないか？」なども多くの問題で考えます。

どちらかというと「仮にDPに落とし込んだとしたらどういう状態が持てるだろう？」と考える習慣を付けるのがオススメです。思いつかなかったり、計算量的に間に合わないDPしか思いつかないなら一旦他の方針に頭を切り替えて良いです。それがたとえハズレ方針であっても、考察の引き出しを増やしてその中から適切な方針を選ぶ力に繋がります。

実際に私はこの問題で、最初にDPではない方針を考えて途中まで実装もしてしまっていました。結果的にタイムロスになりましたが、「こっちの解法ではダメ」という理由も含めて理解できたので後でDPにしっかり切り替えられたと思います。「試しに仮説を立てて考えてみる」ことがとても大事です。

解法

数列に対するDPで最も基本となるのは「左から順に見ていく」DPです。今回は要素を選ぶ条件として「個数」「選んだ要素同士の間隔」が制限されているため、これらを判断できるような情報をDPテーブルに盛り込みます。例えば以下のようなものです。

$dp\lbrack i \rbrack\lbrack j \rbrack =$ 最後に選んだ要素が $a_{i}$ であって、選んだ個数が $j$ 個であるときの、選んだ要素の和の最大値

これは間に合わないので、この問題の性質を使って改良しましょう。

実際に数を並べて、問題の条件を満たすように要素を選ぶ方法をいくつか考えてみます。必ず1つ間隔を空けるというルールでだいたい半分の要素を選ぶので、ほとんどの場所では「ちょうど1個」間隔が空いていることになります。そして1個より多く間が空いているところはそんなにたくさん作れません。

選ぶ位置と選ばない位置をボールのように図示すると、具体的には以下のようになります。

f:id:betrue12:20200422235344p:plain

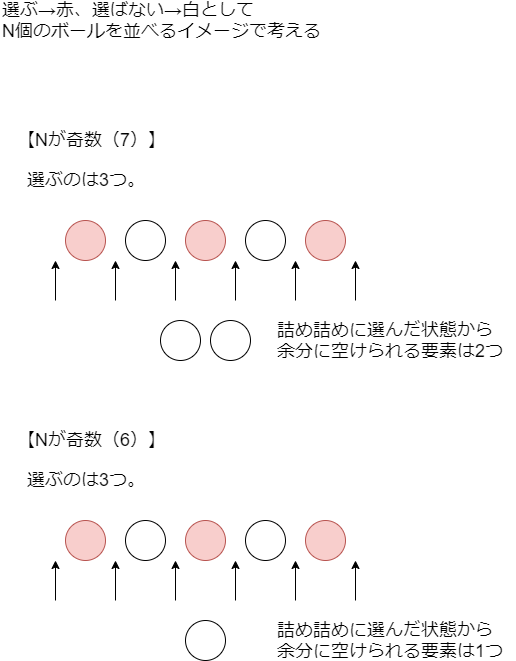
つまり先ほど試しに立てたDPで

$dp\lbrack i \rbrack\lbrack j \rbrack =$ 最後に選んだ要素が $a_{i}$ であって、選んだ個数が $j$ 個であるときの、選んだ要素の和の最大値

としましたが、実際に起こり得る状況ではこの $j$ はほぼ $\frac{i}{2}$ に近い値になって、例えば $dp\lbrack 100 \rbrack\lbrack 0 \rbrack$ とか $dp\lbrack 100 \rbrack\lbrack 99 \rbrack$ みたいな値は考えなくていいということが分かります。これが公式解説で言う「無駄」の意味です。

では何を持てば良いかというと、旧DPの $j$ が $\frac{i}{2}$ に近いことを利用し、その誤差を意味するような値を持てば良いです。今回は先ほどの図で記した「詰め詰めの状態に比べて余分に空けた要素数」を持つことにします。

$dp\lbrack i \rbrack\lbrack j \rbrack =$ 最後に選んだ要素が $a_{i}$ であって、詰め詰めの状態に比べて余分に空けた要素数が $j$ 個であるときの、選んだ要素の和の最大値

この場合は $j$ として2以下の値しか考えなくて良いので、状態数が少なくなります。

$dp\lbrack i \rbrack\lbrack j \rbrack$ からの遷移を考えます。 $a_{i}$ の次に $a_{i+2}$ を取るのは「詰めている」状態なので、 $dp\lbrack i+2 \rbrack\lbrack j \rbrack$ に遷移。 $a_{i+3}$ を取ると「1個余分に空けた」状態なので $dp\lbrack i+3 \rbrack\lbrack j+1 \rbrack$ に遷移…という風に考えれば良いです。

端の要素を空ける場合の処理などが少し面倒ですが、この考え方でDPを組むことができます。

今回の問題では「1個以上間隔を空けておよそ半分の要素を選ぶ」という制限がけっこう強いものであり、あまり好き勝手に要素を選べないことを利用して、状態数の少ないDPを考えることができました。一度間に合わないDPを考えてから「無駄」に気付くか、先に考察を進めてからDPに落とし込むか。どちらが先でも良いですが、「DPできないかな？」と「何か良い性質無いかな？」という2つの視点が必要です。引き出しを増やし、どんどん仮説を立てて問題を解いていきましょう。

ACコード

Submission #11832539 - AtCoder Beginner Contest 162

2020-04-22

Codeforces Round #636 (Div. 3) F. Restore the Permutation by Sorted Segments

Codeforces プログラミング競技プログラミング

Problem - F - Codeforces

問題概要

長さ $n$ の順列 $p_{1}, ..., p_{n}$ がある（与えられない）。この順列に対して、 $r=2, ..., n$ それぞれに対して以下のように計算される $n-1$ 個の数列が与えられる。

各 $r$ に対して、 $l \lt r$ なる $l$ を選び、 $p_{l}, ..., p_{r}$ をソートした数列。

ここで $n-1$ 個の数列は並べ替えられた順番で与えられる。

この与えられる $n-1$ 個の数列と矛盾しないような順列 $p_{1}, ..., p_{n}$ を1つ求めよ。そのような順列が1つ以上存在することは保証される。

制約

マルチテストケースであり、ケース数 $t \le 100$
各ケースについて $2 \le n \le 200$ であり、全ケースの $n$ の合計は $200$ を超えない
与えられる数列は上記の条件を満たし、解が1つ以上存在する

解法

正解の順列と与えられる数列の位置関係を図示すると、例えば以下のようになっています。

f:id:betrue12:20200422145338p:plain

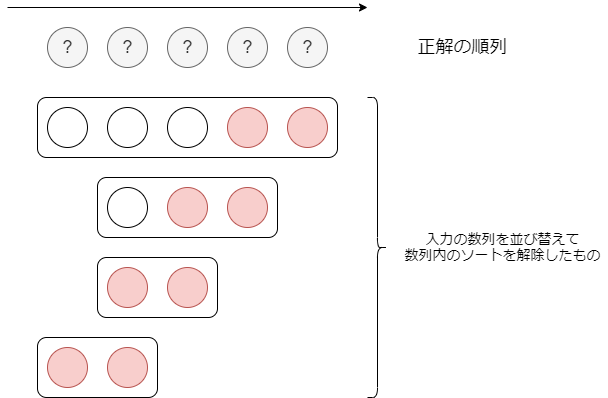
各数列の長さはテストケースに依りますが、赤丸の位置は必ず存在します。

実際には入力の数列のうちどれがどの位置に対応するのかも、各数列の中身が元々どう並んでいたのかも分かりません。なのでこれらに依存しない情報である、「 $1, ..., n$ の各値が入力の数列に合計何回登場するか」に注目します。すると

目標の順列で末尾にある値は、必ず登場回数が1回である。
目標の順列で末尾でも先頭でもない値は、必ず登場回数が2回以上である。

ということが言えます。

そのため登場回数が1回であるような値は1種類または2種類であるはずです。このうち1つを正解の順列の末尾にある値だと仮定することにします。

この末尾の値が含まれている数列について、その中にある値の登場回数をそれぞれ減らします。そうすると正解の順列で末尾から2番目にある値の登場回数が1回になります。

f:id:betrue12:20200422145847p:plain

これで登場回数1回になる値を採用して、その値が含まれている数列について各値の登場回数を減らして…を繰り返したいところですが、上図のように先頭の値も途中で登場回数が1回になる可能性があります。このように処理の途中で2択を迫られると面倒です。

そのため最初の時点で、正解の順列の末尾の値（高々2通り）と先頭の値（末尾以外の $n-1$ 通り）を決め打ちしてしまいましょう。そうすると、各ステップでは「登場回数が1回になった値のうち先頭の値でないもの」を選べばよく、これは高々1種類です。

1回のシミュレーションを $O(n^{2})$ や $O(n^{2}\log n)$ などで行うことができれば実行時間としては間に合います。これでシミュレーションを進め、途中で値の候補がなくなったり、構築できても条件に矛盾するような場合はハズレです。最後まで順列を構築できてかつ全ての条件を満たせば、それを出力して終了します。

ACコード

Submission #77549500 - Codeforces

2020-04-20

AtCoder Beginner Contest 163 F - path pass i（マージテク解法）

AtCoder プログラミング競技プログラミング

F - path pass i

公式解説とは違う方法で、計算量は $O(N(\log N)^{2})$ であまり良くないのですが、私が解いた解法をまとめておきます。

解説

「通らないもの」を数える

頂点数が $N$ であるとき、単純パスの総数は $\frac{N(N+1)}{2}$ 個です。色 $c$ について解く時には、この総数から「色 $c$ の頂点を通らないもの」の個数を引くことにします。

色 $c$ の頂点を除いて木をいくつかの部分木に分解すると、異なる部分木間のパスは必ず色 $c$ の頂点を含みます。そして各部分木の内部で、頂点数 $n$ とすると色 $c$ の頂点を通らない単純パスが $\frac{n(n+1)}{2}$ 個できます。これを合計すれば良いので、つまり各色についてその色の頂点で切ってできる各部分木のサイズが分かれば良いです。

今回はこれを全ての色について計算する必要があり、色ごとに木DPなどをしていては間に合いません。なので全ての色についての計算を一気にしてしまいます。

全色一気に処理するDP

適当に根を決めて木DPを行い、以下の2つの値を管理することにします。

$cnt\lbrack i \rbrack =$ 頂点 $i$ 以下の部分木の頂点数。
$dp\lbrack i \rbrack\lbrack c \rbrack =$ 頂点 $i$ 以下の部分木において、頂点 $i$ の親方向から見て色 $c$ で塞がれているような頂点の個数

後者がちょっと分かりにくいので図で具体例を示します。

これを用いて部分木のサイズを集めていきます。ポイントとしては、頂点 $i$ について見る時には色 $c_{i}$ で区切られた部分木だけが閉じられるということです。具体的には、子 $j$ の方向から伸びてきて頂点 $i$ で閉じられるような部分木の頂点数は $cnt\lbrack j \rbrack - dp\lbrack j \rbrack\lbrack c_{i} \rbrack$ と計算できます。これを集めていけば良いです。

ただしこのように「上から閉じて数える」方法だと根を含む部分木は集計されないので、最後に全ての色について根を含む部分木の個数を計算します。

この $dp\lbrack i \rbrack\lbrack c \rbrack$ を計算する遷移を考えます。これは子のものを全て $dp\lbrack i \rbrack$ に足していって、 $dp\lbrack i \rbrack\lbrack c_{i} \rbrack$ は $cnt\lbrack i \rbrack$ で上書きすればOKです。

この $dp\lbrack i \rbrack\lbrack c \rbrack$ を全ての頂点×全ての色について計算しようとすると間に合いません。しかし頂点 $i$ 以下の部分木に含まれている色の数は $cnt\lbrack i \rbrack$ 種類以下なので、 $dp\lbrack i \rbrack$ を map 等で持ってしまいましょう。そうすると足し合わせていく処理において、俗称「データ構造をマージする一般的なテク」と呼ばれるテクニックが利用できます。長いのでマージテクと呼びます。

マージテクとは

マージテクとはデータ構造（C++で言うと vector や set や map など）で保持したデータを「必ずサイズの小さい方から大きい方にマージするようにする」というルールでマージすることで操作全体の計算量を改善するテクニックです。

今回のケースでは、最初に $N$ 個の各頂点がそれぞれ「サイズ $1$ 」のデータ構造を持っています。これを子から親にマージすることを繰り返して、最終的に根で「サイズ $N$ 」のデータ構造を作ります。（実際には同じ色がある場合は消えますが）

このような時にマージの順序を気にせずに子から親にデータを移してしまうと、データ1個を移動する回数の合計は最大で $O(N^{2})$ 回になってしまいます。根から一直線に伸びるようなグラフがその例です。

ここで「小さい方から大きい方に」のルールを守るために「子の $dp\lbrack j \rbrack$ から親の $dp\lbrack i \rbrack$ にマージするときに、 $dp\lbrack j \rbrack$ のほうが大きければ事前にスワップする」という処理を入れることで、なんとデータ1個を移動する回数の合計が全部で $O(N\log N)$ 回になります。

この計算量は、「1回のマージで移動する要素の個数」ではなく「ある1つの要素が操作全体で移動する回数の合計」に注目すると説明できます。要素が移動する際には元いたデータ構造よりサイズが大きいものに移動するので、「その要素が所属しているデータ構造のサイズ」が2倍以上になります。移動1回ごとにサイズが2倍以上になるという条件で最初のサイズ $1$ から最後のサイズ $N$ になるので、その移動回数は $\log_{2} N$ 以下になります。これが全ての要素について言えるので、全体での移動回数合計が $O(N\log N)$ になる、という仕組みです。

ここで「データ構造」「データ」等の書き方をしていますが、最初に書いたように vector や set や map やその他色々なデータ構造でこのテクニックは利用可能です（「一般的な」と呼ばれている理由です）。1つずつ要素を取り出して移し替えていく、という操作ができるものなら何でもできます。ただしその移動1回の計算量が移動回数合計と掛け算されるので、例えば map を用いると操作全体の計算量としては $O(N(\log N)^{2})$ になります。

まとめ

これで全ての色について、その色の頂点で切ったときの各部分木のサイズが求められ、冒頭に書いた計算式で答えを計算できます。

ここで各色の部分木の総数が異常に増えてしまわないかというのも気になりますが、大丈夫です。ある頂点を取り除いたときに部分木の個数はその次数-1だけ増えるので、部分木の個数を全ての色について足した総数も全頂点の次数の合計、つまり $O(N)$ で抑えられます。

ACコード

Submission #12130625 - AtCoder Beginner Contest 163