2019-06-06

AtCoder Regular Contest 094 E - Tozan and Gezan

AtCoder プログラミング競技プログラミング

お題箱より。

E - Tozan and Gezan

解法

プレイヤーを以下のように表記します。

Aさん: $A_{i}$ を操作する。先攻。ターン数を最大化したい。
Bさん: $B_{i}$ を操作する。後攻。ターン数を最小化したい。

また、 $S = \sum_{i} A_{i} = \sum_{i} B_{i}$ と表記することにします。

もしゲーム開始時点で全ての $i$ について $A_{i} = B_{i}$ だった場合、ゲームは即座に終了し答えは0です。

そうでない場合は和が一定であるという条件から、 $i=1, ..., N$ は以下のグループに分けられます。

グループX: $A_{i} \lt B_{i}$ であるもの。1箇所以上存在する。
グループY: $A_{i} = B_{i}$ であるもの。存在しないかもしれない。
グループZ: $A_{i} \gt B_{i}$ であるもの。1箇所以上存在する。

Aさん→Bさんの順番で、どのような行動を取るのが良いのかを考えていきましょう。

Aさんの行動

Aさんはターンを最大化したいので、 $A_{i}$ と $B_{i}$ をなるべく離すように動かしたいです。そのためZグループにはなるべく触らずに、まずはグループXとYの $A_{i}$ を全て0になるまで減らすのが良さそうです。

その後は仕方がないのでZグループに手を付けますが、ここでの最適手順はどうなるでしょうか。ここで「何が最適か」と考えるとなかなか難しいのですが、少し発想を変えて「このような戦略で動けば、ターン数が必ず○○以上になることが保証できる」ということが言えるような戦略がないか、と考えてみましょう。

全ての値が一致しないとゲームが終わらないこと、Zグループにおいて $B_{i}$ のほうから増えて近づいてくることはあり得ないことから、Zグループに含まれる $i$ のうちどれか1つでも $B_{i}$ と一致させないようにしていればゲームが終わることはありません。

つまりZグループに含まれるインデックスから何か1つ選んで $k$ とし、 $A_{k}$ を最後まで動かさないようにすることで、Aさんは少なくとも $S - B_{k}$ 回以上のターン数を稼げるということになります。

この値をなるべく大きくするには、Zグループの中で $B_{k}$ が一番小さいものを選べば良いです。以降はこのような $k$ を単に $k$ と表記します。

Bさんの行動

Bさんは天才なので、先ほどのAさんの戦略をBさんも理解しています。Bさんがどのように動いても $S - B_{k}$ 回以上のターン数を稼がれてしまうことは分かっています。

つまりBさんにとっては、もし自分が適切に行動することでターン数をちょうど $S - B_{k}$ 回にすることができれば、それが最適だということが分かります。そしてそのような戦略は確かに存在します。

具体的には、Bさんも $B_{k}$ を最後まで触らずに他の $B_{i}$ を0になるまで操作し続ければよいです。このときの合計操作回数は $S - B_{k}$ 回であり、Bさんが最後の操作をした後に

インデックス $k$ 以外については $A_{i} = B_{i} = 0$
インデックス $k$ については $A_{k} = B_{k} = (B_{k} の初期値)$

という状態になり、ゲームが終了します。

そのため答えは $S - B_{k}$ となります。

ACコード

Submission #5807018 - AtCoder Regular Contest 094

なかなか解説を書くのが難しいですね…解説放送でも「答えを言うのは簡単だけど、分かるように解説するのは難しい」と言われていました。

思いつき勝負の面が強い問題ですが、ゲーム問題で直接最適性を考えるのが難しいときに、「このような戦略で動けば利得が必ず○○以上になることが保証できる」ような戦略はあるだろうか？と考えることは、他の問題でも使える可能性があるテクニックだと思います。

2019-06-05

Chokudai SpeedRun 002 K - 種類数 β

AtCoder プログラミング競技プログラミング

お題箱より。

K - 種類数 β

解法

この問題はグラフとして捉えると見通しが良くなります。それぞれの整数を頂点とし、ペア $(a, b)$ を頂点 $a$ と頂点 $b$ を結ぶ辺として考えます。整数を選ぶことを頂点に色を塗ることに喩えると、各辺ごとに「両端の頂点のうちどちらかを選んで色を塗る」という操作をして、最終的に色が塗られた頂点の数を最大にすればよいです。

このグラフで非連結な頂点（数字）同士は互いに関係しないので、それぞれの連結成分ごとに考えます。

連結成分に閉路がない場合

すなわち木になっている場合。このときは連結成分の頂点数 $n$ とすると辺数が $n-1$ 本であり、全ての頂点を選ぶことはできません。

ある1頂点 $i$ を諦めることにすると、各辺について $i$ から遠い方の頂点を選ぶことで必ず $n-1$ 個の頂点に色を塗ることができます。そのためこの連結成分によって答えに $n-1$ が加算されます。

f:id:betrue12:20190605212622p:plain

連結成分に閉路がある場合

まず $(1, 2), (2, 3), (3, 1)$ のような単純な閉路である場合を考えましょう。この場合は $1, 2, 3$ のように順繰りに選んでいくことで全ての頂点に色を塗ることができます。

そうとは限らない、どこかに閉路がある連結成分を考えます。このグラフの全ての頂点は、辺をいくつか選ぶことで

ある1つの閉路
その閉路内の頂点から木のように広がっていく部分たち

で覆うことができます。閉路が複数ある場合はいくつかの辺が無駄になりますが構いません。

このグラフで、まず閉路内の頂点を順繰りに選び、残りの辺で閉路から遠い方の頂点を選んでいくことで、全ての頂点に色を塗ることができます。

f:id:betrue12:20190605213024p:plain

これで連結成分ごとに何個の頂点に色を塗れるかが分かるので、それらを合計すれば答えです。実装は座標圧縮＋Union-Findでできます。

ACコード

Submission #5577663 - Chokudai SpeedRun 002

シンプルな問題ですし、公式解説とほぼ同じですね。公式解説は辺に向きを付けて、辺が入っているほうの頂点（整数）を選ぶとみなす、と考えています。この記事では色を塗ると喩えてみました。お好きな方でどうぞ。

2019-06-05

AtCoder Grand Contest 034 E - Complete Compress

AtCoder プログラミング競技プログラミング

E - Complete Compress

公式解説とちょっと違う方法で通したので書いておきます。

解法

木DPを考える

コマを集める頂点を全て試すことにします。集める頂点を $r$ と表記し、 $r$ を根とする木DPを考えます。

それぞれの頂点 $i$ について、それ以下にある部分木に含まれるコマは必ず頂点 $i$ を通ります。そこで「ある頂点 $i$ 以下の部分木にあるコマを全て頂点 $i$ に集めるために、部分木の外にあるコマと行う操作の回数」を考え、これを単に「外との操作回数」と呼ぶことにします。問題の条件を満たす動かし方は、根について外との操作回数が0回になるような動かし方と言うことができます。

そこで各頂点について以下のような値を計算する木DPを考えてみましょう。

$dp\lbrack i \rbrack =$ 頂点 $i$ 以下の部分木にあるコマを全て頂点 $i$ に集めるために、部分木の外にあるコマとの操作を最小で何回行う必要があるか。

つまり外との操作回数の最小値です。これが $dp\lbrack r \rbrack = 0$ となれば目的達成です。

遷移を考える

次にこのDPの遷移を考えましょう。

ある頂点 $j$ について $dp\lbrack j \rbrack$ が求められているとします。それらのコマを親 $i$ に動かすためには、それぞれのコマについてさらに1回ずつの操作が必要になります。つまり頂点 $j$ 以下の部分木に含まれるコマの個数を $n\lbrack j \rbrack$ として $dp\lbrack j \rbrack + n\lbrack j \rbrack$ 回の操作が必要です。

頂点 $i$ について外との操作回数を最小にするためには、それぞれの子について必要な操作回数を集めて、違う子同士で可能な限り相殺して…と考えたいところですが、それぞれの部分木で可能な限り相殺して外との操作回数を小さくしてしまうと後で困るケースがあります。例えば以下のようなケースです。

f:id:betrue12:20190605015220p:plain

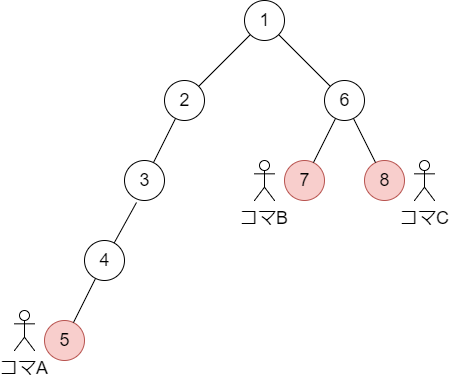
このケースは頂点1に全コマを集めることが可能ですが、貪欲に相殺して頂点6を見る段階でコマBとCを操作してしまうとアウトです。正解はコマAとBの操作、コマAとCの操作を2回ずつ行うことです。

このようなケースはどのように考慮するべきでしょうか。愚直解法としては、最小値だけでなく外との操作回数として取りうる値を全て持っておく…というものが考えられますが、実は取りうる値の最小値と最大値を持っておくことで解決します。この最大値は「部分木で一切の相殺をしない」という場合に相当するので、すなわち部分木内の各コマと頂点 $i$ との距離の和になります。

このことについて細かく見ていき、遷移を詰めていきましょう。

遷移を細かく考察する

まず、頂点 $i$ それぞれについて外との操作回数は必ず偶数・奇数どちらかになります。これは外との操作回数が、その最大値から部分木内だけで操作された回数の2倍を引いたものであることから分かります。

そして操作回数の最小値と最大値の間にある値は、偶奇が一致していれば必ずそれらの値を実現する操作が可能です。これは最小値を実現する操作から、部分木内で行っている操作を1組ずつ解消していくと考えれば良いです。

この性質を利用してDPの遷移を考えましょう。頂点 $i$ についての外との操作回数の最小値と最大値を子たちの情報から求めます。最大値は先述の通り各コマと頂点 $i$ との距離和として単純に計算できるので、考えるべきは最小値です。

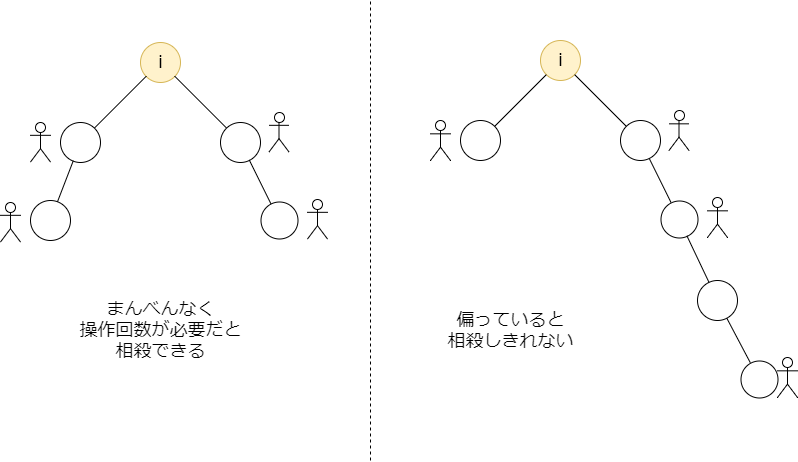
子が1つしかないときは相殺できないので明らかです。複数の子がある場合、イメージとしては必要操作回数がまんべんなく散らばっていると相殺できて最小値は小さくできます。逆に1つの子だけに操作回数が偏っていると相殺しきれない分が増えます。

f:id:betrue12:20190605020233p:plain

これを具体的に式で書いていきましょう。子 $j$ についての外との操作回数の最大値を $dp_{\max}\lbrack j \rbrack$ とし、先程まで $dp\lbrack j \rbrack$ としていた最小値を改めて $dp_{\min}\lbrack j \rbrack$ とします。先程と同じく頂点 $j$ 以下の部分木に含まれるコマの個数を $n\lbrack j \rbrack$ とします。

頂点 $i$ の子全ての集合を $J$ とします。このとき、 $dp_{\min}\lbrack i \rbrack$ は以下のように計算することができます。

$\displaystyle dp_{\min}\lbrack i \rbrack = \max_{k\in J}\lbrace (dp_{\min}\lbrack k \rbrack + n\lbrack k \rbrack) - \sum_{j\in J, j\ne k} (dp_{\max}\lbrack j \rbrack + n\lbrack j \rbrack) \rbrace$

※ただしこの値が負になる場合は、偶数なら0、奇数なら1。

つまり $k$ が「操作回数を相殺しきれないかもしれない子」の候補で、これを全部試します。 $k$ の操作回数を最小に、他の子の操作回数を最大にしたときに、相殺しきれないぶんがあればそれは頂点 $i$ のさらに外との操作で補わないといけません。これを全ての $k$ について試した最大値が $dp_{\min}\lbrack i \rbrack$ となります。

もちろん負にはなれないのでそこは考慮します。計算結果が負になったときに偶数なら0、奇数なら1を実現する操作が必ず存在することは、それぞれの子について先程の「操作回数の最小値の最大値の間にある値は、偶奇が一致していれば必ずそれらの値を実現する操作が可能」という性質が成り立っていることから言えます。

これで遷移ができました。先程の $\displaystyle dp_{\min}\lbrack i \rbrack$ の計算は、 $\sum_{j\in J, j\ne k}$ の部分については全部の合計を計算しておいて1個引けばよいので、子の個数についての線形時間で計算できます。つまり木DPが全体で $O(N)$ になり、根を全部試しても全体 $O(N^{2})$ で間に合います。

付録：逆走について

これは公式解説でも触れられていますが、コマを集める頂点 $r$ を決めた時に、その頂点から一方のコマが遠ざかるような操作（逆走）はしても得がないことは確かめておく必要があります。ここまでの解法では逆走については一切考慮していませんでした。

f:id:betrue12:20190605020451p:plain

不必要に逆走すると操作回数は増えるので明らかに損です。もし仮に「逆走なしで考えると不可能だけど、あえて逆走することで条件を満たす操作が可能になる」という可能性があれば逆走を考慮する必要がありますが、そのようなこともありません。それを（厳密ではないですが）軽く説明します。

もし頂点 $i$ のある子 $j$ について、 $j$ 以下の部分木の中で逆走をしてみたとします。このときその2つのコマは、片方は頂点 $i$ から遠ざかり片方は近づくので、 $i$ との距離和は変化しません。つまり部分木の外と行う必要がある操作回数も同じです。そのためもし逆走を含む操作で条件を満たせるならば、外との操作を行うコマを適切に入れ替えることで逆走なしで条件を満たせるはずです。

このことから、あえて逆走することに得はないことが分かります。

ACコード

Submission #5762278 - AtCoder Grand Contest 034

説明とコードの相違点として、DPの遷移計算で親に持っていく時に $n\lbrack j \rbrack$ を足すところを予め子側のdfs関数の最後で足しているので、読む際はそこを注意してください。

2019-05-28

Codeforces Round #556 B. Three Religions

Codeforces プログラミング競技プログラミング

お題箱より。

Problem - B - Codeforces

問題概要

英小文字からなる長さ $n$ の文字列 $S$ が与えられる。また文字列 $T_{1}, T_{2}, T_{3}$ があり、これらは最初は空である。

以下のクエリが合計で $q$ 個与えられる。

1 i c 文字列 $T_{i}$ の末尾に文字 $c$ を足す。
2 i 文字列 $T_{i}$ の末尾の文字を取り去る。

各クエリに対して、そのクエリを処理した後の $T_{1}, T_{2}, T_{3}$ に対する以下の問いに答えよ。

$S$ の文字を色1、色2、色3、無色に塗り分け、色 $i$ に塗られた文字を順に読むと $T_{i}$ に一致するようにできるか？

制約

$1 \le n \le 100000$
$1 \le q \le 1000$
文字列 $S$ および1クエリで与えられる文字は全て英小文字である
空文字列に対して2クエリが与えられることはない
全ての時点で $T_{1}, T_{2}, T_{3}$ はいずれも250文字を超えない

解法

問題1回の解き方を考える

まずはクエリのことを忘れて、1回問題を解くことを考えましょう。

文字列を左から見ていくことで、例えばこんなDPが考えられます。

$dp\lbrack i \rbrack\lbrack a \rbrack\lbrack b \rbrack\lbrack c \rbrack =$ 文字列 $S$ の最初の $i$ 文字目まで見たときに、 $T_{1}, T_{2}, T_{3}$ のそれぞれ $a, b, c$ 文字目までが塗られているようにできるか？（true/false）

これでは状態数が多いですね。ここで「できる/できない」などのブール値を値とするDPは、その添字のうちの1つを値にしてしまうことで状態数を削減できる可能性があります。例えば、

$dp\lbrack a \rbrack\lbrack b \rbrack\lbrack c \rbrack =$ $T_{1}, T_{2}, T_{3}$ のそれぞれ $a, b, c$ 文字目までが塗られているようにするためには、最小で文字列 $S$ の最初の $i$ 文字目までを見ればよいか？（ただし、不可能な場合はINFとする）
$dp\lbrack i \rbrack\lbrack a \rbrack\lbrack b \rbrack =$ 文字列 $S$ の最初の $i$ 文字目まで見て、 $T_{1}, T_{2}$ はそれぞれ $a, b$ 文字目まで塗られているときに、 $T_{3}$ は最大で何文字まで塗られているようにできるか？

のような変形が考えられます。このように添字の1つを「最小の○○」「最大の○○」のように値のほうに持ってくることで状態数を削減できます。今回の場合は $a, b, c$ の値がそれぞれ250以下であることから、上のほうを採用したいです。

あとはちゃんと遷移を計算できるようにします。例えば $dp\lbrack a \rbrack\lbrack b \rbrack\lbrack c \rbrack = x$ のとき、 $dp\lbrack a+1 \rbrack\lbrack b \rbrack\lbrack c \rbrack$ は何になるでしょうか？それは「 $T_{1}$ の $a+1$ 文字目と同じ文字が、 $S$ の $x$ 文字目より後ろで一番近くにあるところ」となります。

これは事前に「 $S$ の $i$ 文字目より後ろで、文字 $k$ が一番近くにあるのはどこか？」という情報を全ての $(i, k)$ に対して計算しておけばすぐに求められます。これは後ろから見ていくことで全て求められて、文字は26種類なので十分間に合います。

$T_{1}, T_{2}, T_{3}$ の長さをそれぞれ $A, B, C$ として、 $dp\lbrack A \rbrack\lbrack B \rbrack\lbrack C \rbrack$ がINFでなければ答えはYesです。ということで、判定を1回するだけなら解けそうです。

クエリへの対応を考える

クエリのたびにさっきのDPをやり直していては間に合いません。クエリでは $T_{1}, T_{2}, T_{3}$ どれかの末尾が1文字増減するだけなので、ほとんどの結果は使い回せるはずです。

クエリが来る前の $T_{1}, T_{2}, T_{3}$ の長さをそれぞれ $A, B, C$ としましょう。そして、この時点で $dp\lbrack a \rbrack\lbrack b \rbrack\lbrack c \rbrack$ の値が $0 \le a \le A, 0 \le b \le B, 0 \le c \le C$ に対して既に求まっているとしましょう。ここにクエリが来た時の処理を考えます。

クエリ2の場合

文字を削除するクエリの場合は簡単です。例えば 2 1 というクエリが来ると $T_{1}$ の長さは $A-1$ になります。このとき $dp\lbrack A-1 \rbrack\lbrack B \rbrack\lbrack C \rbrack$ の結果はそのまま使うことができます。この値がINFでなければYesです。

クエリ1の場合

文字を追加するクエリの場合は、新しく計算をするべき部分が出てきます。ただ使い回せる部分は使いましょう。

例えば 1 1 <何か> というクエリが来ると $T_{1}$ の長さは $A+1$ になります。このときは $dp\lbrack A+1 \rbrack\lbrack b \rbrack\lbrack c \rbrack$ を新しく計算する必要があります。

この更新部分は $b, c$ が最大でそれぞれ0～250まで動き得るので $251^{2}$ 箇所で、1つに対する遷移は高々3通りです。新しく更新する場所についてループを回したほうが分かりやすいので、実装は貰うDPがオススメです。

これを計算した後に $dp\lbrack A+1 \rbrack\lbrack B \rbrack\lbrack C \rbrack$ がINFでなければYesです。クエリ数が1000以下なので、ちょっと厳しいですが何とか間に合います。

ACコード

Submission #53529480 - Codeforces

2019-05-26

AtCoder Beginner Contest 127 F - Absolute Minima

AtCoder プログラミング競技プログラミング

F - Absolute Minima

解法

最適な $x$ の条件

定数項 $b$ については単に答えに足すだけなので、 $a$ についてだけ考えます。

更新クエリをいくつか処理した後の式

$f(x) = |x-a_{1}| + |x-a_{2}| + \cdots + |x-a_{k}|$

を最小にするような $x$ の値は、 $a_{1}, ..., a_{k}$ の中央値になります。これは以前の記事に説明を書いているのでそちらも参考にしてください。

そのため、この問題は

クエリで動的に値を追加しながら、以下の値を求める。
- $a_{i}$ の中央値を効率的に求める。
- $x$ をその中央値としたときの $f(x)$ を効率的に求める。

という処理ができれば解けることになります。

ここで、問題文の「最小値を実現する $x$ が複数存在するときには最小の $x$ を答える」という要求に注意しておきましょう。要素が奇数個の場合は中央値が厳密に1つなのでこの値を答えれば良いですが、偶数個の場合は中央にある2要素の間ならどこを取っても $f(x)$ が最小になるので、その2要素のうち小さい方を答える必要があります。要素数を $k$ として、（1-indexedで）小さい方から $\lceil \frac{k}{2}\rceil$ 番目の要素、ということになります。

中央値の求め方

値を動的に追加/削除しながらその中央値を求める方法はいくつかありますが、私はBIT（Binary Indexed Tree）を使いました。

BITは数列のある1点に値を加算することと、範囲和を求めることができるデータ構造です。これを中央値を求めるために使うことができます。

先ほど見たように今回求めたい中央値は小さい方から $\lceil \frac{k}{2}\rceil$ 番目の値であり、つまり「 $m$ 以下の要素が $\lceil \frac{k}{2}\rceil$ 個存在する」という条件を満たす最小の $m$ ということになります。

つまり値 $a_{i}$ の追加を「BITのインデックス $a_{i}$ に1を加算する」と処理しておけば、中央値は範囲和を用いて二分探索をすることで求めることができます。

最小値の求め方

次に実際の $f(x)$ の値です。これもいちいち計算していると間に合いません。

中央値 $m$ が求められたとすると、そこを境に絶対値の符号が逆転します。つまり $a_{i} \lt m$ のものについては $|m-a_{i}| = m-a_{i}$ となり、 $a_{i} \gt m$ のものについては $|m-a_{i}| = a_{i}-m$ となります。

つまりそれぞれの領域ごとに、その総和はある範囲での $a_{i}$ の総和と $m \times (その範囲にある a_{i} の個数)$ から求めることができます。ある範囲に存在する $a_{i}$ の個数は先ほどのBITで求められ、その総和についても「値 $a_{i}$ を追加したときに、BITのインデックス $a_{i}$ に $a_{i}$ を加算する」というBITを別途用意しておけば求められます。

座標圧縮を忘れずに

この解法で解く場合、 $a_{i}$ の値をBITのインデックスにする必要があるので $-10^{9} \le a_{i} \le 10^{9}$ という制約の大きさがネックになります。これは予め座標圧縮をしておくことで対応することができます。

ACコード

Submission #5607909 - AtCoder Beginner Contest 127

2019-05-26

AtCoder Beginner Contest 127 E - Cell Distance

AtCoder プログラミング競技プログラミング

E - Cell Distance

解法

この問題は結構考察ステップが多いです。順番に考えていきましょう。

数え上げの順番を変える

まず考えることは「数え上げの順番を変える」ことです。抽象的な書き方ですが、これが具体的にどういうことか説明します。

問題文では以下のことが問われていますね。

駒の全ての配置に対して以下を求め、合計する。
- その配置における駒2つのペア全通りを考えて、そのマンハッタン距離を合計したもの。

処理イメージとしては以下のような感じです。（文法とかはあまり深く気にしないでください）

for(haichi in all_haichi){
    for(pair in all_pairs(haichi)){
        ans += kyori(pair);
    }
}

これはとても考えにくいです。というのも、ループの外側で回っている通り数が膨大にあるからです。

ということで考え方を変えましょう。for文の順番を逆にします。

マス2つのペア全通りに対して、以下を合計する。
- そのマスに駒が置いてあるような駒の配置の通り数と、マス間のマンハッタン距離の積。

処理イメージはこんな感じになります。

for(pair in all_possible_pairs){
    haichi_num = calc_num_of_haichi(pair);
    ans += kyori(pair) * haichi_num;
}

これだと多少は考えやすくなります。マスの数を $A = NM$ と置くと、マス2つのペアとしてあり得るのは $\frac{A(A-1)}{2}$ 通りです。これでもまだ間に合いませんが、先ほどと比べると何とかなりそうに思えます。

ここで「あるマス2つに駒が置いてあるような駒の配置の通り数」を計算してみましょう。これはその2マスがどこであっても、残りのマス $A-2$ 個に残りの駒 $K-2$ 個を置く場合の数になります。そのため通り数は $_{A-2}C_{K-2}$ となります。（問題文の最後に書いてあるように、駒同士は区別しないことに注意してください）

そのため結局求める値は、

マス2つのペア全通りについてそのマンハッタン距離を合計して、最後に $_{A-2}C_{K-2}$ を掛けたもの。

として求めることができます。かなり見通しが良くなりました。

縦横の分離

次に考えるべきは縦横の分離です。求めたいのはマンハッタン距離の総和であり、縦の距離と横の距離を別々に計算して足しても同じ結果が得られます。

以降は縦の距離だけについて考えていきます。横の距離は以降の計算を、 $N$ と $M$ を入れ替えて行えばよいです。

距離を固定して計算

ここからの計算量削減の考え方はいくつかありますが、公式解説に準拠しましょう。

2マス間の縦の距離を、ある値 $d$ に固定します。距離0は計算に入れなくて良いので $1 \le d \le N-1$ とします。そして、「縦の距離が $d$ になるようなペアの通り数」を求めます。

このとき以下の図のように、2つの縦座標の選び方は $N-d$ 通りあります。そしてそれぞれに対して横座標が $M$ 通りあるので、ペアの通り数は $(N-d)M^{2}$ あります。

f:id:betrue12:20190526155257p:plain

つまり「マス2つのペア全通りについてマンハッタン距離（の縦だけ）を合計した値」は

$\displaystyle \sum_{d=1}^{N-1} d(N-d)M^{2}$

で求められることが分かります。

あとはこれを横についても求めて足し、最後に $_{A-2}C_{K-2}$ を掛ければ答えになります。

ACコード

Submission #5627987 - AtCoder Beginner Contest 127

さいごに

ここまで見てきたように、この問題は考察ステップが多く難しめです。しかしこの「数え上げの順番を変える」というテクニックは、数え上げ問題を攻略していく上では欠かせない超重要テクニックになります。

イメージとしては「for文の順番を入れ替える」、もしくは「縦に見るものを横に見る」というのも良い表現だと思います。この感覚を身に着けて、直接数えにくいなと思ったときに「順番を入れ替えたら楽になったり、二項係数などでまとめて計算できないだろうか？」と目を付けることができたら、難しめの数え上げ問題でも糸口が掴めるようになります。

その意味でも、新ABCとしてとても良い問題だったんじゃないかなと個人的には思います。

2019-05-26

Codeforces Round #561 F. Vicky's Delivery Service

Codeforces プログラミング競技プログラミング

お題箱より。

Problem - F - Codeforces

問題概要

$n$ 頂点 $m$ 辺の無向グラフがあり、各辺は $c$ 色のうちどれかの色で塗られている。

以下のクエリを $q$ 個処理せよ。

+ x y z 頂点 $x, y$ 間に色 $z$ の辺を追加する。
? x y 頂点から頂点までの、以下の条件を満たすパスが存在するかどうか答える。
- 始点から1本目と2本目の辺の色が同じ、3本目と4本目の辺の色が同じ...というように、2本ずつ同じ色の辺を通る。（ただしパス長が奇数である場合、最後の辺には条件がない）

制約

$1 \le n \le 10^{5}$
$1 \le m, c, q \le 10^{5}$
$1 \le x, y \le n$
$1 \le z \le c$
全ての時点において、自己ループと多重辺は存在しないことが保証される

解法

メインの考え方

まず奇数長のパスは考えないことにしましょう。偶数長であり、ある頂点 $i$ から2本ずつ同じ色の辺を渡るパスを「良いパス」と呼ぶことにします。

ある頂点 $i$ から良いパスによって到達できる頂点たちを考えます。するとこれらの頂点たちの中からどの2頂点を選んでも、その間は良いパスで互いに到達できるはずです。これらの頂点を $x, y$ として、 $i$ との良いパスを繋げた $x\to i \to y$ というパスはやはり良いパスになっているからです。

そのため、この「良いパスによって互いに到達可能な頂点の集合」をUnion-Findで管理することができます。

まず最初の時点でのグラフについて、この集合はどのように求めることができるでしょうか？効率の良い方法は「長さ2の良いパスの、真ん中に注目する」ことです。ある頂点（図中の仲介役）から同じ色の辺が2本出ていれば、その相手同士は長さ2の良いパスで互いに到達可能ということになります。

このとき全てのペアを連結しようとする必要はなく、図のように併合をしていけば併合回数はおよそ辺の数の2倍で抑えることができます。

f:id:betrue12:20190525235821p:plain

まずはこの処理を、全ての点を仲介役として回します。これで最初の時点での集合が作れます。

1クエリの処理

次にこのグラフに 1 x y z クエリで辺を追加する方法を考えます。その場合も先程と同じように、頂点 $x, y$ それぞれについて、その頂点を仲介役と見たときにどの頂点同士が良いパスで到達可能になるかを考えればよいです。

f:id:betrue12:20190526000103p:plain

2クエリの処理

最後に 2 x y クエリ、ここで奇数長のパスを考え始めましょう。問題の条件を満たすパスは「良いパス」または「良いパスの最後に1回の移動をしたもの」になります。前者は同じ集合に入っているか調べればいいので簡単ですが、後者が厄介ですね。

併合した集合それぞれに対して、「含まれる頂点のどこかから移動1回で到達できる頂点の集合」を管理することにしましょう。説明のため「隣接点集合」という名前を付けておきます。

そうすると、「良いパスの最後に1回の移動をしたもの」によって始点から終点に移動できる条件は、始点が含まれる集合の隣接点集合に終点が入っていることです。この集合を管理できていれば答えがすぐに求められそうです。

隣接点集合の初期値としては単純に各頂点の隣接点を入れておけば良いです。頂点集合をマージしたときに、それらの隣接点集合もマージする必要があります。これはいわゆる「データ構造をマージする一般的なテク」により、要素数の小さいほうから大きい方にマージすることで計算量を抑えることができます。

1クエリで辺が増えたときには、こちらの隣接点集合にも追加する必要があることに気をつけてください。

これで全ての処理を扱う方法を揃えることができたので、問題を解くことができます。

ACコード

Submission #54314619 - Codeforces

説明と少し違う点として、隣接点集合に各頂点自身も含むようにしています。こうすると先程の「良いパス」と「良いパスの最後に1回の移動をしたもの」の両方を隣接点集合を見ることでチェックできるので少し楽です。

解法

Aさんの行動

Bさんの行動

ACコード

解法

連結成分に閉路がない場合

連結成分に閉路がある場合

ACコード

解法

木DPを考える

遷移を考える

遷移を細かく考察する

付録：逆走について

ACコード

問題概要

制約

解法

問題1回の解き方を考える

クエリへの対応を考える

クエリ2の場合

クエリ1の場合

ACコード

解法

最適な の条件

中央値の求め方

最小値の求め方

座標圧縮を忘れずに

ACコード

解法

数え上げの順番を変える

縦横の分離

距離を固定して計算

ACコード

さいごに

問題概要

制約

解法

メインの考え方

1クエリの処理

2クエリの処理

ACコード

最適な $x$ の条件