ARMERIA

Rubyと競技プログラミングの話　AtCoderやCodeforcesの問題解説記事が多め。

AtCoder Regular Contest 061 E - すぬけ君の地下鉄旅行

AtCoder プログラミング 競技プログラミング

お題箱より。

E - すぬけ君の地下鉄旅行 / Snuke's Subway Trip

解法

グラフの最短路問題として解けそうではありますが、異なる運営会社間での乗り換えを考慮する必要があります。つまり「どの駅にいるか」だけでなく、「その駅でどの会社の路線に乗っているか」という情報が必要になります。

このようなときに、「駅 i にいて会社 j の路線に乗っている」という状態をペア (i, j) として、このペアそれぞれを1つの頂点としてグラフを作るテクニックがあります。こうすれば電車での駅間の移動や乗り換えのコストを正しく扱うことができます。同じ駅かつ違う会社の頂点に乗り換えるときにコスト1が掛かると思えばよいです。

f:id:betrue12:20190525122446p:plain

このように状態を組み合わせるときは頂点の個数がものすごく大きな数にならないか気を付ける必要がありますが、今回は2駅間を繋ぐ路線が M 個与えられることから、この頂点数は最大でも全部で 2M 個です。

ただしこの方針で全ての乗り換えパターンに辺を張ってしまうと、大量の路線が乗り入れる駅があったときに辺数がものすごい数になってしまいます。

f:id:betrue12:20190525123812p:plain

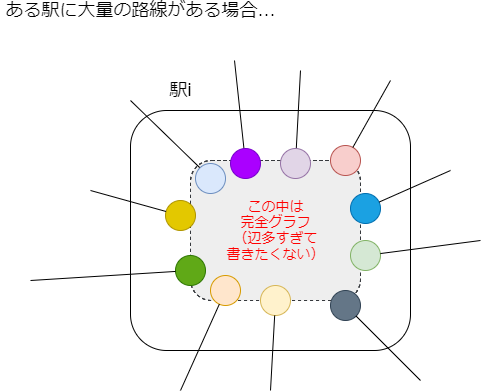
これは困るのでもう少し工夫しましょう。乗り換えを、「改札を出る」動きと「次の路線の改札に入る」動きに分類します。そして「改札の外」を表す頂点をさらに追加します。

f:id:betrue12:20190525134259p:plain

このようにすると、辺数が頂点数の2倍で抑えられます。今までは無向グラフとして扱えていましたが、この時点でグラフが有向グラフになっていることに注意してください。

あとはこのグラフ上でダイクストラ法などを回せば答えを求めることができます。辺のコストが0または1なので01-BFSでも良いですね。

ACコード

Submission #5571322 - AtCoder Regular Contest 061

（リクエストくれた人の言語が分からなかったのでC++にしています…RubyかPythonなら書けるので必要なら言ってください）

実装に関してですが、駅番号と会社番号（「改札の外」の場合は-1としています）のペアを頂点として扱う必要があります。しかもこれらの頂点の距離などを2次元配列などで管理すると、スカスカでサイズの大きな配列が必要になってしまいます。

実装方針は色々あると思いますが、いったん使う頂点をペアとして列挙し、重複を排除した後に「座標圧縮」の要領でペアに番号を振ってしまうのが分かりやすいと思います。ここでペアから頂点番号を逆引きできるmapなども作っておくと楽です。

新しく振った番号で辺を全て張り直してしまえばあとはこっちのものです、普通にダイクストラ法や01-BFSをすればよいです。上記リンク先のコードでは01-BFSにしています。

いろはちゃんコンテスト Day2 H - 根室の巫女

AtCoder プログラミング 競技プログラミング

お題箱より。

H - 根室の巫女

解法

Morris-Pratt法について

まず、公式解説（？）にも書いてあるMorris-Pratt法（MP）について触れておきます。私も実戦で使ったことはないのですが…ある長さ N の文字列 S があったときに、全ての i=1, ..., N に対して以下の値を求めた数列 B_{1}, ..., B_{N} を求めるアルゴリズムです。

  • S の先頭 i 文字だけからなる文字列を s_{i} とする。 i 未満の整数 k であって、「 s_{i} の先頭 k 文字と末尾 k 文字が一致する。」という条件を満たす k の最大値を B_{i} とする。

k=i としてしまうと先頭 k 文字と末尾 k 文字は当然一致してしまうので、それ以外で最大のものを求めることに注意してください。

この数列は文字列検索を高速に行う際などに使うようです。丁寧な解説と具体的な実装は以下のブログ記事が分かりやすいです。

※今回の「Morris-Pratt法とは何か」という説明は、上記記事に準じて書いています。Morris-Pratt法で調べると「上記の数列を活用して文字列検索を行うこと」をMorris-Pratt法と呼んでいたり、色々違ったことが書いていて私もよく分かりません…。

さて、上記の数列の定義はそのまま今回の問題で与えられる B_{1}, ..., B_{N} の定義になっています。文字列から数列を求めるMP法とは逆に、この問題ではこのような数列を満たす元の文字列（数列ですが）を構成することになります。

解き方について

さて解き方ですが…公式解説（？）はよく分からないので、私が解いた（コンテスト後にTwitterで見た）解法ベースで書きたいと思います。

以降、数列 A_{1}, ..., A_{N} を単に A 、数列 B_{1}, ..., B_{N} を単に B と表記します。

最初にこの解法の大まかな流れを書いておきます。

  1. B として与えられた条件を満たすような解 A が存在すると仮定し、その必要条件を用いて数列 A を構成する。
  2. 構成した数列 A に対してMorris-Pratt法を適用し、本当に条件を満たしているかを判定する。

必要条件を考える

まず条件を満たすような解 A が存在すると仮定して、 A が満たすべき必要条件を考えます。具体的には B の「最大の」という条件を考えないことにすると、以下の必要条件が得られます。

  • A の先頭 i 要素だけからなる配列を a_{i} とする。 a_{i} の先頭 B_{i} 要素と末尾 B_{i} 要素は一致する。

これを元に、「同じ値である必要がある要素」をまとめていくことを考えましょう。例えば各インデックスを頂点とみなして、Union-Findを用いて以下のように辺を張れば、どの要素の値が同じ必要があるかを管理できます。

f:id:betrue12:20190525102625p:plain

ただしこの辺は合計で \sum B_{i} 本あり、全て処理していると計算が間に合いません。

繋ぐべき辺を削減する

繋ぐ辺を削減しましょう。実は、「各 i に対して、上記の両文字列の末尾だけを繋ぐ」という処理だけで、結果的にこれら全てのペアが同じ連結成分に属してくれることを示すことができます。その理由を説明します。

端的に言うと、「末尾以外のところは他のインデックスが繋いでくれる」というのが理由になっています。例えば1つ前のインデックス j=i-1 について考えると、これがちゃんとインデックス B_{i}-1 と連結になって欲しいです。

ここで少なくとも以下の図の赤いところについては値が一致していることから、必ず B_{j} \ge B_{i}-1 が成立します。

f:id:betrue12:20190525104055p:plain

これがもし B_{j} = B_{i}-1 だった場合は簡単で、インデックス j に対して「末尾同士を繋ぐ」という処理をしたときにインデックス B_{i}-1 と繋がれます。

もし B_{j} \gt B_{i}-1 だった場合、直接繋がれることはありません。ですがこの場合、以下の図のようになっているはずです。

f:id:betrue12:20190525104911p:plain

図中の赤いところは全て一致しているので、そのインデックスを辿っていくことで必ず B_{i}-1 文字目に辿り着きます。つまりこれらの辺を張っていくことで同じ連結成分に属するようにできます。

このように考えると、「各インデックスに対して一致してほしい部分数列の末尾同士を繋ぐ」という操作を全てのインデックスにすることで、末尾以外についても一致してほしいところは最終的に同じ連結成分に属してくれることが分かります。

数字を割り当てる

…というわけで、必要条件から「一致してほしいインデックス」が連結成分として求められました。これらに対して適当に数字を割り振っていきましょう。

このとき、違う連結成分なのに同じ数を割り当てることにメリットはありません。何故なら先ほどの必要条件は B について「最大の」という条件を考えないようにしたものであり、より長い長さで a_{i} の先頭と末尾が一致してしまうとアウトです。つまり「これ以上はなるべく一致してほしくない」わけです。それなら違う連結成分には違う数字を割り当てるほうが良いですね。

Moris-Pratt法で検証する

これで解の「候補」ができました。これまで見てきたように、作ってきた数列は必要条件を満たし、かつ十分性を最も満たしやすいように作ったものです。

これをMoris-Pratt法で検証し、得られた数列が B と一致していればそれが答えです。一致しなかった場合は解がないと判定して良いです。

ACコード

Submission #5567680 - いろはちゃんコンテスト Day2

AtCoder Beginner Contest 126 F - XOR Matching

AtCoder プログラミング 競技プログラミング

F - XOR Matching

解法

結論を書いてしまうと、以下のような数列がもし作れれば答えになります。

f:id:betrue12:20190520210750p:plain

アイデアとしては、まず K を挟んで K 以外の数字を鏡写しに並べます。こうすることで K 以外のどの数字を選んでも、2つの位置の間（両端を含む）にあるものは「 K 1個と、同じ数字の2個ペアたち」となり、同じ数字のペアはXORで打ち消し合うので必ずXORの値が K になります。

あとは K 同士のXORも K にならないといけませんが… M \ge 2 の場合は もう1つの K を端に置くことで間にある値のXORが必ず K になります。これは、

  • a を非負整数として、 4a, 4a+1, 4a+2, 4a+3 のXORを取ると必ず0になる

という性質によるものです。この性質は以前のABCにも登場しましたね。

M \ge 2 であれば 0, 1, ..., 2^{M}-1 は上記のような4つ組のグループに分けられるので、そのXORは0になります。今回 K と K の間（両端を含む）にある値はこれらの値1つずつと K 1個だけが余っているので、そのXORは K になります。

ということで、 K \le 2^{M}-1 かつ M \ge 2 のときは答えを求めることができました。あとは残りのケースを考慮します。

もし K \ge 2^{M} である場合には、 K の最上位ビットは 2^{M} の位以上になり、 0, 1, ..., 2^{M}-1 の値をどうXORで組み合わせてもこのビットを作ることはできません。つまり、この場合は構成不可能です。

M = 1 の場合は入出力例に示されている通りなので、これをそのまま埋め込んでしまえばよいです。 M = 0 も実は制約に含まれていますが、この場合は 0 0 しか作れないので K=0 の場合だけ答えが存在します（考慮していなくても M \ge 2 と同じ実装で正しく処理できることが多いでしょう）。

ACコード

Submission #5462845 - AtCoder Beginner Contest 126

Codeforces Round #561 D. Cute Sequences

Codeforces プログラミング 競技プログラミング

Problem - D - Codeforces

問題概要

以下の問題を q 個解け。

  • 正整数 a, b, m が与えられる。以下の条件を満たす整数列 \lbrace x_{i} \rbrace を1つ構成するか、そのような数列が存在しないことを判定せよ。
    • 初項が a で末項が b である。
    • 項数を n として、全ての 2 \le i \le n について r_{i} = x_{i} - \sum_{k=1}^{i-1}x_{k} とすると 1 \le r_{i} \le m が成立する。

制約

  • 1 \le q \le 10^{3}
  • 1 \le a \le b \le 10^{14}
  • 1 \le m \le 10^{14}

解法

数列の長さ n を全探索することを考えましょう。 n = 1 のときに条件を満たすのは a=b の時だけなので、その場合は別扱いすることにして n \ge 2 の場合を考えます。

長さ n をある値に固定して、末項が最小でどのくらいの値になるか考えます。すなわち全て r_{i} = 1 としたときの末項を計算してみます。

  • x_{1} = a
  • x_{2} = x_{1} + 1 = a+1
  • x_{3} = x_{1} + x_{2} + 1 = 2a+2
  • ...
  • x_{n} = x_{1} + \cdots + x_{n-1} + 1 = 2^{n-2}(a+1)

実際に計算してみるとこのような値になります。もしこの値が既に b よりも大きい場合は、これ以上の長さでは絶対に答えを構成できないことが分かります。

2^{n-2}(a+1) \le b のときは、ここから各 r_{i} を増やすことで b との差を埋めることを考えます。各 r_{i} を1増やしたときに、末項の値はどれだけ増えるでしょうか。これも実際に手計算すると分かって、

  • i \lt n のとき、 r_{i} が1増えると末項は 2^{n-1-i} だけ増える。
  • r_{n} が1増えると末項は1だけ増える。

というようになります。

最小値の時点で既に1持っているので、各 r_{i} について増やせるのは m-1 までです。これらの値をうまく決めて、先ほどの係数を掛けた合計が増やすべき値 d = b - 2^{n-2}(a+1) に一致するようにすればよいです。これは係数が大きい方から決めていって、足りない分を増やせるだけ増やすようにすることで求めることができます。

この方針で決めていっても合計が増やすべき値 d に満たない場合は、その数列の長さで条件を満たすものは存在しないことになります。これを 2^{n-2}(a+1) \le b となるような n 全てについて計算し、条件を満たすものが見つからなかったら答えは存在しないと判定することができます。

2以上の長さの候補はおよそ \log_{2} \frac{b}{a+1} 個なので、クエリが最大 10^{3} 個あることを加味しても計算時間は問題ないです。

ACコード

Submission #54298174 - Codeforces

コード中で L という変数でループを回していますが、 L = n-2 として扱っているので読む場合はご注意ください…

Educational Codeforces Round 65 E. Range Deleting

Codeforces プログラミング 競技プログラミング

Problem - E - Codeforces

問題概要

長さ n の数列 \lbrace a_{i} \rbrace と整数 x が与えられ、 1 \le a_{i} \le x である。

以下の条件を満たす整数の組 (l, r) の個数を求めよ。

  • 1 \le l \le r \le x である。
  • 数列 \lbrace a_{i} \rbrace から l \le a_{i} \le r を満たす要素をすべて取り除くと、残った数列は広義単調増加になる。（空数列でも可）

制約

  • 1 \le n, x \le 10^{6}
  • 1 \le a_{i} \le x

解説

削除する値の範囲 \lbrack l, r \rbrack について、ある左端 l を固定したとき、条件を満たす r には単調性があります。これは区間を伸ばせば伸ばすほど多くの要素が消え、残った数列が単調増加になりやすいからです。

二分探索かしゃくとり法が使えないか考えてみましょう。二分探索ができれば楽ですが、 x 個の左端を全探索した上で判定問題を解くのに n 要素の数列を走査しているようでは間に合いません。しゃくとり法を用いて、かつ区間に値を出し入れする処理を何らかの方法で差分更新できれば間に合いそうです。

この差分更新は様々な方法で実現している人がいました。この記事では私が本番中に実装したやり方をまとめておきます。

ある要素 a_{i} に注目します。数列を左から右に並べたときに、もしこの要素より左にあって a_{i} より大きい要素があると数列は単調増加になりません。そのため条件を満たすためには、インデックス i に関して

  1. a_{i} が削除される。
  2. i より左にあって a_{i} より大きい要素の最小値を m_{i}、最大値を M_{i} として、範囲 \lbrack m_{i}, M_{i} \rbrack が全て削除される。

の少なくとも一方が満たされる必要があります。ただし i より左に a_{i} より大きい要素が存在しないような i については常に条件が満たされていると考えてよいです。

f:id:betrue12:20190516222708p:plain

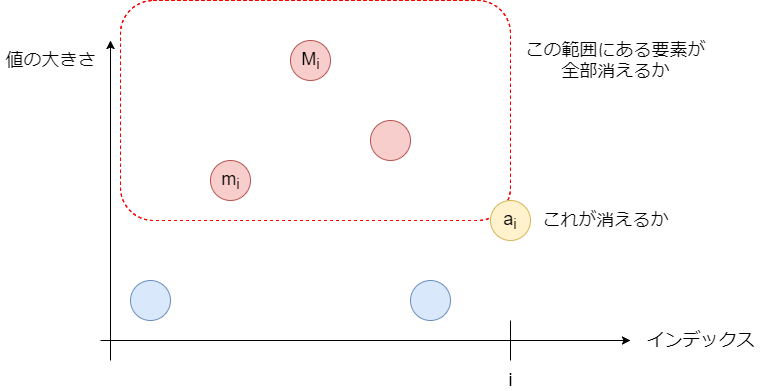
逆に全ての i についてこれらの条件の少なくとも一方が満たされるとき、数列は単調増加になります。

そこでまず、それぞれの i について m_{i}, M_{i} を求めます。これは数列を左から見ていきながらsetやセグメント木に値を追加していくことで合計 O(N \log N) で実現できます。

そしてしゃくとり法を以下のように処理していきます。

  • 区間の右端に値 v を加えるときには、
    • a_{i} = v である i について、条件1を「満たす」に変更する。
    • M_{i} = v である i について、もし l \le m_{i} ならば条件2を「満たす」に変更する。
  • 区間の左端から値 v を取り除くときには、
    • a_{i} = v である i について、条件1を「満たさない」に変更する。
    • m_{i} = v である i について、もし M_{i} \le r ならば条件2を「満たさない」に変更する。
  • 上記の変更に伴って、「今、条件がどちらも満たされていないインデックス i の個数」を差分更新する。

このようにすれば、区間に値を出し入れして差分更新する処理は合計で O(N+X) になります。合計で O(N\log N+X) となり、制約が大きいのでギリギリですが一応間に合いました。

ACコード

Submission #54241812 - Codeforces

Codeforces Round #560 F2. Microtransactions (hard version)

プログラミング 競技プログラミング Codeforces

Problem - F2 - Codeforces

問題概要

※microtransactionは、オンラインゲームなどでのアイテム課金を指す言葉だそうです。文中では「アイテム」と訳します。

イヴァンはゲームのアイテムを買おうとしている。アイテムは n 種類あり、種類 i のアイテムは k_{i} 個必要である。

イヴァンは毎日の朝に1円を稼ぎ、夜にアイテムを買う。アイテムは通常1個2円だが、「 d_{j} 日目には、種類 t_{j} のアイテムを1円で買える」というセール情報が合計で m 個与えられる。

イヴァンは所持金が足りる限り1日にアイテムを好きなだけ買うことができる。イヴァンが全てのアイテムを必要数買い終わるまでの最小日数を求めよ。

制約

  • 1 \le n, m \le 2 \times 10^{5}
  • 0 \le k_{i} \le 2 \times 10^{5}
  • 1 \le \sum k_{i} \le 2 \times 10^{5}
  • 1 \le d_{j} \le 2 \times 10^{5}
  • 1 \le t_{j} \le n

解法

この問題は、アイテムを全て買い終わる日を決めてしまうととても考えやすくなります。「アイテムを X 日までに買い終わることは可能か？」という判定問題を考えて二分探索します。

アイテムの値段は全て同じなので、セールで買うアイテムの合計個数を最大化することを目指せばよいです。そしてアイテムは各日に好きなだけ買うことが可能なので、セールでの買い物は出来るだけ先延ばししたほうが使えるお金が多いので有利です。

そのため最適な戦略は

  • 各アイテム種類ごとに、 X 日までの間で一番最後のセール日しか買わないようにする。各アイテムごとに最後のセール日をリストアップしておく。
  • 前からシミュレートする。基本はお金を貯めて、リストアップしたセール日が来たらそのアイテムを買えるだけ買う。
  • 最終日に、セールで買えなかった不足分をまとめ買いする。

となります。買い終わる日を決めることで一番最後のセール日がいつなのかが分かり、最適な戦略が決まります。

二分探索の初期条件について考えましょう。 S = \sum k_{i} とします。アイテムの合計必要個数×2のお金があればセールなしで全部買えるので ok = 2S とできます。一方、全部セールで買ったとしても間に合わない条件を考えると ng = S - 1 とできます（適当に ng = 0 などでも問題ないです）。

二分探索のループが O(\log S) 回実行され、それぞれの判定問題は実装によりますが O(N+M) で可能なので、全体計算量は O((N+M)\log S) となり間に合います。判定問題は各アイテムごとの最後のセール日を調べた後にソート等をするともう1つ \log が付きますが、日数が少ないことを利用してバケットで管理すると線形時間になります。

ACコード

Submission #54115676 - Codeforces

少し前に二分探索の記事を書いたばかりだったので、タイムリーでした。