ARMERIA

Rubyと競技プログラミングの話　AtCoderやCodeforcesの問題解説記事が多め。

Codeforces Round #604 (Div. 1) C. Beautiful Mirrors with queries

Codeforces プログラミング競技プログラミング

お題箱より。

Problem - C - Codeforces

私のコンテスト中の思考をベースに書きます。ちょっとややこしいかも。

問題概要

$n$ 個の門があり、これを門 $1$ から門 $n$ まで順番に突破していく。スタート地点は門 $1$ の直前であり、門 $n$ を突破すればクリアである。

門 $i$ の突破に挑戦すると、確率 $\frac{p_{i}}{100}$ で突破できる。もし突破できなかった場合、「チェックポイント」として指定された門のうち、番号が $i$ 以下で最も大きいものの直前に戻される。

最初の状態では門 $1$ のみがチェックポイントである。以下のクエリを $q$ 個処理せよ。

$2$ 以上の門の番号 $u$ が与えられるので、門 $u$ がチェックポイントかどうかを反転させる。その後、クリアまでの合計挑戦回数の期待値（有理数）を $\bmod 998244353$ で答えよ。

制約

$2 \le n, q \le 2\times 10^{5}$

解法

いちいち $100$ で割るのが面倒なので門の突破確率を単に $p_{i}$ を表記することにします。具体的には入力に予め $100^{-1}$ を掛けておきます。

あるチェックポイントの直前から、次のチェックポイントの直前までを1つのセットと考えることができます。仮想的にクリア状態もセットの終端と思うことにすると、スタートからクリアまでは独立なセットに分割できます。これらのセットそれぞれを突破するための挑戦回数の期待値をすべて足したものがクエリの答えです。

1つのセットを突破するための挑戦回数の期待値を求めましょう。簡単のため、スタート地点である門 $1$ の直前からスタートし、次のチェックポイントが門 $4$ だとします。

f:id:betrue12:20191210213638p:plain

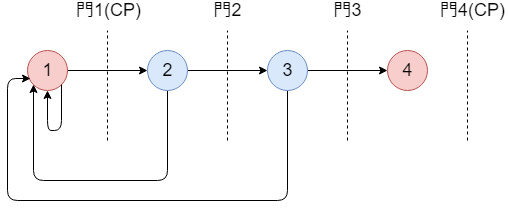
上図において門 $1$ の直前からスタートして、「門 $4$ の直前に到達する」か「門 $1$ の直前に戻ってくる」かどちらかに至るまでの経路は以下の4種類です。

経路	確率	使った挑戦回数
門 $1$ で失敗する。	$P_{1} = 1-p_{1}$	1
門 $2$ で失敗する。	$P_{2} = p_{1}(1-p_{2})$	2
門 $3$ で失敗する。	$P_{3} = p_{1}p_{2}(1-p_{3})$	3
門 $3$ まで突破する。	$P_{4} = p_{1}p_{2}p_{3}$	3

このことから、門1の直前から門4の直前に到達するまでの挑戦回数の期待値を $E$ とすると、以下が成り立ちます。

$E = (1 + E)P_{1} + (2 + E)P_{2} + (3 + E)P_{3} + 3P_{4}$

$E$ を含む項を全て左辺に移項します。 $P_{1} + P_{2} + P_{3} + P_{4} = 1$ であることから以下のように式変形できます。

$P_{4}E = 1P_{1} + 2P_{2} + 3P_{3} + 3P_{4}$

左辺は良いとして、右辺の計算は各 $P$ が面倒な値なので難しそうです。しかしこれを以下のように理解してみましょう。

f:id:betrue12:20191210215927p:plain

この図のように考えると、実は先ほどの右辺は $1 + p_{1} + p_{1}p_{2}$ と書けて、結局 $E$ は

$\displaystyle E = \frac{1 + p_{1} + p_{1}p_{2}}{p_{1}p_{2}p_{3}}$

と求められることになります。

つまり $E$ を求めるにあたっては、 $p_{i}$ の累積積（？）と、その累積積についてさらに累積和を取ったものを前計算しておけば高速に計算できそうです。これらをそれぞれ以下のように表記します。

$M_{i} = p_{1}p_{2}\cdots p_{i}$ 、ただし $M_{0} = 1$
$S_{i} = M_{0} + \cdots + M_{i-1}$ 、ただし $S_{0} = 0$

一般の場合を考えると、1セットにおけるスタート地点は門 $1$ の前とは限りません。例えば門 $s, t$ がチェックポイントで、間に他のチェックポイントはなく、門 $s$ の直前から門 $t$ の直前までのセットを突破するための挑戦回数の期待値を $E$ とすると

$\displaystyle E = \frac{1 + p_{s} + p_{s}p_{s+1} + \cdots + (p_{s}\cdots p_{t-2})}{p_{s}\cdots p_{t-1}}$

という値になります。このように途中から始まる場合でも、この値は門 $1$ から計算した $M_{i}, S_{i}$ を用いて求めることが可能です。具体的には以下のようになります。

$\displaystyle E = \frac{S_{t-1} - S_{s-1}}{M_{t-1}}$

これで、どの門と門の間が1セットになっても、そのセットを突破するための挑戦回数の期待値は $O(1)$ で求められるようになりました。

あとはクエリの処理です。ある1つの門が新しくチェックポイントになった場合、既存の1セットが2つのセットに分割されるので、消えるセット区間と増えるセット区間それぞれについて期待値を求めて答えから足し引きすればOKです。1つの門がチェックポイントでなくなる場合はその逆です。

このセット区間が具体的にどこかを知るには、操作される門の左右それぞれで一番近いチェックポイントがどこか分かれば良くて、これは遅延セグ木やBIT二分探索などを用いるとクエリあたり $O(\log n)$ で求めることができます。

これで問題を解く全ての材料が揃いました。私の解法の全体計算量は（逆元計算を定数時間とすれば） $O(n + q\log n)$ になりました。

ACコード

Submission #66350491 - Codeforces