お題箱より。
解法
グループを作れる条件がなかなか扱いづらいことや制約の小ささからDPの線を考えます。
上手くDPを組むコツは「覚えておくべき情報を減らす」、逆に言うと「状態を忘れられるようにする」ことです。例えばこの問題において、「 人組を作って、
人組を作って、また
人組を作って…」という風に無秩序にグループを決めていくような考え方をすると、「これまで○人組を△つ作った」という情報を全部覚えておかなければいけません。
一方、「 のとき
人組の個数と
人組の個数には関係がない」という点に注目すると、「
人組のグループを一気に全て決めてしまう」という処理を
について順番に行っていく…という考え方ができます。このとき覚えておくべき情報は「既に作られたグループで何人使ったか」だけです。それぞれの人についてグループを組める条件が違ったりはしないので、誰が使われたかの情報も必要なくて人数だけで十分です。
ということで、以下のようなDPテーブルを定義します。
：
人組のグループを全て決めてしまって、
人が使われているような場合の数
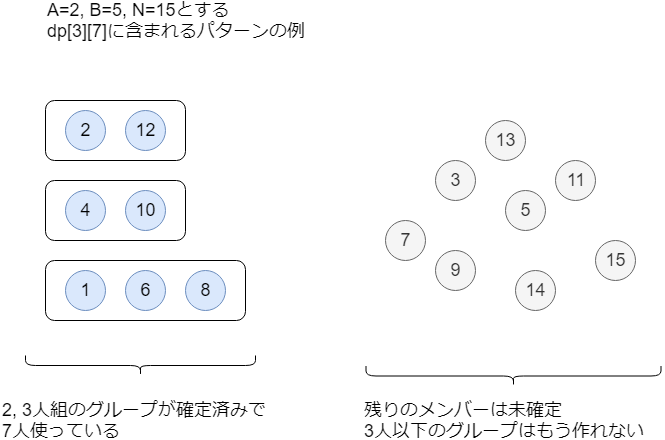
例えば として、
というのは以下のような状態を指しています。
遷移を考えましょう。 からの遷移係数は、残っている
人から
人組をいくつか組む通り数になります。
人組を
個作るとすると、
に遷移するときの係数は
という値になります。その内訳は
：
人残っている中で使う
人を選ぶ
：
人を選ぶという処理を
回繰り返す
：グループの区別をしないので
で割る
というものです。
このとき の値と
として取り得る値の最大値は反比例のようになっています。このことから調和級数の性質を用いて計算量が
と評価できます。遷移のたびに
を毎回計算しているとけっこう時間がかかるので注意です。