JOI春合宿2015 K - 遺産相続
お題箱より。JOIの解説記事は初めてかな…?
解説途中の証明についてのリクエストだったのでそこを重点的に書きます。
解法
最大全域木として考える
都市を「頂点」、鉄道を「辺」、鉄道の収益を「辺重み」と考えます。
「閉路ができない範囲で取れるだけ取る」という処理は最小(最大)全域木のアルゴリズムで実現できます。まず子供1の辺の取り方は、
- 辺を重みが大きい方から順に見ていく。
- それぞれの辺について、それを追加することで閉路ができないならば、その辺を取る。
というクラスカル法のアルゴリズムで求めることができます。重みが相異なるという条件から、この取り方は一意です。
子供2以降は、自分より前の子供が誰も使わなかった辺だけについて同じことを繰り返します。閉路ができるかの判定のためには、各子供がそれぞれグラフ(実装上はUnion-Find木だけで十分)を持って連結状態を管理しておけば良いです。
これを最後の子供までやれば答えが求められる…のですが、辺が大量に後ろまで残るようなケースだと、単純計算で(子供の人数)×(辺の数)×(追加できるかの判定の計算量)くらいの計算量がかかることになります。
処理順序の逆転
発想を逆転させて、辺を重み順に見ていくというループを外側に持ってきます。つまり、
- 子供を番号順に見ていく。
- 残っている辺を重み順に見ていき、取れる(閉路ができない)ならば取る。
ではなく、
- 辺を重み順に見ていく。
- それを取れる子供のうち、最も番号の小さい子供がその辺を取る。
という処理をします。
これを単純にやると計算量はさっきと同じです。ですがこの「辺を取れる子供のうち、最も番号の小さい子供」を効率的に求める方法が存在します。
何となくの考察としては、番号の小さい子供のほうが優先的に辺を取るので、頂点同士が連結になっている度合いが高いです。であればある頂点 間を結ぶ辺を追加するときに、「
が既に連結である子供」と「
がまだ連結でない子供」はある番号を境にキレイに分かれているのでは、と推測できます。この単調性が成り立っていれば二分探索ができます。
この証明を考えます。公式解説は帰納法として書いていますが、背理法っぽく書きます。本質的にはだいたい同じだと思います。
単調性の証明
上記の性質が成り立たない、つまり
処理の途中で、ある頂点の組 について、ある子供
では非連結で、それより番号の大きいある子供
について既に連結である状態になっている
と仮定します。このとき子供 のグラフにおいて頂点
間を結ぶパスが存在します。説明を簡単にするため、例えば中継する頂点を
の2個として、3辺
がグラフに含まれているとします。
一方、子供 より番号の小さい子供
の持つグラフでは
が非連結なので、
のうち少なくともどれか1組は非連結です。であれば、子供
が持っている3辺のうちどれか1つは子供
に取られているはずです。これは矛盾です。
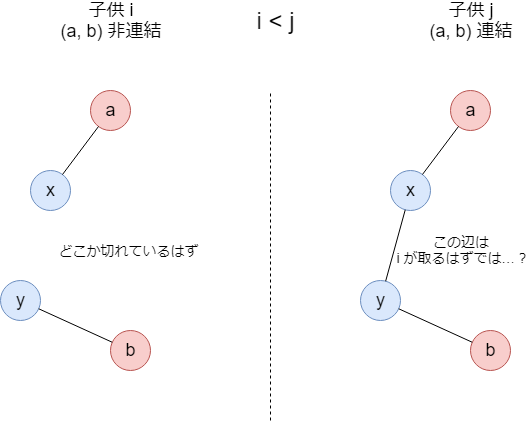
実際には中継する頂点がいくつであっても同じ証明ができます。よって背理法から先ほどの単調性は必ず成り立つことが分かります。
これで二分探索ができるので間に合います。C/C++しか使えないJOI春合宿での問題なのでちょっとタイトですね。