2020-10-20

AtCoder Grand Contest 048 D - Pocky Game

AtCoder プログラミング競技プログラミング

D - Pocky Game

解法

各山の石の個数について、その初期値を $A_{i}$ と表し、ゲームの途中経過における値を $a_{i}$ と表すことにします。

まずは全ての状態を網羅するDPを

もし石の総数が十分少なければ、以下のDPで全ての局面の勝敗状態を求めることができます。

$dp_{1}\lbrack l\rbrack\lbrack r\rbrack\lbrack a_{l}\rbrack\lbrack a_{r}\rbrack$ ：「先手の手番で、1個以上の石が残っている山の番号が $l$ から $r$ までで、山 $l$ の石の個数が $a_{l}$ 、山 $r$ の石の個数が $a_{r}$ である」という状態が先手勝ちであればtrue、後手勝ちであればfalse。
$dp_{2}\lbrack l\rbrack\lbrack r\rbrack\lbrack a_{l}\rbrack\lbrack a_{r}\rbrack$ ：「後手の手番で、1個以上の石が残っている山の番号が $l$ から $r$ までで、山 $l$ の石の個数が $a_{l}$ 、山 $r$ の石の個数が $a_{r}$ である」という状態が後手勝ちであればtrue、先手勝ちであればfalse。

当然ながらこれでは状態数が多すぎるので減らす方法を考えます。

単調性に気付く

1個以上の石が残っている山の番号が $l$ から $r$ までである状態をまとめて考えます。このとき、先手は自分が操作する山 $l$ に残っている石 $a_{l}$ が多いほど有利です（それ以外の状況が全く同じである場合）。同様に後手は山 $r$ に残っている石 $a_{r}$ が多いほど有利です。石が多い状態からは、余分に石を取ることで石が少ない状態と同じ遷移ができるからです。

この性質を利用すると、自分側の石の個数をキーではなく値の方に持つ、以下のようなDPの状態を考えることができます。

$dp_{1}\lbrack l\rbrack\lbrack r\rbrack\lbrack a_{r}\rbrack$ ：先手の手番で、1個以上の石が残っている山の番号が $l$ から $r$ までで、山 $r$ の石の個数が $a_{r}$ であるとき、山 $l$ の石の個数がこの値以上であれば先手勝ち、そうでなければ後手勝ちである。
$dp_{2}\lbrack l\rbrack\lbrack r\rbrack\lbrack a_{l}\rbrack$ ：後手の手番で、1個以上の石が残っている山の番号が $l$ から $r$ までで、山 $l$ の石の個数が $a_{l}$ であるとき、山 $r$ の石の個数がこの値以上であれば後手勝ち、そうでなければ先手勝ちである。

これは「bool値を持つDPで、あるキーについて単調性がある場合、そのキーを値にすることで状態数を減らせる」という汎用性の高いテクニックです。ですがこれでもまだ間に合わないのでさらに状態を削ります。

「山の石を取り切った瞬間」だけを考える

1ターンずつ全ての状態を考えていると間に合わないので、ゲームにおいて区切りとなるような状態だけ考えて、それらの勝敗判定ができないか考えます。

ゲームの流れを大雑把に区切ると、「いずれかのプレイヤーが自分側の山の石を全て取り切る」というイベントが合計 $N$ 回起こります。このように相手が山の石を全て取り切って自分にターンが回ってきた瞬間には、相手側の次の山には石が全て残っています（石が残っている山が1個以下になる場合を除く）。このような状態だけをピックアップします。

$dp_{1}\lbrack l\rbrack\lbrack r\rbrack$ ：先手の手番で、1個以上の石が残っている山の番号が $l$ から $r$ までで、山 $r$ の石の個数が初期値 $A_{r}$ のままであるとき、山 $l$ の石の個数がこの値以上であれば先手勝ち、そうでなければ後手勝ちである。
$dp_{2}\lbrack l\rbrack\lbrack r\rbrack$ ：後手の手番で、1個以上の石が残っている山の番号が $l$ から $r$ までで、山 $l$ の石の個数が初期値 $A_{l}$ のままであるとき、山 $r$ の石の個数がこの値以上であれば後手勝ち、そうでなければ先手勝ちである。

ただし石が残っている山が1個である場合は個数に関わらず石を全部取り切って勝てるので、全ての $i$ について $dp_{1}\lbrack i\rbrack\lbrack i\rbrack = dp_{2}\lbrack i\rbrack\lbrack i\rbrack = 1$ とします。これがDPの初期状態です。

これでようやく状態数が $O(N^{2})$ になります。ですが1手ずつの状態を考えていないので、遷移を求めるのに工夫が必要です。

遷移計算

$dp_{1}\lbrack l\rbrack\lbrack r\rbrack$ の求め方を考えます。もう片方も同様です。

まず、それぞれのプレイヤーが取る行動としては「1個だけ取る」「山の石を全部取る」の2通りだけ考えれば十分であることが分かります。他の条件が同じであれば自分側の山の石が多いほうが有利なので、取り切らないのに2個以上取るという行動は自分を不利にするだけだからです。

もしいきなり先手が全取りして勝ち状態に持っていける場合は、 $dp_{1}\lbrack l\rbrack\lbrack r\rbrack = 1$ です。こうなる条件は、全取りすることで後手に渡す状態が後手にとって負け状態であること。つまり $dp_{2}\lbrack l+1\rbrack\lbrack r\rbrack \gt A_{r}$ であることです。

そうでない場合、先手が1個取り、後手が1個取り…という行動を繰り返してそれぞれの石が減っていき、「ここで全取りすれば勝ち」という状態に先になったほうが勝ちます。先手側の山 $l$ にある石の個数を $x$ とすると、こうなるまでの行動回数は

先手が全取りで勝てるようになるまでに必要な後手の行動回数： $a_{r}=A_{r}$ から始まって $dp_{2}\lbrack l+1\rbrack\lbrack r\rbrack \gt a_{r}$ を満たす状態まで減って欲しいので、 $A_{r}-dp_{2}\lbrack l+1\rbrack\lbrack r\rbrack+1$ 回必要。
後手が全取りで勝てるようになるまでに必要な先手の行動回数： $a_{l}=x$ から始まって $dp_{1}\lbrack l\rbrack\lbrack r-1\rbrack \gt a_{l}$ を満たす状態まで減って欲しいので、 $x-dp_{1}\lbrack l\rbrack\lbrack r-1\rbrack+1$ 回必要。

と計算することができます。先手の手番であることを考慮すると、先手が勝てる条件は

$A_{r}-dp_{2}\lbrack l+1\rbrack\lbrack r\rbrack+1 \lt x-dp_{1}\lbrack l\rbrack\lbrack r-1\rbrack+1$

なので、 $x$ が整数であることを考慮してこれを解くと

$x \ge dp_{1}\lbrack l\rbrack\lbrack r-1\rbrack + A_{r}-dp_{2}\lbrack l+1\rbrack\lbrack r\rbrack+1$

となります。

よって整理すると、 $dp_{1}\lbrack l\rbrack\lbrack r\rbrack$ は以下のように求められます。

$dp_{2}\lbrack l+1\rbrack\lbrack r\rbrack \gt A_{r}$ である場合、 $1$
そうでない場合、 $dp_{1}\lbrack l\rbrack\lbrack r-1\rbrack + A_{r}-dp_{2}\lbrack l+1\rbrack\lbrack r\rbrack+1$

これで遷移が計算できるので、区間が狭い方から順番に求めていきます。最終的に先手が勝つ条件は $A_{1} \ge dp_{1}\lbrack 1\rbrack\lbrack N\rbrack$ で判定することができます。

ACコード

Submission #17514189 - AtCoder Grand Contest 048

2020-10-05

個数制限付き部分和問題+条件を満たす選び方の数え上げ

AtCoder プログラミング競技プログラミング

先日のコンテストの問題における、最後の高速化について知りたいというリクエストがあったため、解説を書きます。より一般的な「個数制限付き部分和問題+条件を満たす選び方の数え上げ」という枠組みで説明します。

扱う問題

正整数 $N, S$ と、正整数からなる長さ $N$ の数列 $\lbrace a_{0}, ..., a_{N-1}\rbrace, \lbrace b_{0}, ..., b_{N-1}\rbrace$ が与えられる。

$a_{0}$ を $0$ 個以上 $b_{0}$ 個以下、 $a_{1}$ を $0$ 個以上 $b_{1}$ 個以下…と選ぶ方法のうち、その総和が $S$ であるような方法の個数を $10^{9}+7$ で割った余りを求めよ。

より形式的には、以下の条件を満たす非負整数列 $\lbrace n_{0}, ..., n_{N-1}\rbrace$ の個数を $10^{9}+7$ で割った余りを求めよ。

全ての $i$ に対して $0 \le n_{i} \le b_{i}$
$\sum_{i}n_{i}a_{i} = S$

この問題を全体計算量 $O(NS)$ で解きます。

解法

普通の部分和問題と同様にDPをします。状態を以下のように定義します。

$dp\lbrack i\rbrack\lbrack j\rbrack$ ： $a_{0}, ..., a_{i-1}$ をそれぞれいくつ使うか決めて、それまでの総和が $j$ であるような場合の数

このDPテーブルのサイズは $(N+1)(S+1)$ です。

$a_{i}$ をいくつ使うかを決める時の遷移を、貰うDPで考えます。 $dp\lbrack i+1\rbrack\lbrack j\rbrack$ に遷移するのは、

$dp\lbrack i\rbrack\lbrack j\rbrack$ から、 $a_{i}$ を $0$ 個使うことにして遷移
$dp\lbrack i\rbrack\lbrack j-a_{i}\rbrack$ から、 $a_{i}$ を $1$ 個使うことにして遷移
…
$dp\lbrack i\rbrack\lbrack j-b_{i}a_{i}\rbrack$ から、 $a_{i}$ を $b_{i}$ 個使うことにして遷移

という $b_{i}+1$ 個の遷移元のうち、添字が非負であるものです。

これらを全て個別に遷移していては最悪ケースで $O(NS^{2})$ 掛かってしまうので、以下のいずれかの手法で高速化します。

高速化手法1：累積和

先ほどの説明から、DPの遷移式は以下のようになります。

$dp\lbrack i+1\rbrack\lbrack j\rbrack = dp\lbrack i\rbrack\lbrack j\rbrack + dp\lbrack i\rbrack\lbrack j-a_{i}\rbrack + \cdots + dp\lbrack i\rbrack\lbrack j-b_{i}a_{i}\rbrack$

$j$ を $j \bmod a_{i}$ が等しいグループに分けて、グループごとに $dp\lbrack i\rbrack\lbrack j\rbrack$ の累積和を取っておきます。そうするとこの右辺は1つのグループ内での区間和になるので、累積和から $O(1)$ で計算できます。これで全体計算量 $O(NS)$ を達成できます。

高速化手法2：差分更新

本質的には高速化手法1とほぼ同じですが、より実装が楽だと思います。

$dp\lbrack i+1\rbrack\lbrack j\rbrack$ と $dp\lbrack i+1\rbrack\lbrack j-a_{i}\rbrack$ の遷移元がほとんど同じで1つだけずれていることを利用すると、 $j$ を小さい方から求めていきながら以下の式で差分更新することができます。

$dp\lbrack i+1\rbrack\lbrack j\rbrack = dp\lbrack i+1\rbrack\lbrack j-a_{i}\rbrack + dp\lbrack i\rbrack\lbrack j\rbrack - dp\lbrack i\rbrack\lbrack j-(b_{i}+1)a_{i}\rbrack$

添字が負である領域の値は全て $0$ とします。この計算は $O(1)$ でできるので、同様に全体計算量 $O(NS)$ を達成できます。

f:id:betrue12:20201005120022p:plain

実装例

高速化手法2を使っています。

#include <bits/stdc++.h>
using namespace std;

int64_t MOD = 1e9+7;
void add(int64_t& a, int64_t b){
    a = (a+b) % MOD;
}
void mul(int64_t& a, int64_t b){
    a = a*b % MOD;
}

int main(){
    int N, S;
    vector<int> A(N), B(N);
    
    vector<vector<int64_t>> dp(N+1, vector<int64_t>(S+1));
    dp[0][0] = 1;
    for(int i=0; i<N; i++) for(int j=0; j<=S; j++) {
        dp[i+1][j] = dp[i][j];
        if(j-A[i] >= 0) add(dp[i+1][j], dp[i+1][j-A[i]]);
        if(j-(B[i]+1)*A[i] >= 0) add(dp[i+1][j], MOD-dp[i][j-(B[i]+1)*A[i]]);
    }
}

ACコード

冒頭にリンクを貼った問題のACコードリンクも貼っておきます。これが元のリクエストの回答になればと思います。

Submission #17202414 - AtCoder Regular Contest 104

2020-10-04

AtCoder Regular Contest 104 E - Random LIS

AtCoder プログラミング競技プログラミング

E - Random LIS

公式解説とは違う解法です（たぶん）。

解法

あり得る全ての場合に対するLISの長さを合計して、全事象数 $\prod A_{i}$ で割ることにします。

取っ掛かりが非常に掴みにくい問題ですが、 $1 \le N \le 6$ という制約から何らかの全探索をやることを目指してみます。

座標圧縮とゾーン分け

座標圧縮をします。数列 $A$ に含まれる値の種類数を $M$ として、 $A$ に $0$ を加えてソート・重複排除した数列を $p_{0}, p_{1}, ..., p_{M}$ （ $p_{0} = 0$ ）と置きます。するといずれかの $X_{i}$ が取り得る正整数の範囲は、 $(p_{0}, p_{1}\rbrack$ , $(p_{1}, p_{2}\rbrack$ , $(p_{M-1}, p_{M}\rbrack$ という半開区間で表される $M$ 個のゾーンに分けることができます。それぞれの $X_{i}$ は最大値 $A_{i}$ の値に応じて、このゾーンのうち前からいくつかに属することになります。

まず、 $X_{1}, ..., X_{N}$ がそれぞれどのゾーンに属するかを全探索します。これは $M^{N}$ 通りの全探索をすれば良いです。このとき $X_{i}$ がそのゾーンに属することができない（ $A_{i}$ が区間の下端以下である）ような $i$ がある場合、そのパターンは無視します。

ゾーン内部の大小関係

その上で各ゾーンについて、その内部での大小関係を全探索します。このとき複数の要素が同じ値を取り得る場合があるので、それも含めて全探索する必要があります。

ゾーンに含まれる要素の数が $n$ であるとき、数列 $\lbrace x_{0}, x_{1}, ..., x_{n-1}\rbrace$ の大小関係の列挙は、

長さ $n$ の非負数列で、その最大値が $m$ であるときに $0, 1, ..., m$ が全て含まれているもの

として列挙できます。この数列の個数が公式解説に書かれている Ordered Bell Numberです。例えば $n=4$ であって非負数列が $\lbrace 2, 0, 1, 0\rbrace$ であれば、大小関係は $x_{1}=x_{3} \lt x_{2} \lt x_{0}$ です。

この数列を予め要素数 $n=1, ..., N$ のそれぞれについて列挙しておくと、ゾーン分けを固定した後にそれぞれのゾーン内の大小関係を全探索できます。

場合の数とLISの長さ計算

ゾーン分けとゾーン内部の大小関係を全探索したら、そのパターンに該当する場合の数とLISの長さを計算して合計します。

場合の数は、各ゾーンで使う整数の選び方を計算した積になります。 $j$ 番目（0始まり）のゾーンに含まれる整数は $p_{j+1}-p_{j}$ 個であり、その中で $k$ 種類の整数を使う場合、その選び方は $_{p_{j+1}-p_{j}}C_{k}$ 通りです。

LISの長さは、ゾーン分けとゾーン内部の大小関係に応じて $X$ と大小関係が等しい数列を適当に作り、そのLISを求めれば良いです。例えば小さい方から $j$ 番目のゾーンで小さい方から $k$ 番目の値を $10j+k$ とすれば $X$ と大小関係が等しくなります。

計算量の評価は難しいですが、 $N=6$ で $A_{i}$ が全て異なる入力ケースにおいてパターン数を実際に計算すると $39208$ 通りでした。なのでこの中で毎回LISのアルゴリズムを回しても問題ないでしょう。

ACコード

Submission #17196593 - AtCoder Regular Contest 104

実装はなかなかの筋肉系です。

2020-09-28

Codeforces Round #673 (Div. 1) D. Graph and Queries

Codeforces プログラミング競技プログラミング

Problem - D - Codeforces

コンテスト中に自分が通した解法を書きます。

問題概要

$n$ 頂点 $m$ 辺の無向グラフが与えられ、頂点 $i$ には相異なる整数 $p_{i}$ が書かれている。

以下のクエリを合計 $q$ 個処理せよ。

1 v：頂点 $v$ と連結な頂点の中で最も大きい整数が書かれている頂点 $u$ を探し、 $p_{u}$ を出力する。その後、 $u$ に書かれている整数を $0$ に書き換える。
2 i：辺 $i$ を削除する。

制約

$1 \le n \le 2\times 10^{5}$
$1 \le m \le 3\times 10^{5}$
$1 \le q \le 5\times 10^{5}$

解法

辺を削除するクエリなので、逆から見ていけばUnion-Findが使えます。一方クエリ1に答えるためには「それ以前のクエリでどの整数が既に取られているか」の情報が必要なので、前から処理していく必要があります。

よって、辺が削除される過程を逆からUnion-Findで処理し、そのロールバックを行うことで前からクエリを処理できるようにするという方法を取ることにします。

Union-Findのロールバックは、経路圧縮を捨てればシンプルです。findクエリでは内部の状態は変化せず、unionクエリで変化する状態は定数個（親情報と、rankまたはsizeの情報）なので、「値を変更した配列のインデックスと変更前の値を時刻（クエリ番号）ごとに覚えておく」ことでロールバックが実現できます。

今回の問題の場合は追加で、各連結成分に含まれる $p_{i}$ の値の集合も持っておきたいです。これは set などで管理しておけば通称マージテクでマージすることができます。このとき「インデックス $i$ の set に値 $p$ を追加した」という情報を記憶しておけば、それを逆に削除することでロールバックできます。

ではこれを利用して前からクエリを処理していきましょう。クエリ2に対しては先ほど解説したロールバックをします。

クエリ1に対しては、その時点での頂点 $v$ のUnion-Findにおける根を求め、その根が持っている set を参照します。ただしこの set には以前のクエリで既に使われている整数が入っている可能性があるため、まず set の中の最大値が使用済みである限りその要素を取り除きます。その上で要素が残っていればその最大値がクエリの答えであり、要素が残っていなければ答えは $0$ です。

計算量としては、set の全要素数の合計がマージテクにより $O(n\log n)$ になるので、その挿入および削除の操作 $O(n(\log n)^{2})$ が一番重いです。経路圧縮を捨てるとUnion-Findの各クエリが $O(\log n)$ になるので、全体計算量としては $O(n(\log n)^{2} + (m+q)\log n)$ になります。

ACコード

（set 使用）Submission #94117179 - Codeforces

set の中で参照する値が最大値だけなので、削除処理を工夫すれば priority_queue でもできます。範囲for文が使えないのが地味に面倒だったりしますが…

（priority_queue 使用）Submission #94117213 - Codeforces

2020-09-27

第三回アルゴリズム実技検定 C - 等比数列

AtCoder プログラミング競技プログラミング

お題箱より。

C - Geometric Progression

解法というよりは「こういう問題を解くための思考プロセスが知りたい」というリクエストだったので、その方向で書きます。

解法

この問題は結局、等比数列の性質を知識として知っている、または実験によって理解することが重要です。なので正直なところ、「知らない場合は色々な値で実験しよう（またはWeb検索しよう）」というのが解くための近道だと思います。

初項 $A$ が正の数であるとき、等比数列は公比 $R$ の値に応じて以下のような挙動になります。

$R$ の範囲	挙動
$R \gt 1$	項が進むにつれて値が急速に大きくなる。
$R = 1$	全ての項が $A$ である。
$-1 \lt R \lt 1$	項が進むにつれて値が急速に $0$ に近付く。
$R = -1$	$A, -A$ を交互に繰り返す。
$R \lt -1$	正の数と負の数を交互に繰り返しながら、その絶対値が急速に大きくなる。

このように $R$ の値によって挙動が大きく変わるので、まずここで場合分けをする、という思考をします。今回の問題では $R$ が正の整数なので、最初の2項目だけを考えれば良いです。

次にそれぞれの場合について考えます。

$R \gt 1$ のとき

このときは値が急速に大きくなるため、少ない項数で $10^{9}$ を超えてしまうことが予想されます。それ以降は値が大きくなり続けるので、一度 $10^{9}$ を超えてしまうと答えは large で確定します。そのため「普通に等比数列の計算を順にしていって、 $10^{9}$ を超えたら large を出力して途中終了し、途中終了せずに第 $N$ 項まで計算できたらそれを出力する」という解法が考えられます。

large になるまで最大でいくつの項があるかを見積もります。 $A, R$ は正整数なのでできるだけ小さい方が値が小さくなりやすい（長引きやすい）です。今は $R \gt 1$ の場合を考えているので、その中で最小ケースである $A = 1, R = 2$ に対して実際に計算をすると第 $31$ 項で $10^{9}$ を超えることが分かります。

そのため $31$ 回以内の計算で「large になって途中終了する」または「第 $N$ 項が計算完了する」のどちらかによって答えが分かるので、実行制限時間に十分間に合います。

$R = 1$ のとき

全ての項が $A$ であり、 $A$ は $10^{9}$ 以下なので、 $A$ を出力すれば良いです。

まとめ

等比数列の性質に関しては、知識として覚えてしまうのが良いと思います。

また等比数列に限らず、「挙動が大きく変わるところで場合分けする」という思考プロセスが重要です。これは今回のようにある値を境界とした大小だったり、正負、偶奇、素数か合成数か…などなど色々あり得ます。思いつかなければ実験して探してみましょう。

そしてこのくらいの難度の問題であれば、その場合分け基準は数学的な基本知識や他の問題でも使える典型テクニックであることが多いので、1度出てきたものを覚えて次回使えるようにしておくのが重要だと思います。

ACコード

Submission #14064923 - 第三回アルゴリズム実技検定

2020-09-27

ACL Beginner Contest F - Heights and Pairs

AtCoder プログラミング競技プログラミング

F - Heights and Pairs

解法

まずは入力を各身長ごとの人数として集計します。 $a_{i}$ を身長が $i$ である人の人数とします。 $\sum_{i} a_{i} = 2N$ であり、 $0$ 人であるような身長を無視すれば身長の種類数は $2N$ 以下です。

条件を満たす組み方をDPなどで直接数えようとすると、 $O(N^{2})$ から落ちず厳しいです。

包除原理を適用します。同じ身長で組んでいるペアを「違反ペア」と呼ぶことにして、違反ペアを $0$ 個以上集めた集合を $s$ とします。「 $s$ に含まれるペアは必ず組んであって、その他のペアは自由に組まれているような組み方の数」を $C(s)$ とすると、答えは包除原理から

$\displaystyle \sum_{s} (-1)^{|s|}C(s)$

と計算できます。集合 $s$ の取り方は膨大にあるので $s$ のサイズごとに集計することにします。

まずはそれぞれの身長ごとに独立に、違反ペアをいくつか組む組み方を数えます。以下の値を計算します。

$c\lbrack i\rbrack\lbrack k\rbrack =$ 身長が $i$ の人の中で、違反ペアをちょうど $k$ 組だけ組むような組み方。（それ以外の人の組み方はまだ決めない）

これはまず、違反ペアに参加する人を選ぶのが $_{a_{i}}C_{2k}$ 通り。その中で違反ペアを組む組み方は、

まず $1$ 人適当に誰かを選び、その人の相方を残りの $2k-1$ 人の中から選ぶ。
また $1$ 人適当に誰かを選び、その人の相方を残りの $2k-3$ 人の中から選ぶ。
…

と考えると、二重階乗を用いて $(2k-1)!!$ 通りと計算できます。この $k$ は $0$ から $\lfloor\frac{a_{i}}{2}\rfloor$ まで取り得ます。

各身長ごとに求めた数列 $c\lbrack i\rbrack$ を全てマージします。身長 $1$ の人の違反ペアが $b_{1}$ 組、身長 $2$ の人の違反ペアが $b_{2}$ 組…という組み方を合わせると、合計違反ペアが $b_{1} + b_{2} + \cdots$ 組であるような組み方が $c\lbrack 1\rbrack\lbrack b_{1}\rbrack\times c\lbrack 2\rbrack\lbrack b_{2}\rbrack\times\cdots$ 通り得られます。これを全ての $(b_{1}, b_{2}, ...)$ について計算するので、これは数列をFFT（NTT）でマージすることに相当します。

これを最後までマージすると、以下の値を示す数列が得られます。

$c_{all}\lbrack k\rbrack =$ 全ての人の中で、違反ペアをちょうど $k$ 組だけ組むような組み方。（それ以外の人の組み方はまだ決めない）

これに残りのペアの組み方 $(2(N-k)-1)!!$ を掛けると、「 $|s| = k$ であるような $s$ についての $C(s)$ の和」が得られます。これを包除原理の式に従い合計すると答えになります。

あとはNTTのマージにかかる計算量を落とす必要があります。各身長に対する $c\lbrack i\rbrack$ の長さは $\lfloor\frac{a_{i}}{2}\rfloor + 1$ であり、 $\sum_{i} a_{i} = 2N$ なので、全ての数列の長さの和は $2N$ 以下です。

何も考えずにマージすると、長い数列に短い数列を何回もマージするような場合に最悪で $O(N^{2}\log N)$ の計算量が掛かってしまいます。

マージの順番を工夫して、以下の二分木のようにマージをするとどうでしょうか。

f:id:betrue12:20200927042025p:plain

二分木の1段分のマージでは、長さの和が $2N$ 以下である数列たちが1度ずつNTTでマージされるので、合計で計算量 $O(N\log N)$ になります。そして二分木のようにマージすると $O(\log N)$ 段で全てマージし終わるので、全体計算量 $O(N (\log N)^{2})$ でマージできます。

数列の本数が2冪でないときはトーナメントのシードのような扱いをします。また二分木でのマージとは挙動が少し異なりますが、数列たちをキューに入れて「先頭から $2$ 本取り出してマージした結果を末尾に入れる」という処理を $1$ 本になるまで繰り返しても同様の計算量が達成できます。

ACコード

Submission #17047575 - ACL Beginner Contest
（AtCoder Library使用）Submission #17058173 - ACL Beginner Contest

2020-09-27

ACL Beginner Contest E - Replace Digits

AtCoder プログラミング競技プログラミング

E - Replace Digits

先日、AtCoder Libraryの遅延伝播セグメント木の使い方について記事を書きました。

AtCoder LibraryのLazy Segtreeの使い方 - ARMERIA

今回の問題はセグ木にちょっと変なものを乗せる問題なので、上記の記事で解説していることの実践編として書いていこうと思います。この記事を読む前に上記の記事を読むことをオススメします。

解法

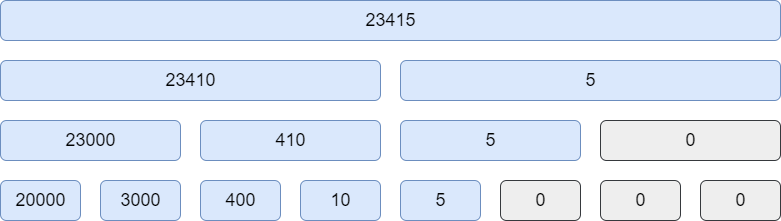
区間更新クエリと全体取得クエリを処理する問題です。遅延伝播セグメント木に乗せることを考え、まずは各ノードの data として何を持てば良いかを考えます。後で足りない情報があれば足すとして、まずは一番大事な「各桁の値」をどう持つか考えましょう。

これには何通りか方法があって、例えば $S$ 全体が $23415$ だったときに、末端のノードが持つ値を $\lbrace 2, 3, 4, 1, 5\rbrace$ と持つ方法や、 $\lbrace 20000, 3000, 400, 10, 5\rbrace$ と持つ方法があります。どちらでも解けますが今回は後者で考えてみます。

末端のノードが持つ値を $\lbrace 20000, 3000, 400, 10, 5\rbrace$ のようにすれば、区間同士をマージする二項演算 op は単なる足し算で良いです。この data だけを記したセグメント木の全体構造は以下のようになります。

f:id:betrue12:20200927012610p:plain

次に lazy として持つ「操作を表す値」を考えますが、これは更新クエリで書き換える1桁の整数をそのまま持てば良いでしょう。値を上書きする更新クエリなので、冒頭で紹介した記事の「区間更新操作の恒等写像」に書いたように恒等写像 id と操作同士をマージする関数 composition を定義します。

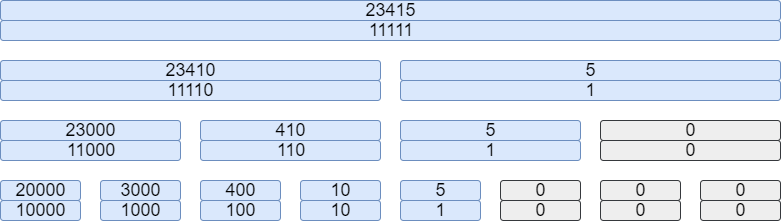
問題は操作を data に対して行う関数 mapping です。ある区間内の数字を一様に上書き更新したときに、その区間が受け持つ値が何になるべきかは区間によって異なります。例えば下図において赤色で塗っている区間 $\lbrack 0, 2)$ は万の位から千の位までの合計を担当しているので、「区間 $\lbrack 0, 2)$ の数字を一様に $d$ に変更する」という操作によってこのノードが持つデータは $11000\times d$ になるべきです。

f:id:betrue12:20200927014224p:plain

この $11000$ というのは、「そのノードが持つ区間内の数字を一様に更新したときに、その数字に対していくつの係数を掛ければその区間が受け持つ値の和になるか」という値です。これも一緒に data として持ってしまうことにしましょう。末端ノードについては右から $1, 10, 100, ...$ という値を持たせておいて、マージする関数 op においてこっちも単に足し算をしてあげれば良いです。各ノードが持つ data は以下のような構造になります。