2019-04-20

yukicoder No.819 Enjapma game

yukicoder プログラミング競技プログラミング

No.819 Enjapma game - yukicoder

writerさんの解法が天才なので、地道に実験して解いた私の解法もまとめてみたいと思います。

解法

「その盤面状態で自分のターンが回ってきた時に勝つ/負ける」という状態をそれぞれ勝ち状態/負け状態と呼ぶことにします。

駒の数が少ないほうから考えていきましょう。

駒が0個

操作できる駒がないので負け状態です。

駒が1個

その駒を取り除くことで駒0個の負け状態を相手に押し付けることができるので、これは勝ち状態です。

駒が2個

ここから少し考えることが増えます。

駒を取り除いてしまうと駒1個の勝ち状態を相手に与えてしまうので、2人は駒を動かすほうの操作をしたいです。いずれ動かせる駒が無くなって詰むわけですが、その盤面はどちらのプレイヤーが引いてしまうでしょうか。

駒の具体的な位置を考えてしまうと問題がとても複雑になるので、盤面を特徴づける何らかの便利な数を見つけたいです。このように「駒を隣に動かす」という操作をする問題の多くで有効なのが偶奇で、盤面を市松模様のように「左下からの距離が偶数か奇数か」で塗り分けます。そして「 $x$ 個の駒のうち $y$ 個が偶数マスにある」という状態を $(x, y)$ と特徴付けると、1つの駒を隣に動かす操作では $y$ の値が1増加または減少します。

f:id:betrue12:20190420134421p:plain

駒が2個の場合、動かせる駒がないときには必ず2つの駒は隣り合っているのでその偶奇は異なり、すなわちこれは $(2, 1)$ 状態です。そうすると、 $(2, 0), (2, 2)$ の盤面からは必ず相手に $(2, 1)$ の状態を押し付けることができて、 $(2, 1)$ 状態を押し付けられ続けて動かせる駒が無くなったプレイヤーが負けます。

駒が3個～4個

先ほど説明した状態 $(x, y)$ を利用して勝ち負けを考えていきます。ここで以下のような「パスカルの三角形」に似た図を用意します。

f:id:betrue12:20190420135038p:plain

この図において、プレイヤーの操作は

駒を取る：斜め上の状態を相手に与える。
駒を動かす：隣の状態を相手に与える。常に行えるとは限らない。

と考えることができます。

そうすると、この表の埋め方として

斜め上のどちらかに負け状態がある場合、それは勝ち状態である。
斜め上と隣が全て勝ち状態であることが確定している場合、それは負け状態である。

というルールを作ることができます。これで駒4個までの状態は埋まります。

f:id:betrue12:20190420135433p:plain

駒が5個～

駒が5個の場合を考えます。先ほどのルールで以下の図の状態までは埋まるのですが、両端はどうなるでしょうか。

f:id:betrue12:20190420135654p:plain

上側も内側も勝ち状態に囲まれているので、プレイヤーは可能な限りこの2マスを往復して押し付け合います。そのままいずれ駒が詰まった状態になって動かせなくなりますが…果たしてそのようなことはあるでしょうか？

ここで駒の偶奇の「偏り」に注目します。この図において両端に近いところは、駒が偶数マスと奇数マスの片方に極端に寄っていることを示しています。対して駒が詰まって動かせない状態というのは、直感的には偶数マスの駒と奇数マスの駒はだいたい同じくらいありそうです。

駒が詰まった状態で最大でいくつまで差が出る可能性があるか…というのを具体的に求める必要はありませんが、「駒の数が5個以上で、駒が詰まった状態で、偶数マスあるいは奇数マスの駒の個数が0～1個」という盤面は実際に並べてみるとあり得ないことが分かります。

ということは駒を取り除かずに動かし続ける限りは、必然的に内側のほうに遷移していくことになります。そのため両端の2マスのうち内側はいずれ勝ち状態を相手に渡してしまうので負け状態で、それを相手に押し付けられる外側が勝ち状態です。

f:id:betrue12:20190420140008p:plain

こうして新しいルールを作ることができます。

駒5個以上の段において左右の端に未確定マスが横に2つ並び、勝ち状態に囲まれている場合、内側が負け状態で外側が勝ち状態である。

このルールにより、駒が6個以上の場合に対しても全ての状態を埋められるようになります。

Eで実験した何か pic.twitter.com/jCi4OvsVfG
— アルメリア (@armeria_betrue) April 19, 2019

あとは初期状態がどちらの状態かを判定すればよいです。図の規則性から3で割った余りで判定できるので、適切に式を立てて答えを出しましょう。例えば中心との距離を見ると偶数段/奇数段それぞれで共通の構成になっているので、私のコードはそれで判定しています。

「国王が先攻であるときにあなたが勝てるか」なので、初期状態が負け状態のときに YES を出力することに注意です。

ACコード

#340622 No.819 Enjapma game - yukicoder

2019-04-14

CSA FII Code Final Round Online Mirror F - Flawed Olympiad

CS Academy プログラミング競技プログラミング

https://csacademy.com/contest/fii-code-2019-final-round-online-mirror/task/flawed-olympiad/statement/

問題概要

要素数 $N$ の非負整数列 $A_{1}, ..., A_{N}$ と非負整数 $x$ が与えられる。数列 $A_{1}, ..., A_{N}$ の要素間に | （ビットOR）または & （ビットAND）を入れて出来る式であって、計算結果が $x$ となるものを1つ求めよ。そのような式が存在しない場合は impossible を出力せよ。

ここでORとANDの演算に優先順位はなく、左から順に処理されるものとする。

制約

$1\le N \le 10^{5}$
$0 \le x, A_{i} \lt 2^{30}$

解法

この記事では値同士の関係を、ビットが立っているところを要素とする集合の記号で表現することがあります。例えば $A \supseteq B$ は $B$ が $A$ の部分集合であること、つまり、 $B$ で立っている桁のビットは全て $A$ でも立っているという意味になります。

後ろから考える

最終的な計算結果に近いのは後ろの方の値なので、後ろから考えていきます。

一番後ろの要素である $A_{N}$ の直前に置く演算子としてANDを採用できる条件は、 $A_{N} \supseteq x$ であることです。

そして「ここにANDを採用したとき、 $A_{1}, ..., A_{N-1}$ の演算結果がどのような条件を満たすべきか」を考えることができて、具体的には

$A_{N}, x$ ともに0であるような桁については、どちらでもよい。
$A_{N}$ で1、 $x$ で0であるような桁については、0である必要がある。
$A_{N}, x$ ともに1であるような桁については、1である必要がある。

と判断することができます。

f:id:betrue12:20190414154527p:plain

一番後ろの要素である $A_{N}$ の直前に置く演算子としてORを採用できる条件は、逆に $A_{N} \subseteq x$ であることです。

そして同様に「ここにORを採用したとき、 $A_{1}, ..., A_{N-1}$ の演算結果がどのような条件を満たすべきか」については

$A_{N}, x$ ともに0であるような桁については、0である必要がある。
$A_{N}$ で0、 $x$ で1であるような桁については、1である必要がある。
$A_{N}, x$ ともに1であるような桁については、どちらでもよい。

と判断することができます。

f:id:betrue12:20190414155657p:plain

1つずつ決めていく

このように、OR/ANDそれぞれについて「その演算子を採用できる条件」と「その演算子を採用した場合、それ以前までの計算結果はどのような条件を満たすべきか」を求めることができます。これを繰り返していくことで後ろから順番に演算子を決めていくことができそうです。

後の説明のために定式化しておきましょう。 $dp\lbrack i \rbrack\lbrack d \rbrack$ を「 $A_{i}$ より後ろの演算子を決めた時、 $A_{1}, ..., A_{i}$ までの演算結果の $d$ 桁目はどのような状態になっているべきか」を表現する値とします。この値は「0である必要がある」「1である必要がある」「どちらでもよい」の3通りです。

遷移については、 $dp\lbrack i \rbrack$ と $A_{i}$ の値から $dp\lbrack i-1 \rbrack$ を更新します。一度「どちらでもよい」という扱いになった桁は無視することにして、先ほどと同じように考えて $A_{i}$ の直前の演算子を決定します。

OR/ANDのうちどちらかしか採用できない場合は単純にそちらを選び、どちらも採用できない場合はその時点で impossible と出力して終了します。問題なのはどちらも採用できる場合で、これを両方とも調べようとするとパターン数が爆発します。

OR/AND両方採用できる場合を考える

では、OR/AND両方採用できる場合というものが具体的にどうなっているか考えます。これは「どちらでもよい」桁を除いて $x$ と $dp\lbrack i \rbrack$ が一致している場合です。

このときもし $A_{i}$ の直前にANDを採用すれば、図で示すように $dp\lbrack i-1 \rbrack$ は「1である必要がある」桁と「どちらでもよい」桁だけになります。であれば、 $A_{i-1}$ までの値のビットはとにかく立てたほうが得なので、それ以前は全てORを採用するのが最善です。つまり $A_{0}, ..., A_{i-1}$ のORを計算してしまって「1である必要がある」ビットが全て立っていればそれが答えになりますし、そうでなければ $A_{i}$ の直前にANDを採用してはいけないことになります。

f:id:betrue12:20190414161224p:plain

同様に、もし $A_{i}$ の直前にORを採用すれば、 $dp\lbrack i-1 \rbrack$ は「0である必要がある」桁と「どちらでもよい」桁だけになります。そのため $A_{i-1}$ 以前は全てANDを採用するのが最善となり、それを計算することによって答えが得られるか $A_{i}$ の直前にORを採用してはいけないことが分かります。

f:id:betrue12:20190414162207p:plain

これにより各遷移は、「OR/ANDのうち片方だけに遷移する」「即座に答えが得られて終了する」「即座に impossible で終了する」のいずれかになり、結果として $O(N)$ で答えを求めることができます。

ACコード

CS Academy

本番コード、使ってない変数とか残っててあまりキレイじゃないです…

最初の要素をどう扱うかと、それに付随して $N=1$ の時の扱いが少し面倒だと思います。コードでは素直に場合分けしています。

2019-04-14

Codeforces Round #551 E. Serval and Snake

Codeforces プログラミング競技プログラミング

Problem - E - Codeforces

これ結構好き。

問題概要

インタラクティブ問題である。

$n \times n$ のグリッドがあり、グリッド内に蛇がいる。蛇の両端は異なるマスにあり、胴体は隣り合うマスを渡って両端を繋ぐパスとして表現される。

以下のクエリを2019回投げることが出来る。蛇の両端がどこのマスにあるか特定せよ。

グリッドの部分長方形をクエリとして指定する。返答として、蛇の胴体がその長方形の辺を横切る合計回数を得ることが出来る。

制約

$2 \le n \le 1000$

解法

胴体のパターン数は膨大にあり、胴体の形を考えようとすると破滅します。両端だけ求めれば良いので、これを直接求めます。

もし指定した長方形に蛇の両端のうち片方だけが入っていた場合、胴体が長方形の辺を横切る回数は奇数になります。入っていない場合と両方入っている場合は偶数になります。ここに着目します。

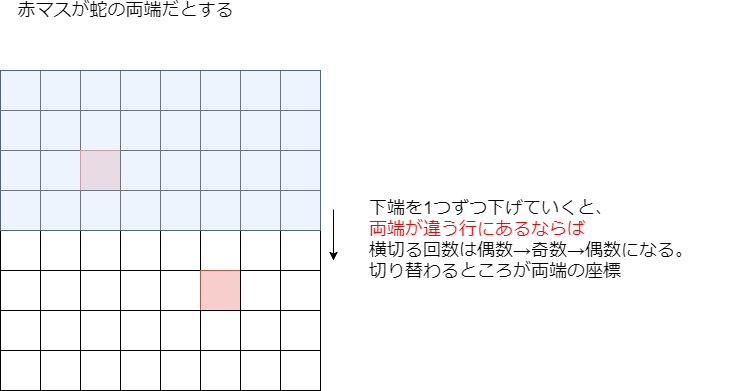
まず両端の行座標を特定します。以下の図のように、クエリの上・左・右の辺をグリッドの端に固定し、下の辺を1つずつ増やしていきます。こうすると、もし両端が同じ行にない場合は2つの行座標を特定することができます。これらの座標を $X_{1}, X_{2}$ としておきます。必要なクエリ数は $N$ 回です。（最後の1回は要らないので、 $N-1$ 回でも十分です）

f:id:betrue12:20190414140330p:plain

同様のことを列に対しても行います。もし両端が同じ列にない場合は2つの列座標を特定することができます。これらの座標を $Y_{1}, Y_{2}$ としておきます。やはり必要なクエリ数は $N$ 回です。

ここで両端は同じ座標にはないので、行と列のうち少なくとも片方は特定できていることになります。ここまでのクエリ数は $2N$ 回です。

どちらの座標も異なっていた場合

行と列どちらの座標も異なっていた場合、行座標が $X_{1}, X_{2}$ であり列座標が $Y_{1}, Y_{2}$ であると特定できています。あとはどっちとどっちが対応するか決まれば終わりです。

$(X_{1}, Y_{1})$ 1マスだけからなる長方形をクエリとして投げ、この返答が奇数であれば $(X_{1}, Y_{1}), (X_{2}, Y_{2})$ が答えです。返答が偶数であれば逆の組み合わせが答えです。

どちらかの座標が同じだった場合

行座標は異なっていて特定できたが、列座標が同じであるため特定できなかった場合を考えます。逆も同様です。

この場合、特定できた片方の行だけを見ると「どこかに1つだけ蛇の端点がある」状態になっています。そのため以下の図のように、左辺を端に固定して以下のように右辺を変えながらクエリを投げると、返答が奇数になる境目が蛇の端点の列座標です。これは2分探索できて $\lceil \log_{2} N \rceil$ 回のクエリで特定できます。

f:id:betrue12:20190414142345p:plain

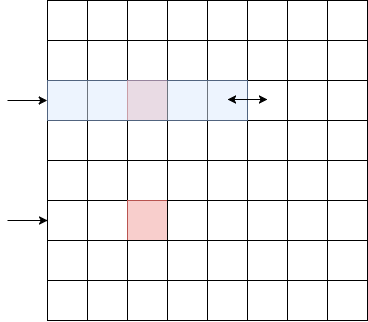
2つの端点の列座標は同じなので片方だけ特定すれば答えを求めることができます。

合計クエリ数は $2N + \lceil \log_{2} N \rceil$ で、 $N = 1000$ のとき2010回です。

ACコード

Submission #52701555 - Codeforces

上記の説明とは後半パートの長方形の取り方が少し違っていますが、処理の流れは同じです。

2019-04-07

AGC022 D - Shopping

AtCoder プログラミング競技プログラミング

D - Shopping

この記事を書いている時点で、AGC-Dの中で配点が最も高い問題。私自身AGC-Dを全問通しましたが、ダントツで一番難しい問題だと感じました。解説ACをするのにも非常に苦労しました…

この回は解説放送のアーカイブがなくて、解説記事も全然書かれていないようなので、高難度問題の解説に挑戦する意味でも書いてみたいと思います。

解法

周期で余りを取る

電車の総移動距離は電車の往復距離 $2L$ に往復回数を掛けた値なので、往復回数の最小値を求めることを考えます。

まず、ユイが買い物をしている時間 $t_{i}$ を電車の周期である $2L$ で割って余りを取ります。ここで減る分の時間は買い物をしている間に電車が往復しているだけなので、固定で掛かる往復回数として別途計算しておきます。ここで減らした往復回数の合計を $C$ とします。

ただし $t_{i}$ がちょうど $2L$ で割り切れるときは、 $0$ とせずに $2L$ だけ残しておいたほうが後々やりやすいです。

愚直なルートを考える

余りを取る操作によって $t_{i}$ は $1 \le t_{i} \le 2L$ の範囲に収まりました。このとき、以下のような愚直なルートを考えることができます。赤線がユイの移動、青破線が電車だけが動いているところを示します。

f:id:betrue12:20190407184320p:plain

図では途中の駅が4つあり、全部で5往復しています。一般にこのルートでは駅の数 $N$ に対して $N+1$ 回の往復が必要です。

このルートから短縮できるとしたら、どのようなルートになるかを考えていきます。

「買い物の後、端で反射してきた電車に乗れるか？」を考える

先ほどのルートでは、ユイが各駅に滞在している間に必ず電車が1往復していました。しかし実際には、一方の端で折り返して戻ってきた電車に間に合うこともあります。この場合は進行方向が反転します。

f:id:betrue12:20190407192715p:plain

折り返してきた電車に間に合うための条件は、左から入った時（右で折り返す時）と右から入った時（左で折り返す時）で異なります。後の説明の都合から、折り返す方向で区別することにします。具体的には右で折り返す時に間に合う条件は $t_{i} \le 2(L-x_{i})$ であり、左で折り返す時に間に合う条件は $t_{i} \le 2x_{i}$ です。

これを利用してルートの短縮ができないか考えます。

ルート短縮方法を考える

ルート短縮方法は、大きく分けると2つあります。

まず1つ目として、一番右にある駅が「右で折り返す時に間に合う」駅だった場合に、以下のようなルートにすることで往復を1回減らすことができます。元のルートでは「ユイが電車に乗ったまま右端に到達する」ということが1回ありましたが、それが無くなることで無駄を省いています。

f:id:betrue12:20190407184332p:plain

次に2つ目として、「左で折り返す時に間に合う」駅と「右で折り返す時に間に合う」駅がこの順番で並んでいる時に、以下のようなルートにすることで往復回数を1回減らすことができます。

f:id:betrue12:20190407184347p:plain

このように「ユイを右端に到達させないことで往復回数を減らす」「左右で1回ずつ折り返しに間に合わせることで往復回数を減らす」の2つの短縮方法があり、これ以外にはありません。そのため元のルートを短縮するような全てのルートは、並び替えると上の2パターンのどちらかと同じになります。（本当はここの証明をちゃんとやらないといけないですね…）

なので元々の往復回数 $N+1$ から始めて、以下のように減らせる回数を考えればそれが最適解となります。

まず一番右の駅が「左から入った時に折返しに間に合う」駅なら、往復回数を1減らす。そうした場合、この駅は2. で使うことはできない。
次に「左で折り返す時に間に合う」駅と「右で折り返す時に間に合う」駅がこの順番で並んでいるようなペアをできるだけ多く作る。

あとはペアをできるだけ多く作る方法を考えれば解くことができます。

ペアの最適な作り方を考える

先ほど見たように、右で折り返す時に間に合う条件は $t_{i} \le 2(L-x_{i})$ であり、左で折り返す時に間に合う条件は $t_{i} \le 2x_{i}$ です。まずこれを全ての駅について計算します。

基本的には左から順番に見て貪欲に組んでいけば良いです。つまり「左で折り返す時に間に合う」駅をストックしておき、「右で折り返す時に間に合う」駅が登場した時点でペアにします。

ただし左右どちらで折り返しても間に合うような駅を左右どちらで使うかは注意する必要があります。これを適切に使うためには、

「右で折り返す時に間に合う」駅に対してペアを作る時には、「左で折り返す時だけ間に合う」駅を優先的に使うようにする。
「左右どちらで折り返しても間に合うような駅」同士のペアはすぐには作らずにストックしておき、一番最後に余ったものをペアにする。

ようにすれば最適な組み方になります。

このようにして往復回数の最小値を求めることが出来るので、固定で掛かる往復回数 $C$ を足し、距離に直すために $2L$ 倍したものが答えになります。

ACコード

私のACコードです。

Submission #4874656 - AtCoder Grand Contest 022

参考にしたのはFirst ACのこのコードです。

Submission #2287052 - AtCoder Grand Contest 022

とても読みやすい。先ほどの説明の中で「左右どちらで折り返しても間に合うような駅」の扱いに注意する必要があると書きましたが、このコードでは左で使うものと右で使うものの境界を二分探索っぽく求めているように見えます。

2019-03-31

エクサウィザーズ 2019 E - Black or White

AtCoder プログラミング競技プログラミング

E - Black or White

解法

答えを定式化する

$i$ 番目のチョコレートを食べ終わった直後に、

黒が残っている確率： $p_{b, i}$
黒白どちらも残っている確率： $p_{bw, i}$

とします。このとき黒だけが残っている確率は $p_{b, i} - p_{bw, i}$ です。

$i$ 番目に食べるチョコレートが黒であるパターンは、

$i-1$ 番目のチョコレートまで食べ終わった直後、黒だけが残っている。
$i-1$ 番目のチョコレートまで食べ終わった直後、黒白どちらも残っていて、 $\frac{1}{2}$ の選択で黒を選ぶ。

のどちらかなので、その確率は $(p_{b, i-1} - p_{bw, i-1}) + \frac{1}{2}p_{bw, i-1}$ で求めることができます。

計算に必要な確率を求める

計算に必要な確率 $p_{b, i}$ と $p_{bw, i}$ を求めましょう。

片方のチョコが切れた後の考え方を簡単にするため、問題を少し言い換えます。

すぬけ君はチョコを1個食べようとするごとに、必ずちょうど1回 黒か白を等確率で選ぶ。選んだ方のチョコがある場合はそちらを食べ、ない場合は選択に関わらず残っている色のチョコを食べる。

この言い換えによって、 $i$ 番目のチョコを食べ終わった直後までに色を選んだ回数が必ず $i$ 回となります。

黒が残っている確率は、この $i$ 回の選択で黒を選んだ回数が $B-1$ 回以下である確率になります。その確率は

$p_{b, i} = (\frac{1}{2})^{i} \times (_{i-1}C_{0} + _{i}C_{1} + \cdots + _{i}C_{B-1})$

となります。

同様に白黒どちらも残っている確率は、黒を選んだ回数が $B-1$ 回以下かつ白を選んだ回数が $W-1$ 回以下である確率になります。黒白の合計が $i$ 回なので、計算すると黒を選んだ回数は $i-(W-1)$ 回以上 $B-1$ 回以下です。その確率は

$p_{bw, i} = (\frac{1}{2})^{i} \times (_{i}C_{i-(W-1)} + \cdots + _{i}C_{B-1})$

となります。（左右それぞれ、 $\lbrack 0, i\rbrack$ の範囲外のものは無視します）

これを全ての $i$ について計算したいのですが、毎回全部計算していては間に合いません。これを計算するためにパスカルの三角形を使います。

頭に付いている $\frac{1}{2}$ の累乗は最後に掛けることにして、二項係数の部分だけ考えます。 $p_{b, i}$ の二項係数の部分を $c_{b, i}$ とします。

f:id:betrue12:20190331094914p:plain

求めたい値は図のように、パスカルの三角形の各段における連続した要素和になります。1つ前の段に注目すると、ほとんどの値については2方向に値が足されるので次の段では2倍されます。唯一 $_{i-1}C_{B-1}$ だけについては、右側の遷移先が範囲外になるので2倍されません。

このことから以下の漸化式が成り立ちます。

$c_{b, i} = 2c_{b, i-1} - _{i-1}C_{B-1}$

$p_{bw, i}$ に対しても同様に、右側に加えて左側についても範囲から外れるところの値を処理することによって、二項係数の和を計算する漸化式を立てることができます。これらの確率が計算できれば、最初に示した式で答えを求めることができます。

ACコード

Submission #4774057 - ExaWizards 2019

有理数を素数modで出力する形式はAtCoderではなかなか見ないですが、Codeforcesではよく見ます。四則演算については割り算として逆元を用いることにして普通に計算すれば大丈夫です。

2019-03-31

エクサウィザーズ 2019 D - Modulo Operations

AtCoder プログラミング競技プログラミング

D - Modulo Operations

解法

単調減少列を考える

まず気付くべき点は、「ある値 $a$ で余りを取ったあと、それより大きい値 $b$ で余りを取っても値は変化しない」ということです。 $a$ で余りを取った時点で黒板に書かれた値 $x$ は $a-1$ 以下になっていて、その $x$ より大きい値で余りを取っても $x$ の値は変化しません。

このことから余りを取る操作列が1つ決まった時、実際に最後に残る値に影響するのは操作列から「それまでに登場した中で一番小さな値」だけを抜き出した単調減少列の並びだけであることが分かります。

f:id:betrue12:20190331080432p:plain

操作列からこのように抜き出される単調減少列を「実質的操作列」と呼ぶことにします。実質的操作列が同じ操作列は結果が同じになるのでまとめて考えることができます。例えば

$11 \to 13 \to 6 \to 22 \to 5$
$11 \to 6 \to 5 \to 22 \to 13$

この2つの操作列の実質的操作列はどちらも $11 \to 6 \to 5$ になり、まとめて考えることができます。

ある実質的操作列になる操作列の個数を考える

では、ある実質的操作列に対応する操作列は何通りあるでしょうか。

与えられた全ての $S_{i}$ を降順にソートしておきます。実質的操作列としてあり得るものは、この降順ソートした数列から1個以上の要素を採用したものです。ここで「採用しなかった要素」は、自分より小さいどれかの要素の後ろに付くことになります。このときの選択肢の数によって操作列の個数が増えていきます。

f:id:betrue12:20190331082242p:plain

上の図のように考えると、ある実質的操作列に対応する操作列の個数は「採用しなかった要素について、それより小さい要素の個数を掛け算したもの」であることが分かります。

これを言い換えると、「降順にソートした数列を順に見ていって、 $i$ 番目にある要素を採用しないと決めた時、場合の数は $N-i$ 倍される」と考えることができます（1-indexedです）。これが後のDPに繋がります。

DPする

降順ソートした列を順に見ていくDPができないか考えます。DPテーブルを「 $i$ 番目まで見た時に○○である場合の数」とするのは良いとして、何を状態として持つべきでしょうか。

操作を適用していくのはその時点で黒板に書かれた数 $x$ に対してなので、これを状態として持つことができないか考えます。 $x$ の値は初期値 $X$ 以下であり、 $N \le 200$ かつ $X \le 10^{5}$ という条件から $O(NX)$ が間に合いそうです。 $x$ を状態として持ってしまいましょう。

$dp\lbrack i \rbrack \lbrack x \rbrack =$ 降順ソートした数列 $i$ 番目まで見て、その時点での黒板に書かれた値が $x$ であるような場合の数

$dp\lbrack i \rbrack \lbrack x \rbrack$ からの遷移を考えます。遷移は $i+1$ 番目の要素を実質的操作列として採用するかしないかの2通りで考えることができます。

採用する場合は、余りを取って $dp\lbrack i+1 \rbrack\lbrack x\%S_{i+1}\rbrack$ に遷移します。
採用しない場合は、先ほど見たように場合の数を $N-(i+1)$ 倍した上で $dp\lbrack i+1 \rbrack\lbrack x\rbrack$ に遷移します。

これを最後まで計算すると各 $x$ について「最後に書かれた値が $x$ になるような場合の数」を求められるので、答えを計算できます。

ACコード

Submission #4771085 - ExaWizards 2019

コンテスト本番コード。考察の過程で出てきたけど使わなかった階乗ライブラリが貼りっぱなしになっています（？）

公式解説では確率（期待値）の問題に置き換えて計算をしていますが、私自身が本番では場合の数ベースで考察をしたため、この記事でも場合の数ベースで解説しました。

2019-03-24

ABC122 D - We Like AGC

AtCoder プログラミング競技プログラミング

D - We Like AGC

解法

問題文の条件を満たすためには、具体的にどのような部分文字列が含まれていてはダメでしょうか。NGパターンを列挙してみましょう。

3文字のNGパターン
- もちろん AGC はNGです。また、隣り合う2文字を入れ替えて AGC となる GAC と ACG もNGです。3文字のNGパターンはこれで全部です。
4文字のNGパターン
- X を任意の文字として AXGC はNGパターンです。最初の2文字を入れ替えると AGC ができてしまうからです。同様の理由で AGXC もNGです。4文字のNGパターンはこれで全部です。

列挙してみると意外と少ないことが分かります。また5文字以上のNGパターンはありません。「隣り合う2文字の入れ替えを高々1回行って、連続する3文字の並びを見る」という操作に関係する文字は、必ず連続する4文字以内に収まっているからです。

ということで、連続する4文字の並びを確認すればNGパターンかどうかが判定できることが分かりました。これを言い換えると

文字列の末尾に新しく1つ文字を足した時にNGパターンが新しく発生しないかどうかは、直近の3文字だけを見れば判定できる

ということになります。この考え方を元にDPを構成することが出来ます。

具体的には、

$dp\lbrack i \rbrack\lbrack a \rbrack\lbrack b \rbrack\lbrack c \rbrack =$ $i$ 文字までの文字を決めていて、最近の3文字が左から $a, b, c$ となっていて、NGパターンを含んでいない文字列の場合の数

という状態を持ってDPすることができます。 $a, b, c$ はそれぞれ文字 TAGC のどれかだと思ってください（後で実装について補足します）。

$dp\lbrack i \rbrack\lbrack a \rbrack\lbrack b \rbrack\lbrack c \rbrack$ からの遷移を考えます。この文字列に文字 $d$ を足した時に新しく発生するNGパターンは、先ほど列挙した通り

3文字のNGパターン
- 文字列 $bcd$ が、AGC GAC ACG のどれか
4文字のNGパターン
- 文字列 $abcd$ が、X を任意の文字として AXGC AGXC のどちらか

です。これらNGパターンのどれにも当てはまらなければ、 $dp\lbrack i+1 \rbrack\lbrack b \rbrack\lbrack c \rbrack\lbrack d \rbrack$ に遷移することが出来ます。

このDPを全部計算して、最後に $dp\lbrack N \rbrack\lbrack a \rbrack\lbrack b \rbrack\lbrack c \rbrack$ を全ての $a, b, c$ について合計したものが答えとなります。

ACコード＆実装の補足

Submission #4700029 - AtCoder Beginner Contest 122

実装について少し補足します。まず先ほどの説明では文字をDPテーブルの添字として扱っていましたが、実装においては 0123 といった整数に対応させましょう。私のコードでは添字の 0123 が順に TAGC に対応しています。

次に初期状態について。DPの初期条件を考える時、初期状態（空文字列）には「直近の3文字」がないので少し困ります。今回の場合は「NGパターンに関して意味を持たないような文字」、つまり T が存在すると見なしてしまって良いです。先ほど T は添字 0 に対応させていたので、初期条件を dp[0][0][0][0] = 1 としています。

最後に関数 add(a, b) について。私のコードでは「変数 a に変数 b の値を足してMODを取る」という処理を add(a, b) にやらせています。a = (a+b) % MOD と同等の機能です。