2019-10-12

Educational Codeforces Round 74 E. Keyboard Purchase

お題箱より。ただ、この問題は元々書こうと思っていました。

問題概要

$m$ 文字のアルファベットからなる長さ $n$ の文字列 $S$ が与えられる。アルファベット $m$ 個を並べる順列 $P$ を1つ決めた時、「 $S$ の隣り合う2文字のペアそれぞれについて、そのアルファベット2つの $P$ での距離を求め、合計したもの」を合計コストとする。この合計コストの最小値を求めよ。

制約

$1 \le n \le 10^{5}$
$1 \le m \le 20$

解法

まず異なるアルファベットのペア $\frac{m(m-1)}{2}$ 通りについて、そのペアが $S$ において何回隣り合っているかを前もって集計しておきます。こうすれば以降の計算で文字列の長さ $n$ は関係なくなります。アルファベットのペア $(x, y)$ に対するペアの登場回数を $c(x, y)$ と書くことにします。これは隣り合っている順番を区別せず両方含むことにします、すなわち $c(x, y) = c(y, x)$ です。

また順列 $P$ 上での $(x, y)$ の距離を $d(x, y)$ と書くことにします。そうすると合計コストは $c(x, y) \times d(x, y)$ を全てのペアについて合計したものです。

順列 $P$ に並べるアルファベットを順に1つずつ決めていくようなDPを考えてみます。このとき単純に考えると、アルファベットを足したことによるコストの増加量を「新しく追加したアルファベット $y$ と既に追加済みのアルファベット $x$ たちについて、 $c(x, y) \times d(x, y)$ を足す」と計算したくなります。ただし $d(x, y)$ を計算するには既に追加したアルファベットの順番を覚えておく必要があり、状態数が爆発します。

f:id:betrue12:20191012024502p:plain

何とかして順番を覚えなくても良いようにしたいです。順番を忘れることができれば、これは集合に対するDP、つまり状態数が $2^{m}$ になるようなbit DPとして解けそうです。

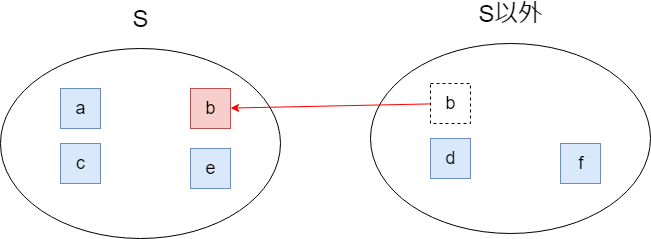
ここで発想を変えましょう。「アルファベットを1つ足そうとして、 $P$ の置き場所の境目を1つまたぐときに、追加済みのアルファベットと未追加のアルファベットのペア全部について距離が1増える」と考えます。言わんとすることは図を見てください。

f:id:betrue12:20191012025028p:plain

こうするとペア数自体は多くなってしまうのですが、「追加済みのアルファベット」を一括りにできるので順番を覚えておく必要がなくなります。

こうやって計算されるコストの増加量は、アルファベットの集合 $S$ に対する「 $S$ に含まれる要素 $x$ と含まれない要素 $y$ を組み合わせた全てのペアについての、 $c(x, y)$ の合計値」です。この値を $C(S)$ と書くことにすると、DPの遷移は

集合 $S$ を遷移元として、 $S$ 含まれていない要素 $y$ それぞれについて、 $dp\lbrack S \cup \lbrace y \rbrace \rbrack \leftarrow dp\lbrack S \rbrack + C(S)$ と更新（より小さかったら採用）する

と行うことが出来ます。ここでDPテーブルの定義は、「集合 $S$ に含まれている要素を既に並べていて、既に通り過ぎた境目について、アルファベットのペアがそこをまたぐ時のコスト増加量を合計したものの最小値」です。

遷移の合計回数が $O(m2^{m})$ なので、あとは $C(S)$ を良い感じに前計算できれば間に合いそうです。

$C(S)$ の前計算は、こちらも $S$ の状態数が $2^{m}$ なので1個あたり $O(m)$ くらいで計算できれば勝ちです。これもDPで計算できます。

ある集合 $S$ について既に $C(S)$ が求まっているとします。ここで $S$ に含まれていない要素 $y$ を新しく $S$ に足すと、 $C(S)$ に対する変化量は

$S$ に含まれている要素 $x$ について、 $(x, y)$ が新たに同じ集合に入るので $c(x, y)$ が減算される。
$S$ に含まれていない $y$ 以外の要素 $z$ について、 $(y, z)$ が違う集合に分かれるので $c(z, y)$ が加算される。

として計算できるので、 $C(S)$ から $C(S\cup \lbrace y \rbrace)$ を差分計算できます。これは $O(m)$ でできます。

f:id:betrue12:20191012024928p:plain

これで前計算も $O(m2^{m})$ で出来たので、間に合います。

ACコード

Submission #62145546 - Codeforces

数え上げ問題で、よく「全てのAについてのBの合計を求めよ」という問題を「Bの加算要素それぞれについて、それが含まれるAの個数を掛けたものの合計を求めよ」と言い換えるものがあります。今回も「アルファベットのペア」と「 $P$ における置き場所の境目」について同じことをしている、と考えることが出来ますね。

2019-10-09

第一回日本最強プログラマー学生選手権決勝 C - Maximize Minimum

AtCoder プログラミング競技プログラミング

お題箱より。同じ問題に2件リクエストがありました。

C - Maximize Minimum

簡潔に飛ばし気味ではあるものの公式解説の説明が分かりやすいと思うので、流れは公式解説に沿いつつ図や行間を補って書いていきます。

解法

イチゴの最適な折り返し方

まずクエリについては忘れます。「ケーキを左半分と右半分で鏡写しのように見たときに、イチゴを何回でも反対側に折り返していいので、一番近いイチゴ間の距離をできるだけ遠くしてください」という問題です。

何回でも折り返していいので、まずは左半分の側に全てのイチゴをまとめて、それからいくつかのイチゴを選んで折り返す最適な選び方を考えてみましょう。イチゴの個数を $k$ として、左側に全てまとめたときのイチゴの座標を小さい方から $b_{0}, b_{1}, ..., b_{k-1}$ とします。ここで $b_{i} \le \frac{L}{2}$ です。

まず簡単なケースから考えましょう。以下のようにイチゴが間隔1で等間隔に並んでいて、ケーキが十分長いようなケースです。

f:id:betrue12:20191009231447p:plain

このときの最適な並べ方は、 $b_{1}, b_{3}, b_{5}, ...$ のイチゴを折り返すことです。つまり座標の小さいものから左右交互に配置していきます。

f:id:betrue12:20191009231505p:plain

こうすることで一番近い距離が2になります。もし交互になっていないところがあると距離1が登場してしまうので、これが最適です。

この「全部片側に寄せて、座標の小さいものから左右交互」という考え方を実は一般化できて、このような置き方が常に最適になります。そのときのイチゴ間の距離は、 $b_{0}, b_{1}, ..., b_{k-1}$ を用いると

1つ飛ばしでのイチゴの距離 $b_{2}-b_{0}, b_{3}-b_{1}, ..., b_{n-1} - b_{n-3}$
最も右側（ケーキの中心）に近い2つのイチゴを、左右逆側に配置した時の距離 $L - b_{n-1} - b_{n-2}$

になります（2.を忘れがちなので注意ですね）。これらのうち最も小さい値が答えになります。

最適性の証明は公式解説の通りです。連続する3つのイチゴ $b_{i}, b_{i+1}, b_{i+2}$ を考えると、これらのうちどれか2個のペアは左右同じ側に置かないといけないので、 $b_{i+1}-b_{i}, b_{i+2}-b_{i+1}, b_{i+2}-b_{i}$ の少なくとも1つはイチゴ間の距離として採用しないといけません。それならば、この中で一番大きい $b_{i+2}-b_{i}$ を常に採用する左右交互の並べ方が最適ということになります。

2.の最も右側のイチゴ2つを左右同じ側ではなく左右逆側に配置したほうが常に得であることも、逆側に配置したときの距離 $L - b_{n-1} - b_{n-2}$ と同じ側に配置した時の距離 $b_{n-1} - b_{n-2}$ の大小を評価すれば分かります。（ $b_{i} \le \frac{L}{2}$ であることを使います）

クエリの処理を考える

ではクエリの処理方法を考えます。

まずは各クエリでイチゴを入れるのか除くのか判断するため、今あるイチゴの「元の」座標を管理する集合1を作ります。

それとは別に、折り返した座標である $b_{0}, b_{1}, ..., b_{k-1}$ を管理できる集合2を作ります。鏡写しで同じ座標にイチゴが2個あることもあるので、多重集合のほうが適しています。

各クエリでは集合1を使って要素を出すのか入れるのか判断し、集合1, 2に要素を出し入れします。そして答えを求めるために「1つ飛ばしでのイチゴの距離」のうち最も小さいものを求める必要があります。これは以下のようにして求めることができます。

集合2を順序付き多重集合（C++の multiset など）として持ち、常に要素がソートされているようにします。そうすると要素を1個挿入または削除したときには、「1つ飛ばしでのイチゴの距離」はその周囲でだけ変化します。具体的には当該要素の左側2つ・右側2つまでの座標だけ分かれば、変化する値は以下のように計算できます。

f:id:betrue12:20191009232547p:plain

つまり1回のクエリは、「その時点での "1つ飛ばしでのイチゴの距離" たちの集合」に対する高々5個の要素の出し入れとして処理できます。これも multiset として管理しておけば、各操作の後にその最小値を求めることができます。

multiset において「ある要素の2つ左の要素」などを求めるには、いったん lower_bound などでその要素の場所を求めた後にイテレータ操作をすれば良いです。順序付き集合が標準で存在しない言語の場合は、自前の平衡二分探索木を使うか座標圧縮＋セグメント木＋二分探索などの処理が必要になると思われます…。

これで1つ飛ばしでのイチゴの距離の最小値が分かります。また集合2の大きいほうから2要素を見ることで $L - x_{n-1} - x_{n-2}$ も計算できます。これで各クエリに $O(\log N)$ で答えることができて間に合います。

ACコード

Submission #7801071 - 第一回日本最強プログラマー学生選手権決勝(オープンコンテスト)

実装も、「慣れ」が必要なタイプだと思います。特に集合2の操作時に周囲の要素を見るときは、それが端っこだったりすると場合分けが面倒なので番兵などを使っていますが…読む分には逆に謎の値がいきなり登場して分かりにくいかもしれません。

2019-10-06

Kodamanと愉快な仲間たち S - 五等分の分銅

プログラミング競技プログラミング

お題箱より。

Programming Problems and Competitions :: HackerRank

解法

分数のままでは考えにくいので、通分します。 $1, 2, 3, 4, 5$ の最大公約数は $60$ なので、まず重りを全て $60$ 倍して $60, 30, 20, 15, 12$ とします。そして目標の重さも $S = \frac{60p}{q}$ に置き換えます。するとこの問題は「重さ $60, 30, 20, 15, 12$ の重りをそれぞれ $a, b, c, d, e$ 個以下使って合計 $S$ を作る場合の数を求めよ」という問題と見なせます。もし $S$ が整数にならない場合は0通りです。

これは「部分和問題」と呼ばれるもので、特に今回は

個数制限付き：各要素が何個まで使えるか指定されている
数え上げ： $S$ が作れるかどうかの判定だけでなく、その作り方の場合の数を求める必要がある

という特徴があります。

これを公式解説のDPで解きます。以下のようなDPテーブルを定義します。

$dp\lbrack i \rbrack\lbrack s\rbrack =$ 重り $i$ までの使い方を決めて、その合計が $s$ であるような重りの使い方の場合の数

この遷移を具体例で説明します。重り $i$ の重さが $60$ で、これが $2$ 個まで使えるとします。このときの $i-1$ から $i$ からの更新方法を考えます。

更新の順番として、 $\bmod 60$ ごとに更新をしていくという方法を取ります。つまり

$dp\lbrack i \rbrack\lbrack 0 \rbrack, dp\lbrack i \rbrack\lbrack 60 \rbrack, dp\lbrack i \rbrack\lbrack 120 \rbrack, ...$ をこの順に更新する。
$dp\lbrack i \rbrack\lbrack 1 \rbrack, dp\lbrack i \rbrack\lbrack 61 \rbrack, dp\lbrack i \rbrack\lbrack 121 \rbrack, ...$ をこの順に更新する。
…
$dp\lbrack i \rbrack\lbrack 59 \rbrack, dp\lbrack i \rbrack\lbrack 119 \rbrack, dp\lbrack i \rbrack\lbrack 179 \rbrack, ...$ をこの順に更新する。

という流れです。

いま重さ $60$ の重りを $2$ 個まで使える場合を考えているので、 $dp\lbrack i \rbrack\lbrack s \rbrack$ に遷移できるのは $dp\lbrack i-1 \rbrack\lbrack s \rbrack, dp\lbrack i-1 \rbrack\lbrack s-60 \rbrack, dp\lbrack i-1 \rbrack\lbrack s-120 \rbrack$ の3点からです。例えば $0, 60, 120, ...$ を更新する時には、以下の図のような遷移になります。

つまり遷移元が一定の長さを保ったままスライドしていくので、例えば $dp\lbrack i \rbrack\lbrack 180 \rbrack$ の遷移元と $dp\lbrack i \rbrack\lbrack 240 \rbrack$ の遷移元の違いは両端だけです。このように範囲に入るものと出るものを差分更新することで、遷移元の値を効率的に管理することが出来ます。（解説の「しゃく取り法っぽく」はこれを指しています）

このようにすれば重り1種類についての遷移の計算量は $O(S)$ です。 $\bmod$ で分類しているだけで結局は遷移先の $0, ..., S$ を1回ずつ見ていることになり、遷移元の計算は差分更新で毎回 $O(1)$ でできているからです。重りの種類数を $N$ として全体計算量は $O(NS)$ になります。今回の問題では $N=5$ であり、 $S = \frac{60p}{q}$ は制約より600万以下です。

ACコード

HackerRankは提出が非公開らしいので、ベタ書きします。

#include <bits/stdc++.h>
using namespace std;

int main(){
    int A[5], P, Q;
    for(int i=0; i<5; i++) cin >> A[i];
    int W[5] = {60, 30, 20, 15, 12};
    cin >> P >> Q;
    if(60%Q){
        cout << 0 << endl;
        return 0;
    }
    int S = P*60/Q;

    static int64_t dp[6][6000001];
    dp[0][0] = 1;
    for(int i=0; i<5; i++){
        for(int r=0; r<W[i]; r++){
            int64_t sum = 0;
            for(int s=r; s<=S; s+=W[i]){
                sum += dp[i][s];
                int out = s - (A[i]+1)*W[i];
                if(out >= 0) sum -= dp[i][out];
                dp[i+1][s] = sum;
            }
        }
    }
    cout << dp[5][S] << endl;
    return 0;
}

2019-10-03

AtCoder Beginner Contest 054 D - Mixing Experiment

AtCoder プログラミング競技プログラミング

お題箱より。

D - Mixing Experiment

半分全列挙解法を…とのリクエストだったので、そちらを書きます。

解法

$N$ 個の薬品をグループ0・グループ1に分け、それぞれについて薬品の選び方を決めたとします。これらを混ぜてちょうど混合比 $M_{a}:M_{b}$ になっているかどうかを判定する式を立てましょう。

グループ $g$ で選んだ薬品に含まれるタイプAの薬品量を $A_{g}$ 、タイプBの薬品量を $B_{g}$ と表記することにします（ $g$ は $0$ または $1$ ）。両グループの薬品を混ぜて混合比が $M_{a}:M_{b}$ となる条件は

$\displaystyle\frac{A_{0}+A_{1}}{B_{0}+B_{1}} = \frac{M_{a}}{M_{b}}$

という数式で表現できます。これを通分すると

$M_{b}A_{0} + M_{b}A_{1} = M_{a} B_{0} + M_{a}B_{1}$

となりますが、さらにこれを移項して並び替えると

$(M_{b}A_{0} - M_{a}B_{0}) + (M_{b}A_{1} - M_{a}B_{1}) = 0$

となります。このように変形した目的は、グループ0に関する値とグループ1に関する値に分離するためです。

つまり両グループで選んだ薬品を混ぜて欲しい混合比になる条件は、グループ $g$ に対して $S_{g} = M_{b}A_{g} - M_{a}B_{g}$ と定義すると、 $S_{0} + S_{1} = 0$ という数式で表現できます。これはつまり、それぞれのグループで薬品の選び方を決めた時の具体的な薬品量は忘れてしまって良くて、 $S_{g}$ の値さえ覚えておけば判定ができるということです。

求めたいのは欲しい混合比になるための最小価格でした。なのでそれぞれのグループごとに選び方を全列挙して、以下の値を求めます。

$C\lbrack g \rbrack\lbrack s \rbrack =$ グループ $g$ の薬品を1つ以上選んで、その薬品量 $A_{g}, B_{g}$ について $M_{b}A_{g} - M_{a}B_{g}$ の値が $s$ となるときの、最小の合計価格。ただしそのような選び方が存在しない場合はINFとする。

1つ以上という点に注意しないといけない理由は、この条件を考慮しないと両グループともに薬品を1つも選ばないケースが含まれてしまうからです。薬品を1つも選ばないと $S_{0} + S_{1} = 0$ は必ず満たされてしまうので、合計価格0が必ず答えに出てきてしまいます。

欲しい混合比を作れる最小の価格は、以下の3パターンのうちの最も小さいものになります。ただし全ての結果がINF以上になってしまった場合は、ほしい混合比を作れる薬品の選び方は存在しません。

グループ0に属する薬品だけで作る場合。その価格は $C\lbrack 0 \rbrack\lbrack 0 \rbrack$ である。
グループ1に属する薬品だけで作る場合。その価格は $C\lbrack 1 \rbrack\lbrack 0 \rbrack$ である。
両グループの薬品をともに1つ以上選ぶ場合。その価格は取りうる全ての $s$ に対する $C\lbrack 0 \rbrack\lbrack s \rbrack + C\lbrack 1 \rbrack\lbrack -s \rbrack$ の最小値である。

これで解くことができました。ポイントは判定式を立てた後に項をグループごとに分離する、以下の形への式変形ですね。

$(M_{b}A_{0} - M_{a}B_{0}) + (M_{b}A_{1} - M_{a}B_{1}) = 0$

ACコード

$C\lbrack g \rbrack\lbrack s \rbrack$ において $s$ が負になるため、実装上は負のインデックスを回避しないといけません。最小値が0以上になるように固定値を足して管理する（オフセット）か、mapを使うかのどちらかが良いと思います。mapを使うと計算量に $\log$ が追加で乗る点には注意しましょう。

オフセット：Submission #7837503 - AtCoder Beginner Contest 054
map：Submission #7837514 - AtCoder Beginner Contest 054

2019-09-24

Codeforces Round #587 (Div. 3) F. Wi-Fi

Codeforces プログラミング競技プログラミング

お題箱より。

Problem - F - Codeforces

セグメント木を使わない解法を…とのリクエストだったので、何通りか解法を紹介します。

問題概要

$n$ 個の部屋が並んでいて、順に番号 $1, ..., n$ が付けられている。これらの部屋全てにインターネット回線を提供したい。

回線提供には2つの方法がある。

それぞれの部屋 $i$ について、 $i$ コイン払うことでその部屋に単独でインターネット回線を提供できる。
いくつかの部屋は無線ルーターを持っていて、その部屋 $i$ については $i$ コイン払うことで区間 $\lbrack \max(1, i-k), \min(N, i+k)\rbrack$ に含まれる全ての部屋にインターネット回線を提供できる。

整数 $n, k$ と各部屋の無線ルーターの所持有無が与えられるので、全ての部屋にインターネット回線を提供するために払う合計コインの最小値を求めよ。

制約

$1 \le n, k \le 2\times 10^{5}$

解法1：セグメント木

この問題は結局、

（区間, その区間を使うコスト）の組がいくつか与えられるので、整数点 $1, ..., n$ 全てを覆う最小コストを求めよ。

という問題です。この問題をパターンとして捉えセグメント木で処理するのがたぶん一番楽です。

$dp\lbrack i \rbrack$ を「整数点 $1, ..., i$ が全て覆われるための最小コスト」とします。予め区間を右端で分類しておき、 $dp\lbrack i \rbrack$ を更新するときには $i$ を右端とするような区間それぞれに対して、

その区間の左端を $l$ 、コストを $c$ とするとき、 $\min(dp\lbrack l-1 \rbrack, ..., dp\lbrack i-1 \rbrack) + c$ で $dp\lbrack i \rbrack$ を更新（今の値より小さければ採用）する

とすれば良いです。少なくとも $l-1$ までが覆われている状態を遷移元とすることで、区間 $\lbrack l, i\rbrack$ を新たに採用して $i$ までを覆うことができます。

区間最小が取れるセグメント木にDPの値を入れることで高速に $\min$ の計算ができます。セグメント木のクエリ1回が $O(\log n)$ なので全体計算量は $O(n\log n)$ です。

この解法は後に紹介するようなこの問題特有の単調性が無くても使えるので、そういった意味でもこの解法を知っておくのがオススメです。

ACコード1

Submission #60990629 - Codeforces

解法2：スライド最小値

ルーターが覆う区間の長さは左右にはみ出る場合を除けば一定で、ルーターを置く部屋を右にずらしていくと左端も右端も単調に変化します。このような場合、先ほどの $\min(dp\lbrack l-1 \rbrack, ..., dp\lbrack i-1 \rbrack)$ の計算はスライド最小値という方法を用いて高速化できます。この場合、計算量はDP全体でならし $O(n)$ となります。

ルーターを使わない場合の遷移は単に1つ前の1点だけが遷移元になるので各点ごとに $O(1)$ で計算できます。結局全体で $O(n)$ になります。

ACコード2

Submission #61186419 - Codeforces

解法3：コストの単調性を使ってgreedy

リクエスト的にはこれが本命ですかね。このコメントを参考にしました。今回の場合はコストが右の部屋にいくほど高くなっているので、DPの遷移をgreedyに取ることができます。

DPを左（添え字の小さい方）から回すのではなく、右から回します。 $dp\lbrack i \rbrack$ を「整数点 $i, ..., N$ が全て覆われるための最小コスト」と定義します。

$dp\lbrack i+1 \rbrack$ から $dp\lbrack i \rbrack$ 方向への遷移を考えます。つまり右から $i+1$ までが覆われているので、次に採用する区間で少なくとも $i$ は覆う必要があります。

1つの方法は単に部屋 $i$ 単独で回線を引くことです。そしてルーターに関しては、実は部屋 $i$ をカバー範囲に含むルーターのうち最も左にあるものだけを考えれば十分です。これがまだカバーされていない範囲を最も遠くまでカバーし、加えて左側の部屋のルーターを使ったほうがコストが安いので、「右から $i+1$ までは既に覆われている」という前提のもとでは完全に上位互換になっているからです。

※もしDPを左から回すと、ここで「遠くまでカバーするものほどコストが高い」という状態になり、1つに確定できません。

結局 $dp\lbrack i+1 \rbrack$ からの遷移は、

単独回線を使い $dp\lbrack i \rbrack$ に遷移する。
部屋 $i$ をカバー範囲に含むルーターのうち最も左のものを使い、その左端を $l$ として $dp\lbrack l \rbrack$ に一気に遷移する。

2つだけを考えれば十分です。これで全体 $O(n)$ でのDPができます。

このDPでは選ばなかったルーター区間について遷移を飛ばしてしまうため、厳密には各点において「整数点 $i, ..., N$ が全て覆われるための最小コスト」になっていません。そのため正当性が少し理解しづらいのですが、各ステップで他と比べて必ず損をするものを切り捨てているので最終的には正しい答えが得られます。

ACコード3

Submission #61186578 - Codeforces

2019-09-22

Codeforces Round #587 (Div. 3) E2. Numerical Sequence (hard version)

Codeforces プログラミング競技プログラミング

Problem - E2 - Codeforces

問題概要

正整数 $x$ に対して、 $1, 2, .., x$ を十進表記で書いたものをこの順に連結した文字列を $s(x)$ とする。例えば $s(11) =$ "1234567891011" である。

そして、 $s(1), s(2), ...$ をこの順に連結した無限の長さの文字列を考える。与えられる $q$ 個の整数 $k_{i}$ に対して、この文字列の $k_{i}$ 番目の文字を答えよ。

制約

$1 \le q \le 500$
$1 \le k_{i} \le 10^{18}$

解法

各クエリに対する $k_{i}$ を単に $k$ と記します。また、問題概要に記したように文字列 $s(x)$ を定めます。

まず、 $k$ 番目の文字がどの $s(x)$ に属するか調べる必要があります。これは $s(1), s(2), ..., s(x)$ の長さの合計を $S(x)$ とすると、 $S(x) \ge k$ を満たす最小の $x$ として求められるので二分探索できます。判定問題を解くために、ある固定した値 $x$ に対する $S(x)$ の効率的な求め方を考えましょう。

$x$ の桁数を $D$ として、 $1 \le d \le D$ なる桁数 $d$ を考えます。整数 $1, ..., x$ に含まれる $d$ 桁の値を抜き出します。この最小値、最大値、値の個数をそれぞれ $m_{d}, M_{d}, n_{d}$ と書くことにすると、これらは以下のように計算できます。

$m_{d} = 10^{d-1}$
$M_{d} = \min(10^{d}-1, x)$
$n_{d} = M_{d} - m_{d} + 1$

やりたいことは文字列 $s(m_{d}), ..., s(M_{d})$ の長さ合計を求めることです。これを $1 \le d \le D$ について合計したものが $S(x)$ になります。

ある $d$ についての計算を、さらに分けて考えます。 $1 \le e \le d$ なる桁数 $e$ について、文字列 $s(m_{d}), ..., s(M_{d})$ の中に $e$ 桁の整数が合計でいくつ入っているかを求めます。

$e \lt d$ のとき、 $s(m_{d}), ..., s(M_{d})$ それぞれに $e$ 桁の整数全てが1つずつ含まれています。 $e$ 桁の整数は全部で $9\times 10^{e-1}$ 種類あるので、合計で $9\times 10^{e-1} \times n_{d}$ 個の整数があります。
$e = d$ のとき、 $e$ 桁の整数は $s(m_{d})$ に1個、 $s(m_{d}+1)$ に2個、...、 $s(M_{d})$ に $n_{d}$ 個含まれています。つまり等差数列の公式から、合計で $\frac{1}{2}n_{d}(n_{d}+1)$ 個の整数があります。

これに $e$ を掛けたものを全ての $1 \le e \le d$ について合計すると $s(m_{d}), ..., s(M_{d})$ の長さ合計が求められます。それをさらに $1 \le d \le D$ について合計したものが $S(x)$ になります。

これを用いて二分探索することで、 $k$ 番目の文字がどの $s(x)$ に属するか求められました。ここで求められた値を引き続き $x$ と記します。ここで $k^{\prime} = k - S(x-1)$ とすると、求めたいのは $s(x)$ の $k^{\prime}$ 番目の文字です。

ここで知りたいのは $s(x)$ として並べられた整数 $1, 2, ..., x$ のうちどれに $k^{\prime}$ 番目の文字が含まれているかで、これはまたしても二分探索することで求められます。つまり $k^{\prime}$ 番目の文字を含むのは、 $|s(y)| \ge k^{\prime}$ を満たす最小の $y$ です。

$|s(y)|$ の計算方法は先ほどの $S(x)$ に比べると簡単で、 $1, ..., y$ の中に $d$ 桁の数がいくつ含まれるかを同じように計算し、それに $d$ を掛けたものを全て合計すれば良いです。

これで $y$ も特定できれば、その十進表記における $k^{\prime} - |s(y-1)|$ 番目の数字が求める文字です。

ACコード

Submission #61031718 - Codeforces

計算量ですが、 $q$ が小さいので10の冪乗などの前計算などをしておかなくても余裕があります。二分探索・桁数 $d, e$ の全探索・10の冪乗で $O(\log k)$ が4つくらい付いていると思います。

またオーバーフローに注意する必要があります。二分探索の初期値としてあまり大きな値を取りすぎると $S(x)$ の値がオーバーフローしますが、実際に計算すると $S(10^{9})$ がだいたい $4.39 \times 10^{18}$ になって $k$ の制約を超えるので、 $x$ の上側の初期値を $10^{9}$ としておくと良いでしょう。

2019-09-22

AtCoder Grand Contest 038 B - Sorting a Segment

AtCoder プログラミング競技プログラミング

B - Sorting a Segment

公式解説と少し違う方法で解いたので記録。

解法

ある長さ $K$ の区間を昇順に並び替えた時に、値が変更される最左のインデックスを $l$ 、最右のインデックスを $r$ とします。この時操作の結果は、閉区間 $\lbrack l, r \rbrack$ 内の要素を昇順に並び替えたものとなります。つまりこの区間 $\lbrack l, r \rbrack$ は「操作によって実質的に並び替えられたのはどの区間か」というものを表します。

f:id:betrue12:20190922003715p:plain

求めたい答えは、 $N-K+1$ 通りの全ての操作パターンについてこのようなインデックスの組 $\lbrace l, r \rbrace$ を求めた時の、それらの相異なる要素数となります。ただし1つも要素が変更されない場合もあるので、その場合は適当に $\lbrace l, r \rbrace = \lbrace -1, -1 \rbrace$ などとしておきます。（開区間と紛らわしいので値の組は $\lbrace \cdot, \cdot \rbrace$ と表記します）

では各操作パターンについて、長さ $K$ の区間 $\lbrack i, i+K-1\rbrack$ を操作したときの $l, r$ はどのように求めれば良いでしょうか。左右同様の方法で求められるので $l$ について考えます。

左端から見て、要素が変更されていない区間 $\lbrack i, l-1\rbrack$ に注目します。この区間に属する全ての値 $j\in \lbrack i, l-1\rbrack$ が満たすべき条件は、 $P_{j}$ より小さい要素が区間 $\lbrack j, i+K-1\rbrack$ に存在しないことです。