Mujin Programming Challenge 2018 参加記録

Mujin Programming Challenge 2018 - AtCoder

結果は3完18分台で274位でした。Cまでは順調でしたが、Dでハマり、Eに切り替えて方針は見えたものの実装を詰めきれず…という感じでした。

f:id:betrue12:20180805003007p:plain

A～Eを振り返っていきます。

A - コンテスト名

先頭5文字を何らかの方法で取ってきて比較します。解説放送でも触れられていましたが、与えられる文字列が短い時に範囲外参照しないよう注意しましょう。言語や書き方によりますが、Rubyの str[s, length] は数が足りなくても取れるだけ取ってくれるので大丈夫です。

ACコード：Submission #2941689 - Mujin Programming Challenge 2018

B - セキュリティ

Mujin Programming Challenge 2018 - AtCoder

文字列を前から見ていって、数字を増やしたり減らしたりします。サンプル3は優しさですね（ありがとうございます）

Submission #2942354 - Mujin Programming Challenge 2018

C - 右折

最初、RPGの氷の床みたいに障害物に当たるまで進み続けるものと思ってました…問題はよく読みましょう。

この問題は、「曲がり角」となる点を固定して考えるとよいです。

f:id:betrue12:20180805005519p:plain

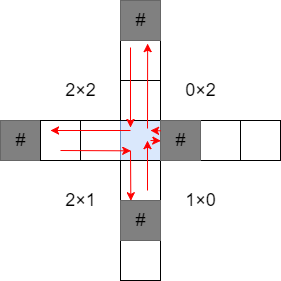
曲がり角を固定すると、例えば「左側からその点まで来て、曲がって下側に行く」という経路は、「障害物を挟まずに、その点の左にいくつマスがあるか」と、「同じく、下にいくつマスがあるか」の掛け算で計算できます。

これを4通りの方向について足せばよいため、

$(左 \times 下) + (下 \times 右) + (右 \times 上) + (上 \times 左) = (左 + 右) \times (上 + 下)$

で「その点を曲がり角とする経路」が求められます。

では、各点について「上下左右に、障害物を挟まずにいくつマスがあるか？」はどのようにして求めましょうか。これを求める良い方法があります。

f:id:betrue12:20180805010831p:plain

図では「左にいくつマスがあるか」を考えています。左に障害物や外壁（範囲外の領域）がある場合はもちろんゼロです。そうでない場合は、左のマスの「左にいくつマスがあるか」の値に1を足したものになるはずです。ということは、左から順にこの数を更新していけばよいです。

上下左右それぞれについてこの方法を使えば、先程の

$(左 \times 下) + (下 \times 右) + (右 \times 上) + (上 \times 左) = (左 + 右) \times (上 + 下)$

の計算ができるため、問題が解けます。前計算、曲がり角の全探索、ともに $O(NM)$ です。

ACコード：Submission #2943455 - Mujin Programming Challenge 2018

制約と解法を認識した瞬間にC++に切り替えたのが功を奏しました。

同じような考え方ができる問題を紹介します。

D - うほょじご

すごく「Snuke Numbers」っぽさを感じたので、初手実験！と思って法則性を探そうとして、失敗しました…

この問題は「整数の遷移をグラフとして考える」というパターンを思い出すべきでした。整数のペアを頂点として考え、遷移に対応する辺を張り、「閉路に到達する」か「 $(0, x)$ または $(x, 0)$ に到達してしまう」かを調べればよいです。

閉路検出しようとしても、書き方が良くないとTLEするのですが…公式解説の「到達してはいけない点である $(0, x)$ および $(x, 0)$ から逆辺を辿る」というのがすごいです。

ACコード：Submission #2946353 - Mujin Programming Challenge 2018

Rubyコードではペア $(i, j)$ に対応する頂点を番号 $i \times 1000 + j$ として扱っています。これを配列で扱うと実行時間がキツいです…。

是非とも英語対応のratedコンテストに出して、タイトルを英訳して欲しかった…と思いましたが、よく考えたらratedでこの問題は見たくなかったですね。良かった良かった（よくない）

E - 迷路

各時刻を $K$ で割った余りごとに、移動できる方向が異なります。これは言い換えると、「現在時刻を $K$ で割った余りに依存して、次に上下左右それぞれの方向に移動するためにかかる時間が変動する」ということです。

まずはこれを求めておきましょう。各時刻において、例えば次に上方向に移動できるのは、文字列 $d$ においてその時刻を $K$ で割った余り以降で、最初に U が登場するような時刻です。これは文字列 $d$ を後ろから見ていって、最後に U が現れてから何文字通過したかを記録していけばよいです。…これ、先程のC問題と考え方は同じですね。

このとき余りがループするのを考慮して、文字列 d を2周すると実装が楽です。

f:id:betrue12:20180805023420p:plain

これを4方向全てについて求めておきます。前計算部分は $O(K)$ です。

その後、実際に目的地に到達する最短時間を求めていくわけですが…遷移ルールが少し特殊とはいえ、過去に遷移することはできません。ということは、スタート地点からの到達時間が短いマスから順に遷移を確認していけば、効率的に各マスへの最短時間を求められそうです。これはまさに、ダイクストラ法の考え方です。

遷移にかかる時間（辺のコスト）が可変であるため普通のダイクストラ法には当てはまりませんが*1、ダイクストラ法における距離の更新は

コスト $c$ の辺 $v \rightarrow u$ を使った距離の更新を考えるとき、始点から $v$ までの最短距離 $dist(v)$ を使って、 $dist(u) = \min(dist(u), dist(v) + c)$ と更新する。

であるため、今回はこれを発展させて次のように考えればよいです。

遷移 $v \rightarrow u$ を使った最短時間の更新を考えるとき、始点から $v$ までの最短時間 $dist(v)$ と、それを $K$ で割った余り $r$ を使う。 $v \rightarrow u$ が上下左右どちらの方向であるかと余り $r$ の値が分かれば、次の移動にかかる時間は前計算しているため、その値を $c$ として $dist(u) = \min(dist(u), dist(v) + c)$ と更新する。

優先度付きキューを用いるとダイクストラ法の計算量は頂点数 $V$ 辺数 $E$ として $O(V \log E)$ であり、今回の問題だと頂点数が $NM$ で辺数は頂点数の4倍で抑えられるので $O(NM \log(NM))$ です。あとは「障害物や外壁の方向には遷移できない」というのを忘れずに実装しましょう。