2018-09-02

ARC102 参加記録

AtCoder プログラミング競技プログラミング

今回も前回に引き続きD問題が700点という、ABCには厳しい回でした…

結果は3完79分で30位…一気に黄色になりました！びっくりですね。highestパフォ400くらい更新しました。

f:id:betrue12:20180902001717p:plain

黄色になりました記事は別途書きます。この記事ではC～E問題を振り返っていきます。

C - Triangular Relationship

解法

$a, b, c$ について、 $a+b, b+c, c+a$ が全て $K$ の倍数でなければいけません。数値が3つあると考えにくいので、まずは1つにできないか考えましょう。

$a+b, b+c, c+a$ から $a$ だけの式を作ることを考えます。 $(a+b) - (b+c) + (c+a)$ を計算すると結果は $2a$ になって、 $a$ だけの式になります。

この値は $K$ の倍数3つを足し引きしているものなので、やっぱり $K$ の倍数です。つまり、 $2a$ が $K$ の倍数であるということが言えます。ここから、

$K$ が偶数の場合、 $a$ は $K$ で割った余りが $0$ または $\frac{K}{2}$ でないといけない
$K$ が奇数の場合、 $a$ は $K$ で割ったあまりが $0$ でないといけない

ということが言えます。

これで、 $a$ を $K$ で割った余りは2通りまたは1通りに絞れました。 $0$ か $\frac{K}{2}$ かで場合分けをして、 $b, c$ も含めて問題の要求を満たす条件を明らかにしていきましょう。

をで割った余りがの時…
- $(a+b)$ が $K$ の倍数であるためには、 $b$ を $K$ で割った余りも $0$ である必要がある。
- 同様に $(c+a)$ が $K$ の倍数であるためには、 $c$ を $K$ で割った余りも $0$ である必要がある。
- $b$ も $c$ も $K$ で割った余りが $0$ であれば、 $(b+c)$ も $K$ の倍数となる。
をで割った余りがの時…
- $(a+b)$ が $K$ の倍数であるためには、 $b$ を $K$ で割った余りも $\frac{K}{2}$ である必要がある。
- 同様に $(c+a)$ が $K$ の倍数であるためには、 $c$ を $K$ で割った余りも $\frac{K}{2}$ である必要がある。
- $b$ も $c$ も $K$ で割った余りが $\frac{K}{2}$ であれば、 $(b+c)$ も $K$ の倍数となる。

書いてあることはほとんど同じになりますね。どちらの場合も、全ての数が共通の余りを持っている必要があります。ここから、以下のように解くことができます。

$N$ 以下の正の整数で $K$ で割った余りが $0$ になるものの数を数え、3乗する。
$K$ が偶数の場合は、 $N$ 以下の正の整数で $K$ で割った余りが $\frac{K}{2}$ になるものの数を数えて3乗し、↑と加算する。

これで解けます。

ACコード

D - All Your Paths are Different Lengths

解法

俗に「構築」と呼ばれる、条件に満たす数列やグラフなどを何か1つ作れという問題。こういう問題では、サンプルの出力例はあまり期待しないほうがよくて*1、制約内の入力のうち何がきても、機械的に同じ手順で対応できるような「必勝法」を探すことが多いです。

さて、最も主要な条件は「頂点 $1$ から頂点 $N$ までの経路が $L$ 通りあって、それらの長さが $0, ..., L-1$ になっている」ということです。このように連続する自然数をもれなくダブりなく表現する方法として、10進数や2進数のような進数表記があります。

とりあえず2進数で考えてみます。そして、まずはキリ良く $2^{N-1}$ 通りの数を表すことを考えてみましょう。

f:id:betrue12:20180902013420p:plain

このように $N$ 頂点のグラフを作ってみると、左端から右端までの経路は「4回の移動でそれぞれ上下どちらを通るか？」の組み合わせで $2^{4} = 16$ 通りです。そしてこれで、長さ $0, ..., 15$ のパターンを綺麗に網羅しています。もし $L$ が $2^{N-1}$ の形で表せるような数だったら、これが答えになりますね。

これを基本アイデアとして、端数を調整していくことを考えましょう。例えば $L = 20$ の場合は、長さ $0, ..., 15$ を作った後、そこに長さ $16, 17, 18, 19$ の経路を追加する必要があります。この経路は以下のように追加することができます。

f:id:betrue12:20180902014617p:plain

$L = 22$ の場合はどうでしょうか。追加したい経路が6個なので一度に追加することは難しいですが、 4+2と分ければ以下のように追加することができます。

f:id:betrue12:20180902014709p:plain

一般的に考えると、2進数で作った経路の途中までを見ると $2^{k}$ の経路ができていて、その長さが $0, ..., 2^{k}-1$ になっているはずです。そこから適切な長さでゴール地点までのショートカットを作ると、好きな数字から始まる $2^{k}$ の連番が作れますね。これを良い感じに組み合わせていくと、作りたい長さまでの連番ができます。

最後に、頂点数と辺数について確認しておきます。*2

頂点数 $N \le 20$ だと2進数の桁を最大19個作ることができて、2進数19桁で表現できる数は $2^{19}$ 通りです。そこからショートカットを $N$ 以外の全頂点から追加で1本ずつ伸ばすと、増える経路数はそれぞれ $+2^{18}, +2^{17}, ..., 1$ であり、最大で $2^{20} - 1 = 1048575$ 通りになります。 $L \le 10^{6}$ （100万）なので頂点数は足りそうです。

辺数 $M \le 60$ については、まず2進数19桁を作るのに38本。ショートカットを1本ずつ伸ばすと、追加が最大19本で合計57本。足りそうですね。

ACコード

E - Stop. Otherwise...

解法

※実は要らないらしいのですが包除で解いたので包除で解説を書きます。

基礎知識

まず今回の問題を解くには、「 $K$ 個のものから、重複を許して計 $N$ 個選ぶ時の組み合わせ」の数え方が必要です。*3

これは重複組合せと呼ばれていて、 $_{K}H_{N}$ と記載することもあります。その総数は公式として有名で、通常の組み合わせの記号を使うと $_{K+N-1}C_{N}$ 通りとなります。

あとは包除原理。一般には、「または」の計算を「かつ」の結果の足し算引き算だけで求めることができるという原理です。

そのまま使うこともありますし、問題では「どの～も○○でない」という「かつ」型の条件が与えられていて、そのままだと考えにくいので条件を反転して「または」型の条件にしてから包除原理を使うこともあります。今回の問題はそのタイプです。

考察

どの2つのサイコロの和も $i$ にならない、という条件をいくつか書き下してみましょう。

和が2にならない。
- 1と1の組み合わせが作れない。つまり、1の数が0～1個。
和が3にならない。
- 1と2の組み合わせが作れない。つまり、1と2の少なくとも片方が0個。
和が4にならない。
- 2の数が0個～1個。
- 1と3の少なくとも片方が0個。
和が5にならない。
- 1と4の少なくとも片方が0個。
- 2と3の少なくとも片方が0個。

こんな感じになります。

これを一般化してみると、 $i$ それぞれについて、問題の要求は以下のような条件になります。

同一数のペアによる条件（が偶数のときのみ）
- ある1つの出目 $\frac{i}{2}$ について、その個数は0～1個である。
異なる数のペアによる条件
- ある $M$ 個の出目のペアについて、そのうち少なくとも片方は0個である。

（これらの数やペアには、重複して含まれる出目がない、ということも大事です。）

少なくとも片方が0個である必要がある、揃ってはいけないペアのことを「NGペア」と書くことにします。それぞれの $i$ についてのNGペアの個数 $M$ は、面数 $K=6$ とかで書き下してみるとなんとなく法則が分かると思います。

$i$ が奇数の場合のほうが条件が少ないので、まずは奇数の場合を考えます。

$i$ が奇数の場合

「 $M$ 個のNGペアのうち $m$ 個を固定した時、それらが全て存在しているような場合の数」というのを考えます。残りのペアについては、存在しているかどうかは不問です。これを全ての $m$ について求めると、包除原理でNGペアが0個の時の場合の数が求められます。

この固定したペアの出目は必ず存在するので、まず出目にサイコロを1個ずつ割り当てます。残ったサイコロは $N - 2m$ 個です。

最後に、残ったサイコロは $1, ..., K$ のどの目になってもよいので、 $K$ 個の出目から $N-2m$ 個を選ぶ重複組合せを数えます。この過程で、新しいNGペアができたり、固定したNGペアがさらに増えたり、NGペアが全く増えなかったりしますが、これらは分けて考える必要がありません。これはとても便利で、包除原理を使ってまで条件を言い換える最大のメリットになります。

f:id:betrue12:20180902024230p:plain

このように計算すると、「 $M$ 個のNGペアのうち $m$ 個を固定した時、それらが両方存在しているような場合の数」は $_{K}H_{N-2m}$ です。

$m$ 個のペアの選び方は $_{M}C_{m}$ 通りなので、これらをまとめると

$_{M}C_{m} \times _{K}H_{N-2m}$

となり、この値を包除原理に基づいて足し引きしていけば、答えが求められます。

$i$ が偶数の場合

$i$ が偶数の場合は同一数のペアによる条件があって、具体的には出目が $\frac{i}{2}$ のサイコロの個数が0～1個でなければいけません。

というわけで、0個か1個かで場合分けをします。同一数のペアによる条件を処理してしまえば、あとは奇数の場合と同じように考えることができます。出目が1つ使えなくなることに注意してください。

出目がのサイコロが0個の場合
- サイコロの出目の総数が $K-1$ 個、サイコロが $N$ 個として、奇数の場合と同様に考えられる。
出目がのサイコロが1個の場合
- サイコロの出目の総数が $K-1$ 個、サイコロが $N-1$ 個として、奇数の場合と同様に考えられる。

これを両方計算して、合計すればよいです。

ACコード

（C++）Submission #3118700 - AtCoder Regular Contest 102

さいごに

700点問題が本番で通るようになってきたのは本当に嬉しいです。実際、500～800点くらいの過去問をけっこう解いてきたので、その成果が出ていると思います。

次の記事は「AtCoder黄色になりました」の予定です！

脚注

*1:本来の解法を隠すために、わざと不規則な例になっていることも多いです。

*2:今回は説明の流れを切らないために、最後に制約確認をしましたが、実際にはアイデアの骨子が浮かんだ段階で「足りそうか？」というのを考えるほうが良いとは思います。これで足りない場合、2進数から別のn進数に考え直してみるか、節約の方法を考えるか、全く別のアプローチを考えるか、になると思います。

*3:今回の問題と記号を合わせています。リンク先のWikipediaと逆なので注意。

2018-08-26

Summer Festival Contest 2018 参加記録

AtCoder プログラミング競技プログラミング

Summer Festival Contest 2018 (Division 1) - AtCoder

結果は2完で7位でした。D問題の最速ACも取れちゃいました。

f:id:betrue12:20180826135558p:plain

DとEを振り返ります。

D - 木からパスへ (Tree--->path)

解法

問題の操作は、以下のように考えることができます。

与えられた木の辺を切断して、頂点を共有しないいくつかのパスに分解する。頂点は全てどこかのパスに含まれる。孤立した頂点（1頂点0辺の集合）もパスとみなす。
与えられたパス群を、パス数-1個の頂点を追加することで連結させる。

そのため、1. のパス分解において、なるべく少ない個数のパスに分解する方法を考えます。

何となく、長いパスで多くの頂点を巻き込んだほうが得なようにも見えますが、それは正しくありません。極端な例を挙げます。

f:id:betrue12:20180826141627p:plain

図のように、なるべく近いところでパスを作っていくほうが、他のパスを邪魔しなくてよいです。

このようにパスを作っていくため、与えられた木を根付き木として考えます。なるべく深いところ同士でパスを完結させてしまおう、という考えです。木DPのように深いところから見ていって、以下のようにパスを作っていきます。

f:id:betrue12:20180826143125p:plain

これを最深部から根まで行えば、全頂点を網羅するパスができているはずです。作られたパスの数-1が答えです。

ACコード

（C++）Submission #3069309 - Summer Festival Contest 2018 (Division 1)

E - 石積み (Pyramid Piling)

解法

この問題はまず「長さ $s$ の $n$ 次元三角数がどんな値になるか？」を把握する必要があります。2次元の $\frac{s(s+1)}{2}$ 、3次元の $\frac{s(s+1)(s+2)}{6}$ あたりが知識としてあると、 $\frac{s(s+1)\cdots(s+n-1)}{n!}$ あたりになりそうだなあ…という予測は立ちますが、ちゃんと考えます。

問題文の定義より、「 $x_{i} \ge 0$ かつ $x_{1} + ... + x_{n} \lt s$ が成り立つ整数 $(x_{1}, ..., x_{n})$ の組」の数を考えます。これは「マルと仕切りを並べる順列」で考えることができます。

f:id:betrue12:20180826152122p:plain

上記の考え方により、条件を満たす整数の組は $_{n+s-1}C_{n}$ 通りです。これは先ほどの予測の式と一致しています。

三角数の一般式が得られたところで、問題を解いていきましょう。求めたい解は、

$\frac{s_{1}\cdots(s_{1}+N-1)}{N!} = \frac{s_{2}\cdots(s_{2}+N-2)}{(N-1)!}$

を満たす $s_{1}, s_{2}$ であり、分母を払うと

$s_{1}\cdots(s_{1}+N-1) = s_{2}\cdots(s_{2}+N-2) \times N$

となります。左辺は連続する整数 $N-1$ 個の積、右辺は連続する整数 $N-2$ 個の積 $\times N$ です。要素数が同じなので、上手く対応付けられそうです。

$s_{1} = N$
$s_{1} + 1 = s_{2}$
...
$s_{1} + N - 1 = s_{2} + N -2$

を満たすように対応付けられれば良くて、これを満たすものは $s_{1} = N, s_{2} = N+1$ となります。これは解として正当です。

※ $s_{1} = s_{2} = 1$ も式を満たすのですが、問題で $s_{1} \ne s_{2}$ が要求されているのでこれはNGです。

ACコード

（Ruby）Submission #3069695 - Summer Festival Contest 2018 (Division 1)

なお私の場合、すぐこの解にたどり着いたわけではなく、一度地道に探索するコードを書いて、その結果から規則性に気付いています。地道コードのほうもせっかくなので提出してリンクを貼っておきます。小さい入力値でしか動かないので当然ACにはならないのですが、このようなコードを一度書いて実行してみると気付きが得られるかもしれません。

2018-08-26

ARC101 参加記録

AtCoder プログラミング競技プログラミング

水色以上の人にとっては実に1ヶ月以上ぶりのratedコンテストとなりました。そのぶん気合十分、緊張も十分の状態で臨みましたが…

結果は74分台2完で139位。700点問題を解くことができて、レートも結構上がりました。

f:id:betrue12:20180826004211p:plain

CとDを振り返っていきます。

C - Candles

解法

ろうそくの消し方は、初期位置（座標0）とろうそくの位置関係によって以下の3パターンに分かれます。

ろうそくが全部左（0以下）にある。一番左のろうそくまでの片道距離がかかる。
ろうそくが全部右（0以上）にある。一番右のろうそくまでの片道距離がかかる。
ろうそくが左右どちらにもある。途中でUターンが必要であり、左右端のうち短いほうへの往復距離と長いほうへの片道距離がかかる。

これらどのパターンにおいても、「連続しないろうそくをわざわざ選ぶ」ことで得になることはないです。イメージとしては、できるだけ密集しているろうそくを選んだほうが得な気がしますよね。

$N$ 個のろうそくから連続する $K$ 個のろうそくを選ぶ選び方は $N - K + 1$ 通り。距離計算に使うのは両端だけなので、1パターンごとの計算は $O(1)$ でできます。全パターン探索しても全体計算量は $O(N)$ 、 $N \le 10^{5}$ なので間に合います。

ACコード

D - Median of Medians

恐怖の700点問題。これはABCに出すには流石に無理がありますね…ただ、知っておいて損はない問題だとは思います。

長さ $N$ の数列の連続部分列のとり方は $\frac{N(N+1)}{2}$ 通りありますが、それら全ての中央値を集めて、さらにその中央値を求める問題。要素数がとても多くなるので、直接求めるのは難しそうです。ちょっと細かく考察を書いていきます。

中央値について考察

「中央値」というのは、要素の個数に直接関係する概念です。例えば

$1, 2, 3, 4, 5, 6, 7$

という数列の中央値は4ですが、これは「4以上の要素が半数以上存在する」ということを意味します。

ただ、もちろん1や2についても同様のことが言えますね。「 $X$ 以上の要素が半数以上存在する」を満たす数はたくさんありますが、そのうち最も大きな $X$ が、（この問題上の定義における）中央値です。これは例えば

$1, 4, 4, 4, 4, 4, 5$

のように分布の偏った数列についても同じことが言えます。

平均値と違い、中央値を考える上では「中央値以上かどうか」だけが重要です。

$1, 2, 3, 4, 5, 6, 7$ でも、
$1, 2, 3, 4, 5, 6, 5000兆$ でも、
$1, 2, 3, 4, 5000兆, 5000兆, 5000兆$ でも、

どれも中央値は4です。

Yes/No問題＋二分探索への転換

前項で書いたとおり、「中央値は $X$ 以下である」ことと、「 $X$ 以上の要素が半数以上存在する」ことは同値です。

そして、「整数 $X$ が与えられたとき、集合の要素の中に $X$ 以上の要素は半数以上存在するか？」というYes/No問題は、直接中央値を求める問題よりもずっと考えやすくなります。というのも、各要素の具体的な値は全部無視して、 $X$ 以上かどうか、だけで2値化して考えれば良いからです。

このことから、中央値の二分探索を行うという方針が立ちそうです。具体的には、二分探索の各ステップごとに $X$ を固定して、先ほどのYes/No問題を解き、その結果に応じて範囲を狭めて求める中央値を特定していく…という方法を考えます。*1

区間数え上げの効率化

さて、元の問題は「 $\frac{N(N+1)}{2}$ 個の連続部分列の中央値 $\frac{N(N+1)}{2}$ 個を集めた集合の中央値を求めよ」でした。

Yes/No問題に切り替えた後は、 $\frac{N(N+1)}{2}$ 個の区間のうち、区間内の要素の中央値が $X$ 以上となるような区間の数を数えるのが次の目標になります。そのような区間は、やはり中央値の性質から「区間内に $X$ 以上の要素が半数以上あるような区間」と言い換えることができます。

これを全ての区間について直接計算すると結局 $O(N^{2})$ 以上の時間がかかって間に合わないので、効率化のため累積和を使います。 $X$ 以上の要素を+1、 $X$ 未満の要素を-1として累積和を取った時、区間和が0以上であるものが「区間内に $X$ 以上の要素が半数以上あるような区間」です。

このように累積和を用いて、区間和がある条件を満たす区間を数え上げる問題はお馴染みです。ただ例えば「区間和がぴったり0」などの条件でしたら*2単純にmapなどで個数管理すればよいのですが、今回は「以上」なので範囲和が必要になります。そのため、BIT（Binary Indexed Tree）などを使うことになります。

f:id:betrue12:20180826115439p:plain

BITについては、蟻本の解説、もしくは以下のスライドがオススメです。

http://hos.ac/slides/20140319_bit.pdf

解法まとめ

これで問題を解く全ての材料が揃いました。手順としては、

二分探索を試みる。各ステップでは $X$ を固定し、「 $\frac{N(N+1)}{2}$ 個の中央値の中に $X$ 以上のものは半数以上存在するか？」のYes/No問題を考える。
与えられた数列の、 $X$ 以上の要素を+1、 $X$ 未満の要素を-1として累積和を取り、区間和が0以上になる区間をBITを利用して数え上げる。この合計が、 $\frac{N(N+1)}{2}$ 個の中央値の中に存在する $X$ 以上の要素数となる。
数え上げ結果によってYes/No問題が解かれるので、これを繰り返して二分探索の範囲を狭め、解となる中央値を特定する。

となります。

何と言ってもABCに出たので凶悪難易度に見えますが、700点問題として見ると適正なのかな…と思います。

ACコード

（C++） Submission #3077246 - AtCoder Regular Contest 101

実装上の細かい話ですが、BITは普通は負のインデックスに値を格納できないので、適当にオフセットを付けてやる必要があります。上のコードは0-indexedのBITなので +N してますが、1-indexedのBITだと0を格納しようとしてバグる危険性がちょっとだけあるので、不安なら長さを多めにとって +N+1 しましょう。

また、二分探索は制約範囲内の整数全部を考えても良いのですが、「元の数列に存在する要素のどれかしか中央値になり得ない」ということから、元の数列の要素をソートして候補として使っても良いです。上のコードはそうしています。反復回数がちょっと少なくなると思います。

さいごに

過去にABCで出た700点問題は「考察キツいけど数学で解ける」だったり「考察キツいけどDijkstraで解ける」だったりしたのですが、今回は考察もキツめでBITも必要だったことを考えるとかなり厳しかったのではないかと思います。ARCでもこれが解ければ最遅でも黃パフォだったので、そのくらいのレベルです。

私はこのくらいの難易度の問題を安定させられるようになりつつ、全く歯が立たなかった900点問題に少しでも手がかかるようにしたいな…と思います。ちょっと黄色が見えてきた気がするので、引き続き頑張ります。

脚注

*1:「中央値は二分探索と相性が良い」というのは、競プロ的には知識として持っておくと役立つと思います。ただその理由である、「中央値がX以下であるか」問題に転換すると要素を2値化できるので解きやすい、というところまで合わせて理解しておくほうがいいと思います。

*2:有名なZero-Sum Rangesなど

2018-08-20

Codeforces Round #505 参加記録

Codeforces プログラミング競技プログラミング

Dashboard - Codeforces Round #505 (rated, Div. 1 + Div. 2, based on VK Cup 2018 Final) - Codeforces

3完で541位。Div1+Div2混合回でこの順位なので、レートもそこそこ上がりました。

f:id:betrue12:20180820193230p:plain

BもCも解くのが遅めだったんですが、この回はとにかくプレテストが弱い問題が多くて…大量のシステス落ちが発生した結果、生き残った私の順位が上がった感じです。

3問振り返っていきます。

A. Doggo Recoloring

Problem - A - Codeforces

文字列 $s$ に以下の操作を任意回数行うことで、全部同じ文字にすることができますか、という問題。

文字列中に2つ以上存在する文字を選び、その文字を好きな文字に置き換える。

もし2つ以上存在する文字が1種類でもあれば、 aabc → bbbc → cccc のように、他の文字を全部拾っていくことができます。また、文字列が2文字以上で かつ全部の文字が異なる場合は、1度も操作を行えません。

文字列が1文字の時は何もしなくても条件を満たしているので、そこだけ注意です。

ACコード（Ruby）：Submission #41830470 - Codeforces

B. Weakened Common Divisor

Problem - B - Codeforces

$n$ 個の整数ペアのリスト $(a_{1}, b_{1}), ..., (a_{n}, b_{n})$ が与えられます。このペア全てに対して「 $a_{i}$ または $b_{i}$ は $p$ で割り切れる」を満たす2以上の整数 $p$ を、このペアリストのWCDと呼ぶことにします。与えられたペアリストのWCDを1つ示すか、WCDが存在しないことを判定しなさいという問題。

$n \le 10^{6}$ 、 $A = \max(a_{i}, b_{i})$ として $A \le 2 \times 10^{9}$ と制約がやや大きめです。WCDを1つだけ示せばいいので素数だけに絞っていいことは分かりますが、「全部の入力を素因数分解する（ $O(n\sqrt{A})$ ）」や「解になり得る全素数を試す（ $O(n\frac{A}{\log A})$ ）*1」などは間に合いません。

どれか1つのペア、例えば $(a_{1}, b_{1})$ に注目します。探す範囲を素数に絞ると、解の候補は $(a_{1}, b_{1})$ どちらかの素因数であるはずです。全部の入力を素因数分解するのは大変ですが、2つくらいなら $O(\sqrt{A})$ で余裕です。また、ここで得られる素因数は多くても15個くらいになります*2。

ここで得られた解の候補（高々15個）を、残りの入力ペアでひたすら試して、ふるい落としていけばよいです。 $15 \times 2 \times 10^{6}$ 回ほどの剰余算になりますが、これくらいなら間に合います。

ACコード（C++）：Submission #41899593 - Codeforces

本番コードもそんなに差はないんですが、素因数列挙のライブラリが謎な感じだったので出し直し…

C. Plasticine zebra

Problem - C - Codeforces

w と b で構成される文字列 $s$ に以下の操作を任意回数行って、 wbwbw のように1文字ずつ交互に現れるような連続部分列を最大何文字作れますか、という問題。

文字列を好きなところで2つに分割し、その両方を左右反転する。

「好きなところで分割して両方を左右反転する」という操作がどういうものなのかイメージが付きづらいですが…ちょっと実験してみます。

w と b だと分かりにくいので、番号を付けて s = 123456 とします。まずこれを適当に半分で分割して左右反転し 321654 とします。その後…

3 | 21654 と分割・反転すると、 345612 になる。
32 | 1654 と分割・反転すると、 234561 になる。
3216 | 54 と分割・反転すると、 612345 になる。

このように、元の文字列がローテーションするような文字列になります。

そもそも1回目に分割した後の 321654 も 654321 がローテーションしたものです。問題に答えるにあたっては左右が反転しても関係ないため、結局この問題は、

$s$ の全てのローテーションについて、wbwbw のように1文字ずつ交互に現れるような連続部分列を考えた時、その最大長はいくつか

という問題に帰着できます。

操作結果がローテーションになるというのは、以下のように考えるとイメージしやすいかもしれません。文字列を円周上に並べてみると、問題文の操作は円周内での位置を動かしますが、文字と文字が交差して入れ替わることはありません。

f:id:betrue12:20180820211505p:plain

さて、答えを求めましょう。文字列の長さが $|s| \le 10^{5}$ と大きいので全ローテーションを愚直に調べると間に合いません。私は「同じ文字が連続しているところで切断する」というまどろっこしい実装をしてしまいましたが、「 $s + s$ の連続部分列を調べて、結果が $|s|$ を超えたら $|s|$ にする」という実装が一番シンプルだと思います。

本番コード（C++）：Submission #41843610 - Codeforces
賢いコード（C++）：Codeforces

さいごに

私が全く解けなかったD問題もプレテスト段階では1000人くらい通していたのに、システスで残ったのは500人くらい。本当に波乱の回でした…前日・前々日と連続でシステス落ちした経験が生きたかなと思います。

脚注

*1:素数定理というものがあって、整数A以下の素数の個数を見積もることができます。20億以下の素数の個数はだいたい1億程度です。

*2:素因数をなるべく多く稼ごうと思うと、小さい方から素数を掛けていくことになりますが、素数16個目で積が(2×10⁹)²を超えます。なので16個以上は得られません。

2018-08-19

Educational Codeforces Round 49 参加記録

Codeforces プログラミング競技プログラミング

Dashboard - Educational Codeforces Round 49 (Rated for Div. 2) - Codeforces

前回に続き、今回もシステス落ち…

Aがシステスで落ちてBCDの3完。簡単な問題が落ちるとペナルティが重いです。

f:id:betrue12:20180819181738p:plain

本番中取り組んでいたEも含めて5問振り返っていきます。

A. Palindromic Twist

Problem - A - Codeforces

偶数個のアルファベット小文字からなる文字列 $s$ が与えられます。その文字それぞれに対して、「アルファベットを前か後ろに1つずらす」という操作を必ず1回ずつ行うことで、 $s$ を回文にできるか判定しなさい、という問題。

2個の文字を前か後ろに1つずつずらすことで一致させることできる条件は、「同じ文字であること」「ずらす時の距離が±2であること」のいずれかを満たすことです。整数に変換して差を取ります。

ACコード：Submission #41820490 - Codeforces

本番ではなぜかaとzがループするものだと思っていてコードを書き、システスで落ちました…

B. Numbers on the Chessboard

Problem - B - Codeforces

$n \times n$ の盤面に、以下のように番号が振られています。

まず、座標 $(x, y)$ の和が偶数になる点にだけ、左上から右下に順に番号を振る。このような点の数は $\lceil\frac{n^{2}}{2}\rceil$ 個である。
続けて、残りの点に左上から右下に番号を振る。

与えられた座標に書かれている値を答えなさい、という問題。

ちまちまと計算していけば良いのですが実装が面倒で、特に $n$ が奇数の時が厄介です。コードの方針としては、

座標和が奇数であれば、まず $\lceil\frac{n^{2}}{2}\rceil$ を加算する。これは座標和が偶数のマスに割り当てられている数字の数。これ以降は、座標和の偶奇が自分と同じマスだけ考えればよい。
自分より上にある行を2で割った数 $\times N$ を加算する。座標和が偶数であっても奇数であっても、 $n$ が偶数であっても奇数であっても、隣り合う2行で消費する数字の個数は $N$ であるため。
自分より上にある行数が奇数なら、2. で足されていない1行が余っているので、その個数を加算する。
自分の行で、自分自身とその左にある要素の個数を加算する。

f:id:betrue12:20180819114850p:plain

これを実装し、問題文中にある $4 \times 4$ と $5 \times 5$ の全マスを出力させて正しいことを確認してからsubmitしました…。

ACコード：Submission #41764843 - Codeforces

C. Minimum Value Rectangle

Problem - C - Codeforces

与えられた棒の中から4本使ってできる長方形のうち、周の長さ $P$ 、面積 $S$ として $\frac{P^{2}}{S}$ が最小になるものを見つけなさい、という問題。

まず、辺として使える長さの候補について考えます。長方形を作るには、同じ長さの棒が2ペア必要です。4本あれば正方形が作れます。ソートして前から見るか、map等で各長さの棒の本数を数えていけば列挙できます。

長方形の隣り合う辺の長さを $a, b$ とすると、 $P = 2(a+b), S = ab$ であるため、評価式は $\frac{P^{2}}{S} = \frac{4(a+b)^{2}}{ab}$ となります。この分子・分母の関係は相加・相乗平均の関係に似ていて、 $a = b$ の時16で最小値を取ります。直感的には、 $a, b$ がなるべく近い値であればよさそうです。

そのため、辺として使える候補をソートし、隣り合うものを全部試すことを考えます。隣り合うものを使わない場合は結果が悪くなることが、不等式を使って頑張れば示せます*1。全部試して一番評価式が小さいものを出力します。

独立な複数の問題が1つのテストケースにまとまっているので計算量の評価が難しいですが、それぞれの問題は棒の数 $n$ に対して $O(n \log n)$ （ソートの計算量）で解けて、全問題の棒の数の総和を $N$ とすると $N = \sum n \le 10^{6}$ であることを考えると、 $O(N \log N)$ で全体計算量が抑えられると思います。

まあRubyではTLEしましたが…

ACコード：Submission #41772412 - Codeforces

D. Mouse Hunt

Problem - D - Codeforces

$n$ 個の部屋それぞれにネズミが出没し、各部屋について「その部屋に来たネズミは次にどの部屋に行くか」を示す $a_{i}$ が設定されています（ $a_{i} = i$ の時はその部屋に留まり続けます）。また各部屋に、ネズミ取りを置くためのコスト $c_{i}$ が設定されています。

「どの部屋にネズミが出ても、必ずどこかで捕まえられる」という条件を満たすために必要な最小コストを求めてください、という問題。

ネズミの移動を追っていくと、どの部屋から出発しても最終的には以下のいずれかになります。

$a_{i} = i$ であるいずれかの部屋に留まり続ける。
循環するサイクルになっている複数の部屋を無限に周り続ける。

そのため、この最終地点にネズミ取りを仕掛けるのが効率が良いです。 $a_{i} = i$ である部屋にネズミ取りを仕掛け、サイクルになっている場合はその中で一番コストが安い部屋1つにネズミ取りを仕掛けます。それ以外の部屋からスタートしたネズミも、最終的には必ずこれらのいずれかの部屋に来るため、捕まえられます。

f:id:betrue12:20180819121857p:plain

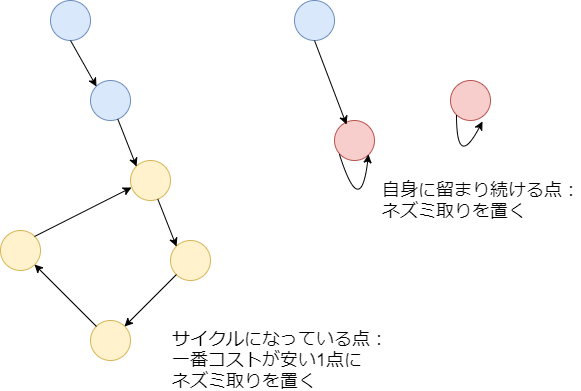
というわけでグラフを作ります。サイクルを潰したいので、ちょっとオーバーキルな気もしますが強連結成分分解を使います。ライブラリ持ってたし。

方針として、

部屋を頂点、ネズミの移動を辺とする有向グラフを作る。
強連結成分分解でサイクルを潰し、「サイクル内の点の中で一番安いコスト」を持つ点とみなす。
サイクルのない有向グラフ（DAG）になったので、移動の終端となる、つまり出次数が0である点のコストを合計する。

これで解けます。

ACコード：Submission #41779227 - Codeforces

E. Inverse Coloring

Problem - E - Codeforces

$n \times n$ の盤面に白または黒のタイルを貼ります。以下の条件を満たすタイルの貼り方を数え上げなさい、という問題。

$i+1$ 行目のタイルの貼り方は、 $i$ 行目と全く同じか、またはそれを白黒反転させたものである。
列についても、同様の条件を満たす。
同じ色のタイルで構成される長方形の面積は $K$ 未満である。*2

長方形の面積は隣り合う2辺を $a, b$ として $a \times b$ なので、「同じ色が横に何連続しているか」「縦に何連続しているか」を気にしながら数え上げていくことを考えます。

f:id:betrue12:20180819143841p:plain

まず、1行目のタイルの貼り方を数え上げます。このとき、「同じ色が横に最大で何連続しているか」ごとに区別して数え上げていきます。この値を $a$ としておきます。

そのタイル1行について、2行目以降は「反転する」「反転しない」の分岐で数えていくことができます…が、「反転しない」を連続で選び続けると縦に同じ色が連続してしまい、面積の条件を破ってしまいます。具体的には反転しない連続回数を $b$ とすると、 $a \times b \lt K$ を満たす範囲に $b$ を収める必要があります。

数え上げ方針が立ったので、DPを考えていきます。1行目の貼り方は、「 $i$ 枚目まで見て、これまでの最大連続回数が $j$ で、今見ているところまでの連続回数が $k$ である貼り方」をテーブルに持って $O(N^{3})$ のDPができます。それを $i=N$ まで見た時の値が、「横に最大で $j$ 連続している1行目のタイルの貼り方」になります（ $k$ の区別はもう要らないので合算しちゃいましょう）。

そこから、「 $i$ 行目まで積んで、横に最大で $j$ 連続していて、今見ているところまでの縦の連続回数が $k$ であるタイルの貼り方」をテーブルに持つDPをします。これも同様に $O(N^{3})$ です。ただし $j \times k \lt K$ を満たさないような値については加算しません。これで答えが求まります*3。

さてこれを実装してサンプルも確認して提出したものの… $501^{3}$ の配列が大きすぎてコンパイルエラー。どのみちコンパイルが通ったとしてもMLEなので、メモリ節約のため2次元配列を使い回すように書き換えると今度はTLE。コンテスト中はそれで終わってしまいましたが、そこからさらに不要なループ範囲を削って定数倍の高速化をすれば通すことができました。