Educational Codeforces Round 58 G. (Zero XOR Subset)-less
お題箱より。
問題概要
長さ の数列
が与えられる。これをいくつかの区間(連続部分列)に分割する。この分割は以下の条件を満たす必要がある。
このような分割が可能であれば最大いくつの区間に分割できるかを求めよ。不可能であれば -1 を出力せよ。
制約
解法
XOR演算を記号 で表すことにします。また「区間和」や「累積和」などの用語は、XORで計算したものを指すことにします。
区間和を考える上では先頭からの累積和を取るのが有用です。まず先頭からの累積和 を計算します。ただし
とします。
ある分割方法が本問題の条件を満たすための必要十分条件を、この累積和を用いて表現することが目標です。例えば以下の図のようにインデックス で4つの連続部分列に区切った分割を考えます。

このときそれぞれの区間和は となります。このうち1つ以上を選んでXORを取ったものが
にならないことが本問題の条件で、これはまさに線形代数における「一次独立性」です。整数を2進数表記して
の要素からなるベクトルと考え、足し算の代わりにXOR演算を用いる、いわゆる
上の線形代数と呼ばれるものを考えます。
この一次独立性は、「ある要素を、別の要素にXORで足す」という操作をしても変わりません(参考)。この性質から、 が一次独立であることは
が一次独立であることと同値です。
より一般的に言えば、インデックス で
個の区間に区切るような分割が本問題の条件を満たすことと、
が一次独立であることは同値です。すなわちこの問題は「累積和
の中から、
を必ず選び、さらに他の要素を0個以上選ぶ。それらは一次独立である必要がある。最大でいくつの要素を選べるか?」という問題に帰着できます。
これは、もし であればどのように選んでも一次独立にできないので
-1 を出力。そうでない場合は掃き出し法によって一次独立な要素の最大個数(=それらを基底として張られる線形空間の次元数)を求めることができます。
先ほど帰着した問題に素直に従うと、 をまず基底に加えて、それから他の要素を追加していく掃き出し法によって解くことができます。ただ実際は、次元数は基底の候補をどの順番で処理するかに依存しないので好きな順番で追加して大丈夫です。
ACコード
AtCoder Beginner Contest 170 F - Pond Skater
解法
1ターンに1マスの移動であればグリッド上のBFSで解けますが、今回は1ターンに マスまで動くことができます。これをそのままBFSで処理すると1つのマスから遷移可能なマスが最大
個になり、全体計算量
になって間に合いません。
具体的にどのように無駄が生じているのかを、マスが一直線に並んでいるケースで見てみます。マス内の数値はスタートからの最短距離です。
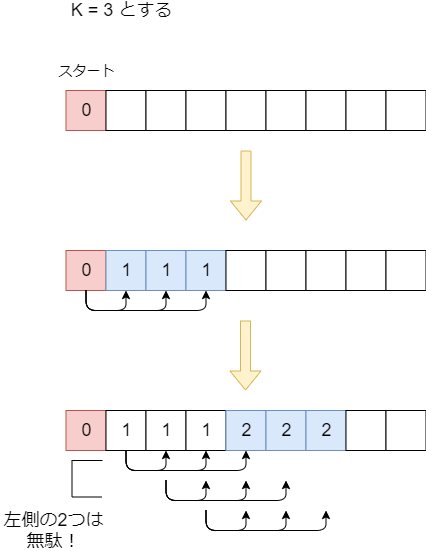
このように、同じターン数で自分より先を行っている経路を後から追うのは無駄です。これを除外するため、BFSに以下のような改良を加えます。
- スタートからマス
までの距離を
として、キュー等を用いたBFSを行う。
- あるマス
からの遷移として、4方向の移動をそれぞれ試す。決めた方向に対して、
マス移動した先を順番に見ていく。
- このとき移動先のマス
が、障害物、枠外、または
であるようなマスだった場合、その方向の遷移をそこで打ち切る。
- その上で、
が未訪問マスであった場合は
としてキューに入れる。
- このとき移動先のマス
このようにすると、先ほどの無駄な移動は打ち切られます。
この解法の正当性確認と計算量評価をしましょう。正当性は、「 であった場合、打ち切らずに
からの遷移を考える代わりに、
からの遷移をすることでより良い遷移ができる」ことから言えます。より良い遷移とは具体的には、より遠くのマスまで届いてかつ
の値が同じかより小さい、という意味です。
計算量については、あるマスに対して遷移で入ってくる回数を考えると分かります。入ってくるけどそこで打ち切られるような場合を除くと、あるマスに入ってくる回数は各方向あたり高々1回ずつです。具体的にはそのマスにある方向から流入可能なマスのうち、 が最も小さく、かつ
が同じものの中では最も近いものからしか流入しません。
よって、方向数 を定数と見なせば「打ち切られ」以外の遷移回数は合計で
。打ち切られる回数の合計も(今度は遷移元に注目すると)マス数×方向数で
です。よって全体計算量
となり間に合います。
ACコード
東京海上日動 プログラミングコンテスト2020 D - Knapsack Queries on a tree
D - Knapsack Queries on a tree
Editorialと同じ解法で解いたのでそっちを書きます。クエリごとに独立に解く方法もあって、そっちで解いた人のほうが多そうな印象です。
解法
が十分大きいという前提で解説をします。また扱う重みの最大値を
、最大深さの半分の値を
とします。(Editorialに合わせています)
本質となる考え方は、以下の図のように深さ 以下の木を上側の
と下側の
に分けることです。

上側をDPで前計算
まず上側については、頂点数が 個です。これらの頂点について、ナップサック問題ではお馴染みの以下のDPを行います。
根から頂点
までのアイテムを使って、重さ
以下になるように選んだときの価値の最大値
遷移元は親なので から遷移します。頂点番号を1-indexedで取って、初期状態は
としておくと都合が良いです。
また 以下としておくと後で便利で、そのためには初期状態を
とすれば良いです。
この時点でクエリ のうち
であるものには答えられます。DPパートの計算量は
です。
下側を全探索
クエリ のうち
であるものを処理します。このとき図の深さ
まではDPで計算できているので、
から遡って深さ
までの頂点のアイテムを集めます。これは
個以下なので、最大
通りの選び方を全探索できます。
ある1つの選び方 について、その価値合計が
、重みが
だったとします。そして頂点
から遡ってぶつかる深さ
の頂点番号が
だったとすると、この選び方で実現可能な最大価値は
であることが分かります。
のときは無視します。
これを全ての選び方について計算して最大値を取ったものが答えになります。
後半パートの計算量はクエリあたり にすることができます。各選び方について独立に
を計算していると余分に
が掛かってしまうので少し工夫しましょう。ビット全探索で実装したときに、選び方のビット列
に対応する値
を
で求めたいです。これは
のMSB(最上位ビット)を管理しておくことで、
のときの結果
から差分更新できます。これで選び方1つあたりの計算量を
にできます。
これで全体計算量 が達成できます。
ACコード
Submission #14246887 - Tokio Marine & Nichido Fire Insurance Programming Contest 2020
Codeforcesのレーティング計算の仕組み
Codeforcesのパフォーマンスって計算できるんだろうか、という話が挙がる機会が多いので、レーティング計算について調べた内容をまとめます。
情報源
公式な情報源はこれです。
Open Codeforces Rating System [updated on October 2015] - Codeforces
5年前に公開されたソースコードへのリンクもありますが、CF-Predictorのコードと少し違う点があり、時期を考えるとCF-Predictorのほうが正確そうなので、そちらを読んでいます。
この記事は2020年6月時点でのCF-Predictorのコードを元にしています。
アウトライン
レーティング計算のアウトラインは以下のようになっています。ここでの「参加者」や「順位」はratedな参加者を対象にしたものを指します。
- 各参加者に対して、以下のようにレーティング変動値を計算する。
- 本人と他の参加者のコンテスト前のレーティングから、そのコンテストにおける本人の seed (後述)を計算する。
- 本人がコンテストで取った順位とseedの相乗平均を取る。これを AverageRank と呼ぶ。
- seedの計算の逆を用いて、「レーティングいくつならseedとAverageRankが一致していたのか」を計算する。これを expR と呼ぶ。
- expRとコンテスト前のレーティングの相加平均を 新レーティング(の調整前の値) とする。これによりレーティング変動値を計算する。ただし変動値は
の範囲に収める。
- レーティングのインフレ/デフレを抑制するため、レーティング変動値の合計がおよそ
になるように調整する。
- まず全員のレーティング変動値合計が
になるように一様な値を加算する。
- その後、コンテスト参加者
人のうちトップ
人について、その中でのレーティング変動値合計が
になるように一様な値を加算する。ただしこのときに加算される値は
の範囲に収める。
- まず全員のレーティング変動値合計が
これに加えて2020年5月ごろ以降は、あくまで「表示上の」補正として参加回数が6回未満の人のレーティングには参加回数に応じたマイナス補正が掛かっています(リンク)。
seedとは
イロレーティングに基づいて計算された「順位の期待値」とでも呼ぶべき値です。
イロレーティングは1対1での対戦における勝利/敗北確率を定義しています。ある参加者(本人)がレーティング であるとき、レーティングが
である他の参加者に敗北する確率がそれぞれ計算されます。これを自分以外の参加者の
全てについて計算して和を取り、1を足したものがseedです。
seedの値は の増加に対して単調減少なので、逆算する際には二分探索が用いられています。競プロは競プロの役に立つ。
各コンテストにおける各参加者のseedはCF-Predictorで閲覧できます。
いわゆる25%説について
レーティング計算において、最近のコンテストの成績の重みが25%を占めているという話があります。これは、
- AverageRankを計算するのに、現レーティングからのseed値と実際の順位の相乗平均を
- expRを計算するのに、現レーティングとexpRの相加平均を
用いていることに由来しています。何かと何かが の割合で混合されている訳ではないので注意が必要です。
いわゆるパフォーマンスについて
AtCoderではパフォーマンスという値がレーティング計算の途中結果として生成され、ユーザーにも公開されています。「このコンテスト(と参加者集団)でこの順位を取ったらパフォーマンスはこの値」というのが自分のレーティングに依存せずに計算されるため、コンテスト1回ごとの出来栄えをレーティングの尺度で測るために重宝されています。
AtCoderではCodeforcesと異なり、本人がコンテストで取った順位から直接「レーティングいくつならseedと実際の順位が一致していたのか」に相当する値InnerPerfを求めています。これにコンテスト毎に設定されている上限を付けたものがパフォーマンスです。なので本人のレーティングの影響が混入していません。
一方でCodeforcesでは早い段階で本人のレーティングが計算に混入してしまうため、レーティング変動からパフォーマンスに対応する値を取ることは難しいと考えます。Codeforcesのレーティング計算とは関係なく、AtCoderと同様に取った順位を直接用いてseedの逆計算を行えばそれっぽい値は出ると思いますが、そのためには全参加者のレーティング情報が必要です。
実用上は、「CF-Predictorを見て自分の順位とseedの値が近い人のPrevious ratingを見る」くらいが良いのではないかと個人的には思っています。もしPrevious ratingから計算されるseedと同順位を取った場合、ゼロサム調整前のレーティング変動値が になるはずだからです。これは「あるパフォーマンスを無限回取り続けるとそのレーティングに収束する」という挙動にある程度合っています。
Educational Codeforces Round 89 F. Jog Around The Graph
問題概要
頂点
辺の重み付き無向グラフが与えられる。グラフは単純かつ連結である。
正整数 について
を「頂点
から始まってちょうど
回移動する経路の、通った辺の重み合計の最大値」と定める。この経路では同じ辺や頂点を複数回通っても良い。
与えられた正整数 に対して、
を
で求めよ。
制約
- 各辺の重み
について
- グラフは単純かつ連結
解法
最適経路についての考察
考えるべき経路は以下のようなものに限定することができます。
- 頂点
からスタートして、通る頂点・辺が重複することなく、ある頂点
に移動する。
- その後、
に接続しているある辺を往復し続ける。
これは以下のように証明できます。任意の経路について、その経路で最も重みが大きい辺に注目します。その辺に到達する前のサイクルを排除して、到達した後は元の経路と同じ合計ステップ数になるまでその辺を往復し続けるような新しい経路を考えます。これは上記の条件を満たし、重み合計が元の経路のもの以上になります。よって上記の条件を満たすものだけを考えれば十分であることが示されます。

通る頂点・辺が重複しないということは、往復パートに入るまでに通る辺の本数は 本以下です。よってまずは
の範囲で以下のDPを回します。
頂点
からスタートして辺を
回移動して頂点
にいるような経路の、重み合計の最大値
このDPの計算量は であり、これで
は求められます。あとは往復パートです。
このDPの から、各辺の重みについて「
ステップ目以降で重み
の辺を往復し続ける場合、それまでの
ステップで得られる利得の最大値は
である」という情報が得られます。
つまりやるべきことは、 を
について合計することです。これはCHT(Convex-Hull Trick)が使える形になっています。
CHTの活用
まずは先ほどの直線群をCHTに掛けて「要らない直線」を除外します。そうすると各直線が最大値を実現するような の範囲は、傾きが小さいものから順に並ぶ区間になります。
が大きいので全ての
を試すことはできません。なので最大値を実現する直線が切り替わる場所を二分探索で求めることにします。傾きが小さい順に見ていけば左端は分かるので、「今見ている直線が最大値を実現するか」を判定基準として右端を二分探索すれば良いです。
1つの直線が最大値を取るような区間において は等差数列になるので、両端が分かれば等差数列の和の公式で計算できます。
個の境界を探すのに1回あたり
かかるので、後半パートの計算量は
になります。
CHTなしでも間に合う
CHTを使う方法のメリットは、上記の二分探索において「今注目している直線が、ある に対して最大値を実現するか?」を効率的に判定できることです。ただし今回は直線の数が高々
本であり
なので、CHTを使わずに毎回全部の直線を計算しても良いです。
※ただ「各直線が最大値を実現するような の範囲は、傾きが小さいほうから順に並ぶ区間になる」という性質は変わらず使うので、CHTの考え方は必要になります。
後半パートの計算量が になりますが、これでも間に合います。
ACコード
AtCoder Grand Contest 045 C - Range Set
解法
必要十分条件への言い換え
ある01文字列が与えられた時に、それが操作によって生成可能であるかを判定することを考えます。
ここで今回のように「塗り潰す」系の操作の場合、「判定したい文字列から逆順で操作を行い、初期状態に戻せるか?」と考えると見通しが良くなることが多いです。塗り潰す操作を逆に見ると「塗り潰す前は何でも良い」と思うことができるので、「何でも良い」領域をどんどん広げていくことで初期状態にマッチさせることを目指します。
具体的には、今回の問題における逆操作は
- 操作0:
0または*が個連続している領域(混ざっていても良い)を、全て
*に置き換える。 - 操作1:
1または*が個連続している領域(混ざっていても良い)を、全て
*に置き換える。
と記述することができます。ここで * は「0 と 1 のどちらでも良い」ことを意味します。
初期状態は全て 0 なので、判定したい文字列からこれらの操作を続けて 0 または * しか存在しない文字列にできれば生成可能ということになります。ただし 0 または * しか存在しない文字列はさらに操作0を繰り返すことで必ず全て * にできるので、条件を「全て * にできること」と言い換えても良いです。こうすると最後の条件において 0 1 の区別がなくなります。
さらに考えると、これは 個以上の連続する
* を作ることができれば必ず達成可能であることが分かります。これが1箇所できてしまえば、あとはそれに隣接する1文字を * に変える操作が必ず可能で、文字を全て * に変えることができるからです。
最後の条件に 0 1 の区別がなくなったので、 として解くことができます。もし
である場合は生成可能な文字列の
0 1 を反転させると思うことでスワップすることができるからです。このときある01文字列が生成可能である必要十分条件は、
- 操作0、操作1の繰り返しによって、
*が個以上連続している領域を作ることができること。
です。操作1を1回行った時点で条件が満たされると考えると、これは
- 操作0の繰り返しによって、
1または*が個以上連続している領域を作ることができること。
と言い換えることができて、* を 1 に置き換えてしまうと結局
- 連続する
個以上の
0を全て1に置き換えた後、1が個以上連続している領域が存在していること。
とまで言い換えることができます。
数える
先ほどの必要十分条件を満たす01文字列を数えます。
もし 個以上の
0 を 1 に置き換える操作がなければ、次のようなDPで条件を満たさないものを数えることができます。
前から
文字を決めて、直前の連続している
1の個数が個であって、これまでの遷移で
となったことが一度もないような01文字列の個数
※余事象を考えていることはあまり本質ではなくて、例えば「一度でも 1 が 個以上連続したことがある」というフラグを足すことで直接数えることもできます。
実際には 0 を 1 に置き換える操作を考慮する必要があります。つまり 0 が 個以上連続している領域は、
が表現している「直前の連続している
1 の個数」に加えてあげる必要がある、ということです。
これを処理するために添字を増やします。 を以下のように定義します。
- 前から
文字を決めて、
- 直前の連続している「
1または個以上の連続した
0」の合計個数が個であって、
- 直前の文字が
であって、
- 直前が連続した
個以上の
0である()/ない(
)状態で、
- これまでの遷移で
となったことがないような01文字列の個数
からの遷移を考えましょう。まず普通に
1 または 0 を足す遷移では遷移後の状態は以下のようになります。
1を足した場合、は
増え、
は
になり、
は
になる。
0を足した場合、もし遷移前のが
であれば
が
増えて遷移する。そうでなければ、
がともに
になって遷移する。
それとは別に、 のときは「
0 が 個連続する領域が始まる」という遷移を特別に考える必要があります。これは最初または
1 の直後のみ行います(このためにフラグ があります)。この時の遷移は、
に係数
で遷移する。
- その代わり「普通に
0を回連打した遷移」を算入してはいけないので、そのときの遷移先である
にあらかじめ係数
で遷移しておくことで打ち消す。
と処理することができます。
初期条件は とすれば良いです。このDPを計算することで答えを求めることができます。
ACコード
Codeforces Round #641 (Div. 1) F1. Slime and Sequences (Easy Version)
問題概要
※解説の都合上、0-indexedで表記します。
正整数 が与えられる。長さ
の非負整数列
が以下の性質を満たす時、これを「良い数列」であると呼ぶ。
に1つ以上含まれる任意の正整数
について、
かつ
かつ
であるインデックスの組
が存在する。
のそれぞれに対して、全ての良い数列について値
が登場する個数の合計値を
で求めよ。
制約
解法
全単射の構成とその証明
公式解説の初手が天才なので天下りの書き方になってしまいますが、良い数列を以下のように長さ の順列と一対一対応させます。
- 順列
について、隣り合う要素の間に大小関係に応じて
>または<を書き込む。 を「上記手順で
よりも左側にある
<の個数」と定義する。このときは隣り合う要素の差が
または
の広義単調増加数列となる。
となるように数列
を構成する。
これが良い数列と正しく一対一対応している(全単射になっている)ことを証明します。以降の証明では、 と
のインデックスを
、
のインデックスを
と表記しています。
順列→良い数列
順列から数列は一意に構成されるので、構成されたものが良い数列であることを示します。
順列 に書き込んだ
< のうち、左から 番目(
は
始まり)にある
< を挟む2要素を考え、これらのインデックスを とします。このとき
< が書かれていることから であり、かつ
の決め方から
と
です。よって
がそのまま良い数列を満たす条件に合う
のインデックスの組になります。
全ての < の個数は に一致し、
の全てについて上記が成り立つので、
は良い数列です。
良い数列→順列
良い数列から元の順列が一意に復元できることを示します。
まずは中間の数列 を復元します。順列から生成される
は広義単調増加なので、これは即ち
をソートしたものになります。
ここで に値
が複数含まれる場合、
である
たちと、
である
たちがどう対応するかの選択肢があります。しかし不等号の条件に矛盾しないようにするとこの対応は一意に定まります。具体的には
として同じ値が並んでいるゾーンで
< が出現してはいけないので、 はこのゾーン内で降順になっている必要があります。
そして降順になるように割り当てた場合、左から 番目の
< を挟む箇所に存在している の要素を
とすると、これは「
である
の最小値」と「
である
の最大値」であり、
が良い数列であることから必ず
となります。
よって良い数列に対応する元の順列はちょうど つ存在することが示されました。
数え上げ
証明だけでかなりの行数を使ってしまいましたが、求めたいのは「全ての良い数列についての、値 が登場する個数の合計値」でした。良い数列
の代わりに、
通りの順列
全てから生成される
に対して数えることにします。
と
の組み合わせ
それぞれについて、
となるような順列
の個数が求められれば良いです。これはつまり、
以降の値の並びは
に関与しないので、まずは関与しない
個の要素を選んで並べる方法の数を求める。これは
通り。
- 残った
個の要素の並べ方であって、その中に
<をちょうど個含むような方法の数を掛ける。
と求めることができます。
2.の値については、小さい値から処理していく挿入DPを用いて前計算することができます。具体的には、
値
を含む長さ
の順列であって、
< をちょうど 個含むものの個数
と定義します。
からの遷移として、ここに値
を挿入することを考えます。このとき
- 先頭または既に
<である隙間に挿入する:挿入箇所は通りで、
<の個数は増えない。 - 末尾またはいま
>である隙間に挿入する:挿入箇所は通りで、
<が1個増える。
となるので、それぞれ係数を掛けて または
に遷移します。
これを前計算しておけば、先ほどの2.の値としてそのまま使えます。これで全体計算量 で答えを求めることができて、Easy Versionが通ります。