Codeforces Round #595 (Div. 3) D2. Too Many Segments (hard version)
お題箱より。
問題概要
整数を端点とする 個の閉区間
が与えられる。これらから0個以上の区間を捨てて、全ての整数点について「その整数点を含んでいる区間は
個以下である」という状態にしたい。
捨てる区間の最小個数と、その選び方の1例を求めよ。
制約
解法
小さい方を左として、左から順番に整数点を見ていきます。このとき各整数点について「今見ている整数点を含んでいる区間が 個以下となる」ように区間を捨てていきます。
具体的には「残す区間であって、今見ている整数点を含むもの」の集合を管理するようにします。そして整数点 を見る時には以下の処理をします。
を左端とする区間を、いったん全て集合に入れる。
- 集合に含まれる区間数が
個を超えている場合、
個以下になるまで↓を繰り返す。
- 集合の中で右端が最も右にある区間を捨て、集合から取り除く。
- 集合の中に
を右端とする区間がある場合、この区間から出るので集合から取り除く。
この方法で捨てる区間の個数が最小となり、その選び方の1例を求められます。
その理由を考えてみましょう。この処理を左側の整数点から順に行っていくと、整数点 を見るときにはそれより左の整数点は既に条件を満たしています。つまり集合に入っている区間が
より左側のどこまで伸びているかは、もはや考えなくて良いです。2.において捨てる区間を選ぶときには、
より右側で最も邪魔になりやすい区間、つまり右端が最も右にある区間を捨てるのが常に最適になります。
つまり区間を管理する集合においても、左端は必要なくて右端の値(と出力のためのインデックス)が保持されていれば良いです。この集合に必要な機能は
ことです。これはC++であれば set 等で実現できます。
言語機能にない場合は、BIT等に入れておいて二分探索する等の方法があります。もしくはPython等にもある優先度付きキューで1.と2.の機能は実現できるので、3.を工夫して代用しても良いです。集合に入っている値の頻度表を別途作っておき、「区間から出る」ことで除かれるはずの要素数を別途計算しておけば、その分だけキューの中の要素数から差し引くことで同じことができます。
ACコード
- (C++ set利用)Submission #63665793 - Codeforces
- (Python heapq利用)Submission #63666907 - Codeforces
リクエストくれた人の使用言語が分からなかったのですが、順序付き集合が使えるかどうかで若干実装が異なるのでC++とPythonの実装例を紹介しておきます。
私はこのコンテストの本番では区間加算ができるセグメント木を使いました。解法、実装手段は色々あると思います。
Kyoto University Programming Contest 2019 E - 根付き森二人用ゲーム
お題箱より。
解法
それぞれの木を小規模なゲームとして解く
スタート地点からある木に移動し、その木の葉に到達してスタート地点に戻るまでの一連の動作を考えます。このときゲームに本質的に影響するのは「次にスタート地点で手番を持つプレイヤーが交代するかどうか」だけです。これは到達した葉の深さの偶奇に依存します。
この観点で、それぞれの木に対して小規模なゲームを考えます。以下の2つのゲームを考え、それぞれの勝敗を調べます。ここで「先手」はスタート地点からその木に移動するプレイヤー(木を選ぶ人)、「後手」はその後に根から最初の移動をするプレイヤーを指します。
- ゲーム1:先手は手番を交代したい、後手は手番を交代したくないと思って行動する。結果として手番が交代すれば先手の勝ちである。両者が最適に行動するとどちらが勝つか?
- ゲーム2:先手は手番を交代したくない、後手は手番を交代したいと思って行動する。結果として手番が交代すれば後手の勝ちである。両者が最適に行動するとどちらが勝つか?
これは後退解析によって求めることができます。まず葉については深さの偶奇から手番交代する/しないが分かるので、その葉がどちらの勝ち状態であるかが分かります。あとは根まで順に辿っていき、各頂点がどちらの勝ち状態かを判定します。その判定方法は「その頂点からの遷移先に自分の勝ち状態であるものが1つでもあれば勝ち、そうでなければ負け」です。
この2つのゲームの結果から、それぞれの木は以下のように分類できます。
- タイプA:どちらも先手プレイヤーが勝つ。つまり先手プレイヤーが手番交代の有無を選べる。
- タイプB:どちらも後手プレイヤーが勝つ。つまり後手プレイヤーが手番交代の有無を選べる。
- タイプC:どちらの場合でも、結果として手番が交代する。
- タイプD:どちらの場合でも、結果として手番が交代しない。
全体の勝敗判定をする
このように分類したもののうちタイプDは勝敗に影響しません。残りの3タイプの木の個数を用いて、ゲームの状態を3つの整数の組 で表現します。入力として与えられる木を分類して求めたそれぞれの個数を
とすると、これがゲーム開始時の状態です。
単純に考えると、ここでも後退解析を使いたくなります。つまり の状態で手番を持ったプレイヤーは負けであり、DPのように値が小さい方から順番に
なる全ての
について後退解析で勝敗を求めていけば、一応判定することはできます。ただ計算時間が間に合いません。
もっと楽に判定できないか考えましょう。例えば という状態からタイプAの木を1つ消費した状態
の勝ち負けは、どちらかは計算できていませんがどちらかに定まっているはずです。ならば先手はこれが負け状態であれば手番を交代して相手に押し付け、勝ち状態であれば再び自分の手番にすることで必ず勝つことができます。
同様にタイプBの木を選んでしまうと、相手に勝てる方を選ばれてしまい必ず負けます。つまり、タイプAやタイプBの木によって選択権利を持ったプレイヤーはその時点で勝ちが確定します。
つまりこのゲームの勝敗は、以下のように判定することができます。
- タイプAの木が存在する(
である)場合、真っ先にその木を選べば良いので必ず先攻のAliceが勝つ。
- そうでない場合、手番プレイヤーはタイプBの木を選びたくないので、タイプCの木が尽きるまで選ばれ続ける。タイプCの木が尽きた時点で手番を持ったプレイヤーが、タイプBの木を選ぶ(または全ての木が尽きる)ので負ける。つまり
の偶奇により勝敗が決まる。
ACコード
Submission #7957578 - Kyoto University Programming Contest 2019
Codeforces Round #594 (Div. 1) B. The World Is Just a Programming Task (Hard Version)
問題概要
長さ の括弧列
が与えられる。長さ
の括弧列のスコアを、「
を
回だけ右巡回シフトした文字列が正しい括弧列になっている」という条件を満たす
の個数とする。
に対して1度だけ、2箇所を選んでスワップする操作を行うことが出来る(同じ位置を選んでもよい)。操作後の
の最大スコアと、そのスコアを実現するスワップ位置の1例を求めよ。
制約
解法
巡回シフトが正しい括弧列になる条件
正しい括弧列の問題では ( を 、
) を とした累積和を考えるのが定石です。この値が全て非負でありかつ最後に0になることが、文字列が正しい括弧列である必要十分条件です。
与えられた文字列について、以下のように に変換した数列
とその累積和の列
を求めます。

まず であることは大前提です。そうでない場合、シフトやスワップをどうやってもスコアは絶対に0なので適当なスワップ位置を答えて終了します。
巡回シフト後の文字列が正しい括弧列になっている必要十分条件は、 の中で最も値が小さい位置が左端になるようにシフトすることです。つまり
が最小値を取るような
の個数がそのままスコアになります。
このとき と
は同じシフトに対応するのでダブって数えてはいけません。以降は
を数える対象として扱います。
スワップが累積和に与える影響
次にスワップの影響を考えます。同じ文字同士をスワップした場合は当然何の変化もありません。異なる文字をスワップした場合には、
という変化があります。
スワップ後の累積和を と表記します。
の最小値を
とすると、
の最小値は
以上
以下の範囲に存在することが分かります。
最小値とスワップの正負を決め打ってDP
最小値の候補は5個で、スワップによって されるか
されるかは2通りです。これらを決め打って全部試します。
スワップ後の最小値として決めた値を とします。このとき、
より小さい
があってはならず、
に等しい
の個数がスコアになります。
また、左側にある と右側にある
をスワップすると仮定します。このときこの2要素の間にある累積和については
となります。
このとき は、左から順に
- ゾーン0:
である。
- ゾーン1:
である。
- ゾーン2:
である。
という3つのゾーンに分かれます。

このゾーンに基づいてDPを定義します。つまり
累積和
まで見て、
はゾーン
に属していて、
より小さい
はこれまで存在していないときの、
に等しいこれまでの
の個数(スコア)の最大値
というDPを考えることができます。
からの遷移を考えます。まず同じゾーンへの遷移があります。それに加えて今は左側にある
と右側にある
をスワップすると仮定しているので、
であるときにはゾーン0→1の遷移、
であるときにはゾーン1→2の遷移が起こり得ます。
遷移後のゾーンを とします。遷移後の累積和
の値は、元の
に遷移後の所属ゾーン
に応じた変化量を足したものです。これが
より小さい場合は遷移を却下します。ちょうど
である場合はスコアを1増やして、そうでない場合にはスコアそのままで、
に遷移します。
最後まで遷移すると、 には「スワップしなかった場合の最大スコア」、
には「スワップした場合の最大スコア」が入っています。前者を採用する場合は適当に同じ位置をスワップしたことにします。後者を採用する場合はDPの復元を行ってスワップ位置を特定します。
これを最小値の候補5個とスワップによって変化する値2通りの組み合わせ全てについて試し、最も大きいものが答えです。
ACコード
本番の実装が分かりにくかったので書き直しましたが、定数倍が悪くなってちょっと実行制限時間ギリギリになりました…なので両方リンク貼っておきます。この記事の記法等に合わせているのは書き直しコードのほうです。
AtCoder Beginner Contest 143 F - Distinct Numbers
解法
色々な解法があるみたいですが…この記事ではそれぞれの について独立に解きます。ある
について解くときには、可能な操作回数には単調性があるので二分探索できます。
ある と操作回数
を固定したときに、操作を
回行えるかどうか判定する方法を考えます。まず
は必ず満たす必要があります。その上で
の中から使う整数を
個選んで
(*) 全部で 個の整数から、「異なる
個の整数を取り除く」という操作を
回行うことができる
かどうかを判定したいです。このとき(*)の必要十分条件として、
全ての整数値 について、
個の中に
が含まれる個数は
個以下である
というものがあります。
必要性については、もし 個を超える整数値が存在する場合はそれらを
回の操作で全て取り除くことができないことから示せます。
十分性については、以下のようにすると実際に構成できることから示せます。(Special Thanks:てんぷらさん)
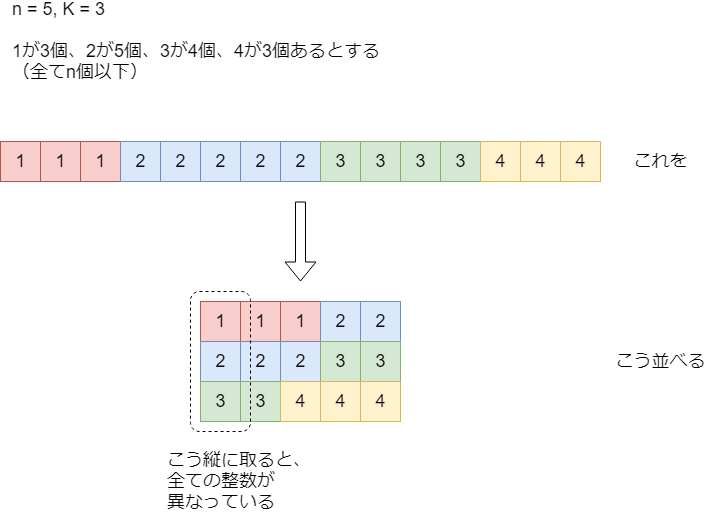
つまり から各整数値を
個以下取ってきて、合計で
個確保できればOKということになります。これは以下のように解くことが出来ます。
まず を「整数値○が
個、整数値△が
個…」という風に集計したときの数列
を求めて、これをソートしておきます。このとき各整数値を
個以下取ろうとすると、
であるような
については全て取る。
であるような
についてはそれぞれ
個ずつ取る。
ということになります。1.と2.の境界を二分探索などで求めて、1.については累積和を求めておくと、取れる個数の合計を効率的に求めることが出来ます。これが 以上かどうか判定すれば良いです。
この解法だと全ての を試すので
、答えを求めるための二分探索で
、
を満たす境界を求めるのに
で、全体
になります。ちょっと重いですね。
を満たす境界を全ての
について前計算しておくと
が1個落ちるなど、計算量の改善は色々あると思います。
ACコード
AtCoder Regular Contest 077 E - guruguru
お題箱より。
後半は公式解説と少し違う方法になっています。
解法
お気に入りで節約できる回数を定式化する
ある1つの に対する
から
への移動を考えます。まず簡単のため、
と仮定しておきます。移動元と移動先をそれぞれ
と書くことにします。
お気に入りボタンを使わずに から
に移動するボタン回数は
です。ここで「
と比べて、お気に入りボタンがもし値
に設定されていたら回数をどれだけ節約できるか?」という値をそれぞれの
について考えましょう。この値を
と書くことにします。
これは以下のように、 の範囲において
という等差数列になり、他は0になります。

ただし のときは途中で明るさがループします。これを扱うのは面倒なので、「ループするときは2周回す」テクニックを使います。
のときは移動先
は2周目にあると考えて、
とします。そして
も2周分、つまり
の範囲で値を持つことにします。このときお気に入りが
に設定されている時の節約回数は、1周目と2周目を合わせて
と求めればよいです。
これを 回の移動について全て足したもの、つまり
が「お気に入りを
に設定したときに、お気に入りを全く使わない時に比べて節約できる合計回数」です。この最大値を、お気に入りを全く使わない時の合計回数
から引いたものが答えになります。
こうなると残る課題はそれぞれの を求めること。つまり「数列に『ある区間だけに等差数列を足す』という操作をいくつも行った結果」を効率的に求めることになりました。
等差数列の重ね合わせを求める
ここで使うのは「階差数列」を利用するテクニックです。
話が変わりますが、「いもす法」というテクニックがあります。1次元のいもす法は「ある区間だけに同じ値を足す」という操作をいくつも行った結果を効率的に求めるテクニックです。これは以下のように、階差数列を利用しているテクニックと思うことが出来ます。

「ある区間だけに同じ値があり、区間外は全て0」という数列は、1階の階差数列を取ると上記のように0でない値が2箇所だけになります。
「階差数列を取る」という操作と「累積和を取る」という操作はちょうど逆の操作になっていて、かつこれらの操作には線型性があるので、足したい数列たちの階差数列を足してから累積和を取ることで元の数列たちの和が得られます。
同様のことが等差数列でもできます。今回の のように「ある区間だけに等差数列があり、区間外は全て0」という数列は、2階の階差数列を取ることで0でない値が3箇所だけになります。

よって 回の全ての移動についてこれらの値を足した後、2回累積和を取ることで全ての
に対する
を求めることができます。
ACコード
Codeforces Global Round 5 E. Balanced Binary Search Trees
問題概要
以下の条件を満たす根付き木を二分探索木と呼ぶ。
- 任意の頂点
について以下が成り立つ。
- 「左側の子」と「右側の子」がそれぞれ高々1個存在する。
- 左側の子孫が存在する場合、それら全ての頂点番号は
より小さい。
- 右側の子孫が存在する場合、それら全ての頂点番号は
より大きい。
頂点番号 の
頂点からなり、以下の条件を満たす二分探索木の個数を
で求めよ。
- 頂点数
の二分探索木の中で、各頂点の深さの合計が最小である。
- 任意の頂点
について以下が成り立つ。
- 左側の子が存在する場合、その頂点番号の偶奇は
と異なる。
- 右側の子が存在する場合、その頂点番号の偶奇は
と等しい。
- 左側の子が存在する場合、その頂点番号の偶奇は
制約
解法
というハッタリがありますが、実は条件を満たす木は高々1つです。その理由を説明します。
まず深さの合計が最小であるという条件は、直感的にはできるだけ根に近いところに頂点が集まっているということです。これは具体的には、木の最下段以外は頂点が詰まっている、つまり完全二分木になっているということを意味します。
ということでまずは、完全二分木になっている部分の深さの最大値 を求めます(根を深さ0とします)。これは
を満たす最大の
として求められます。このとき深さ
以上の頂点は存在しません。

条件を満たす木の構成を、以下のように試みましょう。
- まず頂点番号
のうち
個を使って、偶奇の条件を満たすような深さ
までの完全二分木を作る。
- 上記で使わなかった(飛ばした)頂点たちを、深さ
の段に適切に付けられるか考える。
ここで飛ばした頂点は、大小関係から「付ける場合は、深さ のこの頂点のこちら側に付けなければいけない」という位置が一意に定まります。つまりもし連続して2つ以上の頂点が飛ばされている場合、それはどう頑張っても深さ
の段には収まりません。これが完全二分木を作る上で強い制約になります。
完全二分木の頂点番号を、番号の小さい位置から順番に決めていきます。番号が最も小さい頂点は左下の頂点ですが、連続して1, 2を飛ばしてはいけないので、左下の頂点は1または2である必要があります。これはとりあえず両方試すことにします。
ある1つの頂点の偶奇が決まると全ての頂点の偶奇が決まります。各頂点の偶奇が指定され、2つ以上の頂点番号を飛ばしてはいけないので、全ての頂点番号が小さい方から順に一意に定まっていきます。
あとは飛ばした頂点が深さ の段に適切に付くかどうかを確認します。頂点番号を飛ばすようなパターンを実際に列挙してみると、ほとんどの飛ばした頂点は偶奇条件に合うように
の段に上手く収まります。NGとなるのは完全二分木の右下の頂点番号が
ではない場合です。
を超えている場合は当然NG、
以下である場合はそれ以降を連続で飛ばすことになるのでNG、
である場合はその右下に偶奇の異なる
を付けると条件違反になるのでNGです。
このことから結局、完全二分木の右下の頂点番号は必ず にならないといけないので、左下の頂点の偶奇も片方しか条件を満たさないことになります。これが、条件を満たす木が高々1つである理由です。
以上の考察より、私の解法は以下のようになりました。
- 完全二分木の深さ
を、
を満たす最大の
として求める。
- 完全二分木の左下の頂点の番号を1または2と仮定してそれぞれ試す。DFSのように完全二分木の頂点番号を小さい順に決めていく。その結果、右下の頂点番号が
となった場合、これは条件を満たす。
- 条件を満たす木の個数を出力する。これは高々1個である。
もしくは、答えが1になる を並べてみると単純な漸化式を持つ数列になるようです。これを実験等で突き止めて信じる心を持てば、実際に木を構成しなくても解くことができます。
E、10万以下で作れるN pic.twitter.com/qkWyfLih8z
— アルメリア (@armeria_betrue) October 16, 2019
ACコード
Codeforces Round #590 (Div. 3) E. Special Permutations
お題箱より。
Editorialのソースコードがよく分からないというリクエストだったんですが、見たところ確かによく分からなかったので、私の解法を書きます。
問題概要
長さ の順列
を
と定義する。
長さ の整数列
(
)が与えられる。長さ
の順列
に対して、
の値を「
において隣り合う2要素の組全てについて、その2整数の
での距離を求めたものの合計」と定義する。
それぞれの に対する
の値を求めよ。
制約
解法
における隣り合う2要素の組それぞれについて、それが
の値にどう影響するか考えていきます。
隣り合う2要素が同じ整数である場合は、距離はゼロなのでその組は の値に影響しません。異なる値である場合、これらを小さい方から順に
と表記することにします。
整数 の距離は、
それぞれにおいていくつになるでしょうか。これは以下のように少ないパターン数に分けられることが分かります。
のとき、
において
の並びはそのまま保持されるので、距離は
。
のとき、
において
と
の間にある整数
が先頭に移動するので、距離は
。
のとき、
において
が先頭で
が
番目にあるので、距離は
。
のとき、
において
が先頭で
が
番目にあるので、距離は
。
のとき、
において
の並びはそのまま保持されるので、距離は
。
ざっと書きましたが、パターンはこれだけです。これらの値がそれぞれの に加算されます。同じ値を取る連続した区間(または1点)を1回の範囲加算で扱えると見なすと、これは高々5回の範囲加算で処理することができます。
における隣り合う2要素の組は
個あるので、結局は高々
回の範囲加算を行った結果が答えになります。そしてたくさんの範囲加算を行った結果を得るための方法と言えば「いもす法」です。これで解くことができます。