2018-12-02

HACK TO THE FUTURE 2019 本選オープン　参加記録

AtCoder プログラミング競技プログラミングマラソンコンテスト

HACK TO THE FUTURE 2019 本選オープン - AtCoder

オープンコンテスト3位！

f:id:betrue12:20181202000519p:plain

解説というほどのものは書けないので、「こんな感じのことをしました」というのをつらつら書いていく感じになります。

最初に考えたこと

中盤まではスキルに投資することが重要だが、終盤は無駄なのでひたすら仕事をしたい。
スキルは高レベルほど上げにくくなるので、特化するより均等に上げたほうが費用対効果は高そう。
依頼は期間終了ターンもしくはその少し前で受けることを考えたい。依頼がいっぱいあるので、極論「そのターンに終了する依頼」だけを見てもよさそう。
面倒なことは考えたくないので、依頼の要求スキルレベルや期間の傾向を解析したりするのはとりあえずやらない。

ということで、こんな感じのものを書きました。

事前準備
- 依頼を終了ターンで分類しておく。
- 目標スキルレベルを決める。
～900ターン目
- 一番低いスキルレベルで一番若い番号のものをスキルアップ候補とする。そのスキルのレベルが目標レベル未満で、かつトレーニングをするお金があるならトレーニングをする。
- トレーニングをしない場合、そのターン～10ターン後までに終わる依頼の報酬を全部計算し、一番高いものを受ける。（これはバグって機能していなかった）
901ターン目～
- そのターン～10ターン後までに終わる依頼の報酬を全部計算し、一番高いものを受ける。（これはバグって以下略）

この提出がこれ（2.96億点）。10ターン後と10ターン前を間違えて、結局そのターンに終わる依頼しか受けられないようになってました。ひどいですね。

これを書いて試してみたところ、

目標スキルレベルは高ければ高いだけ結果がよくなる
スキルレベルが全て10になるのがだいたい600ターンくらいで、かなり余裕がある

ことが分かりました。そのため以降はスキルレベルを10まで上げきることを前提に考えました。

スキル上げフェーズとひたすら稼ぎフェーズ

ということで、フェーズを2つに分けてみます。

スキルレベルがオール10になるまで
- なるべく早くスキルレベルをオール10にすることを考える。
- スキルを上げられる場合、必ず上げる。対象スキルの選択は前と同様。
- スキルを上げられない場合、そのターン～ $k$ ターン後に終了する依頼から最も良いものを受ける。
スキルレベルがオール10になった後
- もうお金を稼ぐだけなので、後ろから順番に受ける依頼を決めていく。

$k$ は適当に試して決めます。 $k$ が大きいと候補が広がる反面、美味しい依頼を早く取ってしまい損をする可能性があります。このときは $k=20$ くらいになりましたが、後々の改善をした後だと $k =0$ が一番良くなりました。

スキルレベルがMAXになった後は、後ろから「最も報酬の高い依頼」を選んでいきます。本番中はこれが厳密に最適だと信じて疑いませんでしたが違いますね…ただ、美味しい依頼を最終日に選択できる可能性はとても高くなり、なかなか良い結果になったとは思います。

このアルゴリズムを書いてそこそこパラメータ調整したのがこれ。3.19億点まで伸びました。

所用のためここで少し離脱。

美味しい依頼はスキルよりも優先

用事を終わらせてPCの前に戻れたので、頭の中で考えていたことを試していきました。

まずスキル上げフェーズにおいて、トレーニングできるお金があるときはトレーニングをしていましたが、美味しい依頼があるときはそっちを受けてもよいのでは？という案。

「美味しい依頼」の基準は、最終的には「いままでの依頼の最大報酬× $k$ 以上の依頼であれば優先」という感じになりました。 $k$ は1.3くらい。

実装はこれ、結構伸びがよくて3.40億点。この提出ではいままでの最大報酬ではなく1つ前の依頼の報酬を使っています。

スキル上げ順番の操作

次に、今まで避けていた依頼の傾向解析。あまり複雑なことはしたくなかったので楽そうなものを選びました。それはスキル上げ順番の操作です。

スキルを上げる時、均等に上げていくのは変えません。ですが例えばスキルレベルが 2, 2, 2, 2, 2, 2, 2, 2, 2, 2 という状態から、どのスキルを真っ先に上げるべきでしょうか？

すごく感覚的に言うと、「スキルレベルがだいたい2～3くらいになっているであろうターン」において、「要求最大スキルレベルが3である、高報酬の依頼」があるとき、そのレベル3が要求されているスキルを優先的に上げるのがよさそうです。

これを実装に落とすと、

各スキルレベルごとに、「だいたいスキルレベルが $(k-1)$ ～ $k$ であるようなターンの範囲」を、サンプル1の実行経過などを見て決める。
依頼ごとに、もし「要求最大スキルレベル」と「依頼終了ターンが上記範囲内にあるようなスキルレベル」が一致していれば、そのレベルにおいてそのスキルを早く上げることは重要とみなし、その依頼の基本報酬額を評価に加算する。
トレーニングの時には、各スキルレベルごとに評価が高いスキルから優先的にトレーニングをしていく。

という風になります。これもかなり伸びがよくて3.56億まで上がりました。これが実質的には最後の有意な改善でした。

その後、上記「ターンの範囲」をテストケースごとに決めるような処理を入れてみましたが、結果は微増。残り時間がなかったので場当たり的にコードを書き直して実装がぐちゃぐちゃになりました。このスコアでコンテストを終えました。

振り返り

~~重い実装をするとバグるので~~予選の反省としてあまり凝ったことをせずシンプルに考えるのがよいということを学んだので、難しそうなものはどんどん後回しにしてシンプルな解法を心がけました。

スキルレベルを最大まで上げてよい、2フェーズ化、後半は後ろから貪欲という主要な知見を早めに確立できたのはとても良かったと思います。

そこからの改善はわりと場当たり的で、結構運良く思いつきが当たっていったなという印象です。

反省点としては、実行時間がダダ余りになって有効に使えなかったこと。予選のように試行回数で稼ぐことは頭をよぎりましたが、何をパラメータとして回せばよいかのイメージが持てなくて実装に落とせませんでした。

あと後ろから貪欲が最適とは限らないことに気づけなかったのはアルゴやってきた競プロerとして普通にダメですね。実際ここで大量の報酬を稼いでいるので、改善効果は高そうです。

さいごに

まさにゲームのAI（機械学習とかそんなんじゃなくて、いわゆるコンピュータ側の行動プログラム）を組んでいるみたいでとても面白い問題でした。シミュレーションゲームの敵側の行動なんかは、こんなことを考えながら組んでるのかなと少し思ったり。

成績としてはかなり良かったですが、「なぜ良かったのか」がいまいち分からず…運が良かったんですかね。マラソンに慣れてくるとこのあたりの感覚が鍛えられて、効果的に復習できるようになるのでしょうか。もう少し場数を踏む必要がありそうです。

2018-12-01

Rubyで競プロするときのTips

Ruby 競技プログラミングプログラミング

ある程度知見が溜まってきたのでまとめていきます。

各オンラインジャッジのRuby環境

2018年12月くらいの情報です。

サイト	バージョン
AtCoder	2.3.3
Codeforces	2.0.0
yukicoder	2.5.3
AOJ	2.4.0

この記事は基本的にAtCoderの2.3系を対象に書いていきます。

Codeforcesはちょっとバージョンが古いのと、実行時間制限がキツ目なので私はRubyを使っていません。

入出力編

基本的な入力。

N = gets.to_i               # 単一整数
a = gets.split.map(&:to_i)  # スペースで区切られた複数の整数
a = N.times.map{gets.to_i}  # 縦に並んだ複数の整数。たまにある
S = gets.chomp              # 文字列。chompを付けないと改行文字がついてくる

以下のような形式の入力もよく見ますね。

N
a_1 b_1
...
a_N b_N

これは次のように書くとスマートです。

N = gets.to_i
a, b = N.times.map{gets.split.map(&:to_i)}.transpose

# [[a_1, b_1], ..., [a_N, b_N]] を転置して
# [[a_1, ..., a_N], [b_1, ..., b_N]] にする

出力は puts を使うとよいです。数値も文字列も出力できて、改行文字が自動で付与されます。

数値編

多倍長整数

Rubyの整数は自動的に桁数が拡張されるため、算術オーバーフローはありません。

10**100    #=> 10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

とはいえ、あまりに桁数の多い多倍長整数を計算し続けているとTLEやMLEになります。

負の数を含む剰余計算

bが正のとき、a % bは必ず0以上となります。

-1 % 3    #=> 2

言語によっては上記の結果は-1となるかもしれません。競技プログラミングではどちらが扱いやすいでしょうか？個人的にはRubyの挙動のほうが好きです。

ちなみにほとんどやらないと思いますが、-1 % -3は-1になります。

浮動小数の出力

浮動小数をputsなどで出力する場合、値が大きくなると指数表記になります。

puts (10**15).to_f    # 出力: 1.0e+15

内部的にはto_sが実行されているのですが、リファレンス上は「人間が読みやすい形の文字列表現」という何ともスッキリしない書かれ方がされています。

実際にこの問題の出力例3に示されている数は、putsを用いると1.0e+15と出てしまいます。（ただ、この問題はそれでもジャッジが通りました。）

解決方法はsprintfなどを使うことです。

puts sprintf("%f", (10**15).to_f)    # 出力: 1000000000000000.000000

1e9のようなリテラル表記

例えば C++で $10^{9} + 7$ を代入したい時にこんな書き方をします。

const int64_t MOD = 1e9 + 7;

1e9 のようなリテラル表記はRubyでもC++でも浮動小数ですが、C++では変数を整数型で宣言していれば代入時にキャストされます。

一方、Rubyの場合は変数に型がないので浮動小数のままです。整数値を代入したい場合は**を使いましょう。

MOD = 1e9 + 7    #=> 1000000007.0
MOD = 10**9 + 7  #=> 1000000007

ビット演算

ORやANDなどの基本的な演算は他言語と同様にありますが、個人的によく使うのが「整数の $k$ ビット目を取り出す」操作です。Rubyでは以下のように書くことができます。

5[2] #=> 1    最下ビットを0として、下から2番目のビット

ビットシフトなどを使って書くよりも簡潔ですね。見た目はキモいですが便利です。取り出すだけで、ビットへの代入（値の変更）はできません。

また、整数のビット長は bit_length を使って取り出すことができます。これは2.0系にはないのでCodeforcesで使うとREで死にます。

5.bit_length #=> 3

最小公倍数、最大公約数

標準で使えます。

10.gcd(4)  #=> 2
10.lcm(4)  #=> 20

素数関連

prime モジュールを使えば素数列挙や素因数分解ができます。

require 'prime'
Prime.each(15).to_a       #=> [2, 3, 5, 7, 11, 13]  15以下の素数
Prime.prime_division(24)  #=> [[2, 3], [3, 1]]      2**3 * 3**1

配列編

要素の追加/削除にはなるべく破壊的操作を使う

Rubyの配列は、先頭・末尾に対する要素の削除と追加を効率的に行うことができます。この点ではC++のdequeと似ています。

これらの操作は破壊的操作（push/pop/shift/unshift）として提供されています。もし不都合がなければできるだけ破壊的操作を使うようにしましょう。速度が全然違います。

a = a + [1]    # 非破壊的操作
a.push(1)      # 破壊的操作

配列の`max/min`より`if`や三項演算子を使う

複数の値の最大値や最小値を求めるとき、わざわざ配列を作ってmin/maxで判定するよりは、ifや三項演算子を使ったほうが速くなります。競技プログラミングでは以下のような操作をよく行いますね。

ans = #<暫定最適解>
while #<何かの条件>
  result = #<何かの計算結果>
  ans = [ans, result].max      # これは遅い
  ans = result if ans < result # こっちのほうが速い
end
puts ans

ループの深いところでminやmaxを使うとかなり遅くなるので注意です。たまに300点問題とかでもこれが原因でTLEを食らったりします。

なお、この現象はRuby 2.4以降においては改善されています。

負のインデックス

Rubyの配列で負のインデックスを取ると、「末尾から数えて $k$ 番目」の意味になります。C++のvector::backと同様、末尾の値が欲しいときによく使います。

a = [1, 2, 3]
a[-1]  #=> 3

他にも少しトリッキーな使い方があって、添字がマイナスになるところの処理を少し簡略化できます。例えば

累積和を0-indexで取ると範囲和が S[r] - S[l-1] のようになり、l=0 の時に負数になってしまう
グリッドで隣のマスにアクセスする時に、インデックスが減る方向を参照すると S[i-1][j] のようになり、i=0 の時に負数になってしまう

など。負数インデックスが例外や未定義動作になる言語では気を使わないといけないですが、Rubyでは末尾の参照になるので、末尾に「番兵」的な値を入れておくことで少しだけ実装をスマートにできます。ただ、ちょっと気持ち悪いとかバグらせそうとかあると思うので、お好みで。

配列の要素の合計

2.4だとsumが使えるのですが、2.3系以前であればinjectを使いましょう。

a = [1, 2, 3, 4]
a.inject(:+)  #=> 10
a.inject(:*)  #=> 24    たまに積も使う

二分探索

競技プログラミングでよくつかう二分探索。C++だとlower_boundやupper_boundがよく使われますが、Rubyにはもう少しだけ高機能なbsearchメソッドがあります。これは判定条件をブロックとして与えることができます。

※C++だとpartition_pointという関数で類似のことができるようですが、あまり使われていないような気がしますね…。

これはArrayまたはRangeに対して使えます。リファレンスをみる限りちょっと仕様が難しいのですが、二分探索可能な（単調な）場合において「ブロック内の条件を満たす一番左の要素」を返します。どの要素もブロック内の条件を満たさない場合はnilが返るので注意です。

(1..(10**9)).bsearch{|n| n*n >= 500}  #=>23    これはceil(sqrt(500))に相当

ブロックの中に判定ロジックが書けるので、判定ロジックが短く書けるような問題においては特に使いやすいです。こんな書き方もできます。

浮動小数の範囲オブジェクトに対しても使えますが、精度や反復回数を指定できないので競技プログラミングにおいて使うのは少し不安です。

スコープ編

定数

大文字で始まる識別子は定数となり、オブジェクトを再代入すると警告が出力されます。警告なのでまあ処理はされるのですが、気になる場合は再代入しそうなものを大文字で書き始めるのは避けましょう。競プロでは入力として与えられる整数などは定数でよいと思います。

また定数の地味なメリットですが、トップレベルで宣言した定数はトップレベルで宣言したメソッドの中で使うことができます。Rubyのグローバル変数は少し記法が面倒なので、競プロであれば入力値などのプログラム全体で使う値くらいはこのように楽に参照してもよいでしょう。

def subroutine
    a = N/2    # ここでNを参照できる
   ....
end

N = gets.to_i
....

おわり

何か思いついたら追記します。

2018-11-20

Codeforces Round #522 C. Vasya and Maximum Matching

Codeforces プログラミング競技プログラミング

Problem - C - Codeforces

考察が重かったけど、面白い問題。

問題概要

$n$ 頂点の木が与えられる。この木の辺それぞれについて辺を取り除くかどうかを考えると、その場合の数は全部で $2^{n-1}$ 通りある。そのうち「辺を取り除いた後のグラフにおいて、最大マッチングが一意に定まる」という条件を満たす場合の数を数え、 $998244353$ で割った余りを出力せよ。

制約

$1 \le n \le 3\times 10^{5}$
与えられるグラフは木

解法

木の最大マッチングが一意に定まる条件

辺を取り除いたあとのグラフはいくつかの部分木になる。そのため、まずは木の最大マッチングが一意に定まる条件を考える。部分木全てがその条件を満たしているとき、その辺の取り除き方は問題の条件を満たす。

頂点の数が1つであるとき。最大マッチングは当然0個なので条件を満たす。
頂点の数が3以上の奇数であるとき。どれだけマッチングを作っても必ず1つ以上頂点が余ってしまい、余った頂点と隣接する頂点でペアを作り変えることができてしまう。そのため条件を満たさない。
頂点の数が2以上の偶数であるとき。もし完全マッチングが存在するならばこれは一意に定まる。完全マッチングが存在しないならば、余っている頂点があるので前項と同じ理由で条件を満たさない。

ということで、頂点数が偶数のときに完全マッチングが存在するかどうかを考える。例えば、以下のようなグラフは完全マッチングを作れない。

f:id:betrue12:20181119234315p:plain

より一般的に言うと、適当に根を決めて葉からDPをしたときに、途中で「2つ以上の子について、その子以下の部分木の頂点数が奇数である」という頂点が1つでも見つかってしまうとアウトである。

これで木の最大マッチングが一意に定まる条件を洗い出せたので、本題を考えていく。

木DPをする

本題の数え上げでも、適当に根を決めて葉からDPをしていく。

以降、辺を取り除くことによって部分木を確定させることを「完成させる」と呼び、完成された部分木全てについて完全マッチングが一意に定まることを「正当である」と呼ぶことにする。

正当性を保つためにやってはいけないことは2つあり、

頂点数が3以上の奇数の部分木を完成させる。
2つ以上の、子を含む部分木の頂点数が奇数であるような子について、その両方からの辺を残す。

である。こうならないような辺の取り除き方を数えていく。

DPの変数として、ある頂点 $i$ 以下の辺の取り除き方の総数であって、 $i$ 以下のグラフが正当であり、頂点 $i$ を含む部分木の頂点数が

1であるもの： $dp_{1}\lbrack i \rbrack$
2以上の偶数であるもの： $dp_{2}\lbrack i \rbrack$
3以上の奇数であるもの： $dp_{3}\lbrack i \rbrack$

とする。先ほど見たようにこの3パターンで部分木の性質が違うため、分けて数える。

$dp_{1}\lbrack i \rbrack$ を求める

頂点 $i$ と子の辺を全て切るしかない。このとき、子が含まれる部分木の頂点数が3以上の奇数であってはいけないので、

$dp_{1}\lbrack i \rbrack = \Pi_{j} (dp_{1}\lbrack j \rbrack + dp_{2}\lbrack j \rbrack)$

となる。ここで $j$ は $i$ の子を示す（以下も同様）。

$dp_{3}\lbrack i \rbrack$ を求める

そのままでは数えづらいので、 $dp_{1}\lbrack i \rbrack$ と合わせて部分木の頂点の個数が奇数個になる場合を考える。

複数の子から奇数個の頂点を繋いでくることはできないため、子からは偶数個の頂点を繋ぐかまたは辺を切り、頂点 $i$ 自身と合わせて奇数個になるというパターンしかない。つまり各子について、

子が含まれる部分木の頂点数は偶数個であり、頂点 $i$ と辺を繋ぐ。
子が含まれる部分木の頂点数は偶数個であり、頂点 $i$ と辺を繋がない。
子が含まれる部分木の頂点数は1個であり、頂点 $i$ と辺を繋がない。

の3パターンのどれかを採用することができる。数式は

$dp_{1}\lbrack i \rbrack + dp_{3}\lbrack i \rbrack = \Pi_{j} (dp_{1}\lbrack j \rbrack + 2\times dp_{2}\lbrack j \rbrack)$

となる。先ほど $dp_{1}\lbrack i \rbrack$ は求めたので、 $dp_{3}\lbrack i \rbrack$ を求めることができる。

$dp_{2}\lbrack i \rbrack$ を求める

これが少し厄介。子のうちどれか1つから奇数個の頂点を繋ぎ、残りの子は繋がないか偶数個の頂点を繋ぎ、頂点 $i$ 自身と合わせて頂点数が偶数個になるパターンである。

どの子から奇数個の頂点を繋ぐかを全部考えるため、

$dp_{2} \lbrack i \rbrack = \sum_{j}\left((dp_{1}\lbrack j \rbrack + dp_{3}\lbrack j \rbrack) \times \Pi_{k\ne j}(dp_{1}\lbrack k \rbrack + 2\times dp_{2}\lbrack k \rbrack)\right)$

と複雑な式になる。これを真面目に計算しようとすると子の数の2乗オーダーがかかってしまうが、 $\Pi_{k\ne j}(\cdots)$ の計算について「全部掛け算したものを計算しておいて、 $j$ についてだけ逆元を掛ける」ようにすると1乗オーダーで計算できる。

仕上げ

このDPを根まで計算する。最後に根を含む部分木の頂点数が3以上の奇数になってはいけないため、根を $r$ とすると答えは $dp_{1} \lbrack r \rbrack + dp_{2} \lbrack r \rbrack$ のmodを取ったものである。

ACコード

ACコードとして2つリンクを貼る。

（0除算対策あり）Submission #45964352 - Codeforces
（0除算対策なし）Submission #45964650 - Codeforces

計算の途中で逆元を取るため、その値がmod計算後にちょうど0だった場合に危険である。十分大きい素数なので余りが0になる確率は非常に低く、意図的に0除算を誘うような入力を作るのもかなり難しいとは思われるが、ちゃんと解くなら対策をしておくほうがよい。ただ、実装がわりと面倒くさい。

リンクの通り、0除算対策をしないコードでもACは取れている。

さいごに

このように木DPで数え上げを行う問題として「Ribbons on Tree」や「Squirrel Migration」があり、これらの強烈なイメージがあったため今回の問題を自力で解くことができたと思う。

木DPは楽しい。

2018-11-19

CODE FESTIVAL 2018 Final (Parallel)　参加記録＆解説（A～F）

AtCoder プログラミング競技プログラミング

オープンコンテスト8位でした。

f:id:betrue12:20181118231936p:plain

A～Fについて書きます。この記事を書いている時点で解説が公開されていないため、Twitterなどで見た他の参加者さんの解法を大いに参考にしながら書いています。

A - 2540

解法

長さが $l$ と $2540-l$ の2本の辺で、ちょうど1つの端点を共有するペアを数えればよいです。ただし、重複しないように注意する必要があります。

私の方針は以下です。

頂点 $v$ と辺の長さ $l$ ごとに、「頂点 $v$ から伸びている長さ $l$ の辺の本数」をmapで管理する。
辺を1本ずつ見ていく。そのとき、
- その辺の端点それぞれについて、その時点でのmapを使ってこれ以前に見た辺のうちペアになるものの辺の本数を数える。
- その後、辺をmapに追加する。

このようにすると重複なく数えられます。

ACコード

B - Theme Color

解法

要求されている答え方が特殊ですが、まずは普通に確率の求め方を考えます。結論を書くと、求めたい確率は

$p = \frac{N!}{r_{1}! r_{2}! \cdots r_{M}!} (\frac{1}{M})^{N}$

になります。この計算は、 $M=2$ の場合は「反復試行の確率の公式といろいろな例題」に説明があり、これを「多項定理の例題と2通りの証明」に書かれている式のように $M\ge 3$ の場合に拡張したものです。

さて、求めたいのは $p \ge 10^{-x}$ を満たす最小の整数 $x$ です。指数の形を除去するため、両辺底が10の対数を取ります。対数を取ると積は和になるので、

$\log_{10}p = \log_{10}N! - (\log_{10}r_{1}! + \cdots + \log_{10}r_{M}!) - N\log_{10}M \ge -x$

という式になります。この式から求めたい整数 $x$ は

$x = \lceil -\log_{10}N! + (\log_{10}r_{1}! + \cdots + \log_{10}r_{M}!) + N\log_{10}M \rceil$

となるので、 $\log_{10}k!$ を $1 \le k \le N$ の範囲で前計算しておけば $x$ を計算できます。

ACコード

Rubyのコードは多項定理ではなく二項定理の組み合わせで書いているので少し無駄な計算が入っていますが、やっていることは同じです。

C - Telephone Charge

解法

制約が特殊です。それぞれのプランで、通話時間 $A_{i}$ の時に料金が他のプランより安くなるということは、グラフで描くと以下のような関係になっているはずです。

f:id:betrue12:20181119004253p:plain

色が各プラン、太線になっているところがその区間での最安のプランを示しています。このグラフから、例えば図中の $T_{i}$ の位置であれば、プラン3またはプラン2が最安になることがわかります。

解法としては、プランを $A_{i}$ の値でソートしておき、各 $T_{i}$ についてどの $A_{i}$ の間に位置するかを二分探索などで特定し、その2つ（端なら1つ）の値を両方試して安い方を採用すればよいです。

ACコード

D - Three Letters

解法

本番は解けませんでしたが…

文字列の中から文字列の並びを探す時に、文字種とインデックスのどちらでループを回すかによって計算量の見積もりが変わってきます。今回の場合、「1文字目と3文字目は文字種で、2文字目はインデックスで」という少しトリッキーな考え方が必要になります。

ある文字列 $A_{i}$ について、2文字目のインデックスを左から右にずらしていきます。このとき、「左側に各文字がそれぞれ何個あるか」「右側に各文字がそれぞれ何個あるか」は、累積和のように計算することができます。

f:id:betrue12:20181119194955p:plain

このようにすると、

2文字目は、文字のインデックス全てについて全探索（全文字列合わせて最大 $90000$ ）
その2文字目に対して、1文字目と3文字目を文字種全てについて全探索（ $52^{2}$ ）し、ともに1個以上あるかチェック

として、3文字の文字列の存在を判定することができます。

ただしこの数え方をそのまま行うと、ある $A_{i}$ に対して同じ文字列を重複して数えてしまう可能性があります。それを防ぐため、3文字の文字列パターン全てにおいて「その文字列が最後に発見されたのはどの $A_{i}$ か？」という値を管理しておきます。こうすると重複カウントを防ぐことができます。

※計算量について、単純計算すると $90000\times 52^{2} \simeq 2.4 \times 10^{8}$ となるので、これがもし想定解ならばかなり厳しい気がしています。ただコンテスト終了後のTwitterの書き込みを見た感じ、高速な言語を使ってこの解法で通した人が多そうです。

ACコード

（C++）Submission #3623170 - CODE FESTIVAL 2018 Final (Parallel)

実装においては、配列のインデックスなどに文字を使うためにアルファベット52文字を0～51の整数に変換しています。アルファベット大文字と小文字の間はASCIIコード上で連続していなかったりするので地味に注意です。

E - Tough Journey

解法

高橋くんが町 $i$ にいるとき、手持ちの水が合計何本になるように買うべきか考えます。もし距離 $K$ 以下の位置に今いる町よりも水の安い町がある場合、町 $i$ ではその町に行けるだけの水を買って、安いほうの町で新しく水を買うべきです。

そのため高橋くんが町 $i$ にいて、次に訪れる町 $i$ より水の安い町が町 $i+k$ であるとき、

$k \le K$ ならば、町 $i$ では手持ち $k$ 本になるように水を買う。
$k \gt K$ ならば、仕方がないので町 $i$ で上限の $K$ 本まで水を買う。

このように水を買うのが最適となります。

あとはこれを効率的に解く実装を考えればよいです。実装方法もいくつかあると思いますが、私の方針は

町を水の安い順にソートする。
セグメント木を用いて、ソートした町に対して以下を順番に行う。今考えている町をとして、
- それまで見てきた町から、 $i$ よりインデックスが大きいものの中で最もインデックスが小さいものを求める。
- 町 $i$ をセグメント木に追加する。

としました。具体的な実装はコードを参照してください。

ACコード

（C++）Submission #3611009 - CODE FESTIVAL 2018 Final (Parallel)

F - Dinner Planning

解法

まず単純に考えると、順番に食事をしていくことを仮定しながらグルメ度の変化を見ていって、

グルメ度が $K$ を超えてしまった場合、それまでに行ったレストランの中で最も美味しさが低いものをキャンセルする。
グルメ度が $0$ を下回ってしまった場合、それまでに行ったラーメン屋の中で最も美味しさが低いものをキャンセルする。

ということをしたくなります。

ただし、これでは困るケースが出てきます。例えば以下のグラフのように、「グルメ度が $K$ を超えたので過去のレストランをキャンセルしたら、そのせいでグルメ度が0未満になる日が出てしまった」というケースです。

f:id:betrue12:20181119202732p:plain

こうなっては困るので、キャンセルすべきは「最後にグルメ度が0になった日以降で、美味しさが最も低いレストラン」となります。グルメ度が0を下回った場合は全く逆のことをします。

※これを毎回貪欲に選んで大丈夫なのか？後々の選択と合わせるとより良い選び方があるのでは？という疑問が浮かびますが、ちゃんとやると証明できると思います。記述がかなり長くなりそうなのでここでは省略します…

ということで、求めたいのはそれまでのグルメ度の推移を全て計算しておき

最後にグルメ度が0（または $K$ ）になったのはいつか？
ある区間におけるレストラン（またはラーメン屋）で一番美味しさが低いのはどれか？

を求めることです。これだけならどちらもセグメント木を用いて求めることができます。グルメ度に関してはある日から現在までの区間最小値が0かどうか（または最大値が $K$ かどうか）で二分探索です。

ただしグルメ度に関してはそれに加えて「過去に遡って、食事をキャンセルした日以降のグルメ度を1変化させる」という操作が必要です。そのため区間に対する操作を行える遅延評価セグメント木を用いれば、必要な全ての操作が可能になって解くことができます。

ただ、これまた想定解ではなさそうですね…。

ACコード

Submission #3623458 - CODE FESTIVAL 2018 Final (Parallel)

2018-11-14

Educational Codeforces Round 54 参加記録＆解説（A～F）

Codeforces プログラミング競技プログラミング

Dashboard - Educational Codeforces Round 54 (Rated for Div. 2) - Codeforces

今回はなんと17位！…なんですが、本番中のD問題のジャッジに致命的なミスがあって正常なコンテストではなかったため、素直に喜べない感じです…

f:id:betrue12:20181113205852p:plain

6問振り返ります。

A. Minimizing the String

Problem - A - Codeforces

問題概要

英小文字 $n$ 文字からなる文字列 $s$ が与えられる。この文字列から最大1文字を取り除いてできる文字列のうち、辞書順最小のものを求めよ。

制約

$2 \le n \le 2\times 10^{5}$
$s$ は英小文字からなる

解法

文字列の $i$ 文字目よりも $i+1$ 文字目のほうが辞書順で小さいとき、 $i$ 文字目を取り除くことで元の文字列よりも辞書順で小さい文字列を得ることができます。

辞書順で小さくするためにはできるだけ前のほうの文字を改善したほうがよいため、前から文字列を順番に見ていって、最初に $i$ 文字目よりも $i+1$ 文字目のほうが辞書順で小さくなるところで $i$ 文字目を取り除くのが最適です。ただし、s = aaa や s = abcde など最後までそのような $i$ がない場合は最後の文字を取り除きます。

ACコード

Codeforces

B. Divisor Subtraction

Problem - B - Codeforces

問題概要

正整数 $n$ が与えられる。 $n = 0$ になるまで以下の操作を繰り返す時、その操作回数を求めよ。

$n$ から、「その時点での」 $n$ の最小の素因数を引く。

制約

$2 \le n \le 10^{10}$

解法

もし $n$ が偶数の場合、最小の素因数は2です。偶数 $n$ から2を引いてもやっぱり偶数なのでまた2を引き…を最後まで繰り返すので、操作回数は $\frac{n}{2}$ です。

もし $n$ が奇数の場合、最小の素因数を $p$ とするとこれは必ず奇数です。そのため1回目の操作で値は $n - p$ となり、これは奇数同士の差なので偶数です。あとは2を引き続けるため、合計の操作回数は $1 + \frac{n-p}{2}$ となります。

ACコード

Submission #45598676 - Codeforces

C. Meme Problem

Problem - C - Codeforces

問題概要

以下の問題を $t$ 回解け。

非負整数 $d$ が与えられる。非負の実数 $a, b$ であって $a+b = ab = d$ であるものが存在するか判定し、もし存在すればその値を求めよ。

制約

$1 \le t \le 10^{3}$
$1 \le d \le 10^{3}$

解法

連立方程式を解く常套手段として、片方の変数 $b$ を消去します。 $b = d-a$ を $ab = d$ に代入して整理すると $a^{2} - ad + d = 0$ となり、これは $a$ についての2次方程式なので解の公式を用いると $a = \frac{d \pm \sqrt{d^{2} - 4d}}{2}$ となります。

$a = \frac{d + \sqrt{d^{2} - 4d}}{2}, b = \frac{d - \sqrt{d^{2} - 4d}}{2}$ のとき実際に計算すると確かに $a + b = ab = d$ になっているため、この2つが非負の実数であれば答えになります。もちろん逆でもよいです。

まず実数である条件は $d^{2} - 4d \ge 0$ で、これが満たされない場合は条件を満たす $a, b$ が存在しません。またこの条件が満たされる時、 $d \ge \sqrt{d^{2} - 4d} \ge 0$ が成り立つことから $a, b$ はともに非負となるため、それぞれ計算して出力すればよいです。

ACコード

Codeforces

D. Edge Deletion

Problem - D - Codeforces

問題概要

$n$ 頂点 $m$ 辺の重み付き単純連結無向グラフと、整数 $k$ が与えられる。辺 $i$ の重み（長さ）は $w_{i}$ である。このグラフにおける頂点1から頂点 $i$ までの最短路の長さを $d_{i}$ とする。

このグラフから $k$ 本以下の辺を残す方法の中で、「残した辺だけを使った頂点1から頂点 $i$ までの最短路を求めた際に、その長さが変わらず $d_{i}$ となるような頂点 $i$ の個数」が最大となるような残し方を1つ求めよ。

制約

$2 \le n \le 3 \times 10^{5}$
$n-1 \le m \le 3 \times 10^{5}$
$0 \le k \le m$
$1 \le w_{i} \le 10^{9}$
グラフは重み付き単純連結無向グラフ

解法

頂点1から各頂点への最短距離はダイクストラ法で求めることができます。このとき、一緒に「各頂点への最短路に使う辺」も調べることができます。全ての頂点に対する最短路に使う辺を集めると、これは「最短経路木」と呼ばれる木になります。

※1つの頂点への最短路として長さが同じ複数の経路がある場合は、ちゃんと木になるよう経路を適切に選ぶ必要がありますが、よくあるダイクストラ法の実装のように「新しい経路の長さが、それまでに見つかった最も短い経路より真に短い場合だけ経路を更新する」という実装をしておけば大丈夫です。

辺を全て取り除いた状態から、1本ずつ辺を足していくことを考えます。このとき頂点1からの連結性を保ったまま、先ほどの最短経路木に含まれる辺だけを足していくと、新しく連結になった頂点へは頂点1から最短路を辿って到達することができます。このようにして辺を $k$ 本まで（または、全域木となる $n-1$ 本まで）足していけばそれが答えとなります。

ACコード

Submission #45615172 - Codeforces

ダイクストラ法において最短路の復元を行う場合、始点以外の頂点それぞれについて「最短路における、1つ前の頂点」を記録しておくのが常套手段です。ただし今回は辺の番号のほうが後々使いやすいため、代わりに1つ前の頂点からの辺番号を記録しています。

E. Vasya and a Tree

Problem - E - Codeforces

問題概要

頂点1を根とする $n$ 頂点の根付き木が与えられる。各頂点には値が書かれていて、初期値は全て0である。

頂点 $x$ の $k$ -subtreeを、頂点 $x$ の子孫（自身を含む）であり $x$ との距離が $k$ 以下である頂点の集合と定義する。以下のクエリが $m$ 個与えられる。

整数 $v_{i}, d_{i}, x_{i}$ が与えられる。頂点 $v_{i}$ の $d_{i}$ -subtreeに含まれる全ての頂点の値に $x_{i}$ を加算する。

クエリを全て処理した後の、各頂点に書かれている値を求めよ。

制約

$1 \le n \le 3\times 10^{5}$
与えられるクラフは木
$1 \le m \le 3 \times 10^{5}$
各クエリについて、
- $1 \le v_{i} \le n$
- $0 \le d_{i} \le 10^{9}$
- $1 \le x_{i} \le 10^{9}$

解法

各クエリを独立に処理し、影響を受ける全部の頂点にいちいち値を足していては間に合いません。効率的な計算方法を考えます。

頂点 $v_{i}$ の根からの深さを $D_{i}$ とします。するとクエリ $i$ で値が足されるのは、 $v_{i}$ の子孫であって深さが閉区間 $\lbrack D_{i}, D_{i}+d_{i}\rbrack$ に含まれる頂点であると表現することができます。範囲について値を足すクエリを大量に処理する方法として、「いもす法」のようなことができないか考えてみます。

普通のいもす法と比べるとかなり変則的ですが、以下のような方法を考えます。このようにすると、根から頂点をDFSしつつ、足される値の合計を差分更新することができます。

スライド最終ページにも書きましたが、いもす法を用いるメリットは「範囲に対する多数のクエリをまとめて処理できる」ことです。最初にクエリを全て読み込んで $v_{i}$ ごとに振り分けておけば、スライドで示したようなDFSで同時並行的にクエリを処理しながら全頂点の値を求めることができます。

ACコード

Submission #45682359 - Codeforces

F. Summer Practice Report

Problem - F - Codeforces

問題概要

$n$ ページのレポートがあり、 $i$ ページ目には $x_{i}$ 個の表と $y_{i}$ 個の数式を好きな順序で一列に並べて書く。このとき、ページをまたいで連続するものも含めて、表だけ・または数式だけが連続して $k+1$ 個以上続いてはいけない。そのような並べ方は可能かどうか判定せよ。

制約

$1 \le n \le 3\times 10^{5}$
$1 \le k \le 10^{6}$
$1 \le x_{i} \le 10^{6}$
$1 \le y_{i} \le 10^{6}$

解法

表だけ・または数式だけが連続して $k+1$ 個以上続かないような並べ方を、正当な並べ方と呼ぶことにします。

ページの境目の扱いがやっかいなので、ここを上手く扱うことができないか考えます。ページの最後には表か数式のどちらかが書かれていますが、同じものが連続することを避けるためには「ページの最後に書かれている表/数式が、そのページの最後でいくつ連続で続いているか」の値をなるべく小さくしたいです。もちろん、1個であれば最も理想的です。

そこで、各ページ $i$ について

$i$ ページ目までの並べ方が正当であり、 $i$ ページ目の最後が表であるとき、その連続個数を最小でいくつにできるか？
$i$ ページ目までの並べ方が正当であり、 $i$ ページ目の最後が数式であるとき、その連続個数を最小でいくつにできるか？

をそれぞれ計算します。これをそれぞれ $X_{i}, Y_{i}$ とおくと、それらの値を使って次のページの値 $X_{i+1}, Y_{i+1}$ が計算できます。これを最後のページまで続けて、途中で $X_{i} \gt k$ かつ $Y_{i} \gt k$ となってしまうページが出てしまったら答えは「不可能」ですし、最後のページまでそうならなければ「可能」です。

ということで遷移を考えます。（注目するページを $i$ にしたいので、1つ添字をずらして $X_{i-1}, Y_{i-1}$ から $X_{i}, Y_{i}$ への遷移を考えることにします。）

以降、表が連続でいくつか並んでいる塊を X 、数式の塊を Y と表記します。 $i$ ページ目の表と数式の並べ方として、以下の4パターンを考えることができます。

XYXY......XY
XYXY......XYX
YXYX......YX
YXYX......YXY

すなわち、最初が X/Y どちらか、最後が X/Y どちらか、の4パターンです。

ここで、例えば最初が X である2パターンを考えます。最初の X の中にある表は、最大でいくつまで並べられるでしょうか？ページをまたいで表が $k+1$ 個以上連続してはいけないので、この値は $X_{i-1}, Y_{i-1}$ に依存しています。

$Y_{i-1} \le k$ であるとき、前ページの最後が Y である並べ方が可能であるため、それを採用すれば最初の X は $k$ 個並べられる。
であるとき、前ページの最後を Y にはできない。そのため、
- $X_{i-1} \lt k$ であるとき、最初の X は $k - X_{i-1}$ 個並べられる。
- $X_{i-1} \ge k$ であるとき、最初に X を置くことはできない。

このようにして、最初の X にいくつまで表を並べられるかを求めることができます。

それでは具体的に $X_{i}, Y_{i}$ を求めていきます。4パターンのうち XYXY....XY を使って求め方を説明します。残りのパターンも同様に考えることができます。

連続する同じ要素を減らしたいので、要素をばらけさせる、つまり X Y の塊をなるべく多くしたいです。このパターンでは X と Y の個数が等しいため、それぞれの塊の個数は最大で $\min(x_{i}, y_{i})$ 個まで増やすことができます。この値を $m$ と置きます。

塊がそれぞれ $m$ 個のときに

$x_{i}$ 個の表を、（最初の X に置ける個数を考慮して）それぞれの塊に含まれる要素数が $k$ を超えないように $m$ 個の X に分配できるか？
$y_{i}$ 個の数式を、それぞれの塊に含まれる要素数が $k$ を超えないように $m$ 個の Y に分配できるか？またそのとき、一番右の Y に含まれる数式は最小でいくつにできるか？

を計算します。実際に並べてみたものが以下の図です。

f:id:betrue12:20181114214859p:plain

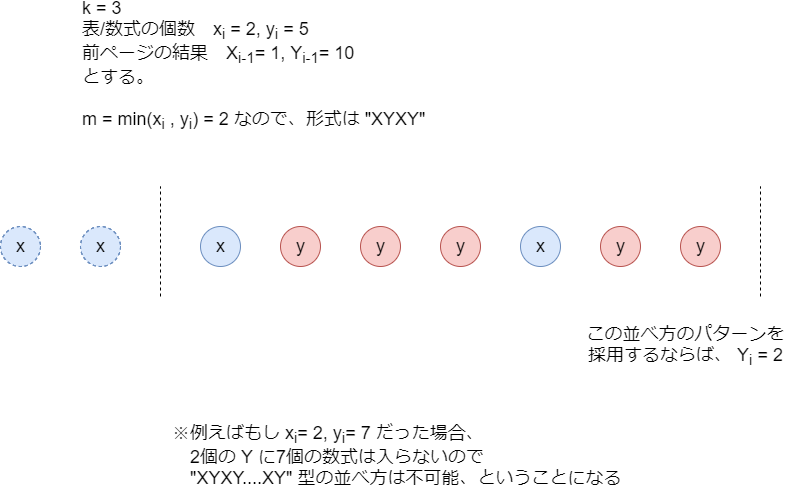
具体的には、先ほど求めた「最初の X に最大でいくつまで表を並べられるか」を $a$ として

$a + (m-1)k \ge x_{i}$ のとき、表を X に正当に分配できる。
一番右の Y に含まれる数式の最小個数は $\max(1, y_{i} - (m-1)k)$ であり、その値が $k$ 以下であれば数式を Y に正当に分配できる。

という結果になります。

このようにパターンを4つ試して、

XYXY......XY と YXYX......YXY のうち、「正当な並べ方」を実現できて、かつ一番右の Y に含まれる数式の個数が少ない方を $Y_{i}$ とする
XYXY......XYX と YXYX......YX のうち、「正当な並べ方」を実現できて、かつ一番右の X に含まれる表の個数が少ない方を $X_{i}$ とする

ことで遷移が求められます。これをバグらせずに全パターン実装するのはなかなか神経を使いますが、結果的には $O(n)$ で解くことができます。

ACコード

Submission #45627726 - Codeforces

私の実装の癖もあって、上の説明とは変数名がかなりずれています…すみません。適宜読み替えてください。

2018-11-04

ABC113 参加記録＆解説

AtCoder プログラミング競技プログラミング

AtCoder Beginner Contest 113 - AtCoder

22分台全完で21位でした。

f:id:betrue12:20181104225338p:plain

A - Discount Fare

解法

$X + \frac{Y}{2}$ を計算して出力すればよいです。

ACコード

（Ruby）Submission #3531033 - AtCoder Beginner Contest 113

B - Palace

解法

$N$ 個の地点それぞれについて $|(T - H_{i} \times 0.006) - A|$ を計算し、それが最も小さい地点を探せばよいです。

ACコード

ちょっとした実装テクとして、上記のコードのようにC++の min_element を使うと、「 vector の中で最も小さい要素のインデックス」がスマートに取得できます。

C - ID

解法

市を県ごとに分類し、それぞれの県ごとに誕生年でソートします。そうすると、それぞれの市がその県で何番目に誕生した市かが分かります。

…というものを素直に実装すればよいです。300点問題で数学が要らないのは、最近だと珍しいですね…

ACコード

実装テクという点では、

誕生年でのソートをする際に、市のインデックスも巻き込むと後の実装がしやすくなる。そのため市を県ごとに分類する際、C++だと pair などを使って、誕生年と市のインデックスをまとめておく。
指定された桁数になるように左に0を埋める方法（C/C++だと、printf のフォーマット指定子で可能）

などを知っておくとよいですね。

D - Number of Amidakuji

解法

ある行までの横線の引き方は、その1つ上の行までの横線の引き方から計算できそうです。上からDPをしていくことを考えます。

「 $i$ 行目まで考えた時に、縦線1からスタートしたものが $k$ 番目の縦線に移動しているような横線の引き方の総数」を $dp\lbrack i \rbrack\lbrack k \rbrack$ とします。初期条件は $dp\lbrack 0 \rbrack\lbrack 1 \rbrack = 1$ で、答えは $dp\lbrack H \rbrack\lbrack K \rbrack$ です。

$i$ 行目から $i+1$ 行目への遷移に必要な情報は、「1行の横線の引き方であって、 $j$ 番目の縦線から $k$ 番目の縦線に移動する引き方の総数」です。これを $num\lbrack j \rbrack\lbrack k \rbrack$ とすると、 $i$ 行目から $i+1$ 行目の遷移は

$dp\lbrack i+1 \rbrack\lbrack k \rbrack = \sum_{j} (dp\lbrack i \rbrack\lbrack j \rbrack \times num\lbrack j \rbrack\lbrack k \rbrack)$

と求められます。

次は、この $num\lbrack j \rbrack\lbrack k \rbrack$ の求め方を考えます。1行の横線の引き方は、線を引くところが $W-1$ 箇所しかないため、高々 $2^{W-1}$ 通りです。 $W \le 8$ であることから $2^{W-1}$ は十分小さいので、全部確認してしまいましょう。

f:id:betrue12:20181104234145p:plain

1行の線の引き方を全部列挙すれば、以下のように $num\lbrack j \rbrack\lbrack k \rbrack$ が求められます。

0から $2^{W-1} -1$ までの整数をループで回す。この整数をビット列として見た時の $W-1$ 個のビットがそれぞれ横線の有無を表し、 $k$ 番目のビットが1であることは「 $k, k+1$ 本目の縦線間に横線がある」ことを示す。
これが「どの2つの横棒も端点を共有しない」というルールに違反する、つまりビット列として見た時に連続した1を含む場合、スキップする。
この線の引き方のとき、 $j$ 番目の縦線からどこの縦線に移動するかを各 $j$ ごとに計算する。これを $k_{j}$ とおく。
各 $j$ ごとに、 $num\lbrack j \rbrack\lbrack k_{j} \rbrack$ に1を加算する。

この $num\lbrack j \rbrack\lbrack k \rbrack$ を用いてDPを行えば、答えを求めることができます。

ACコード

2018-10-26

Educational Codeforces Round 53 参加記録＆解説（A～D）

Codeforces プログラミング競技プログラミング

Dashboard - Educational Codeforces Round 53 (Rated for Div. 2) - Codeforces

4完で256位。キリ番です（？）

Div2オンリーならもっと上を目指したいところ…

f:id:betrue12:20181026194348p:plain

A. Diverse Substring

Problem - A - Codeforces

問題概要

長さ $n$ の英小文字列 $s$ が与えられる。 $s$ の連続部分文字列 $s^{\prime}$ であって、以下の条件を満たすものを1つ求めよ。あるいはそれが存在しないことを判定せよ。

$s^{\prime}$ に含まれるどのアルファベットも、それが $s^{\prime}$ に含まれる個数は $\frac{|s^{\prime}|}{2}$ を超えない。

制約

$1 \le n \le 1000$
$s$ は英小文字からなる

解法

$\frac{|s^{\prime}|}{2}$ を「超えない」ということは、ちょうど半分はOKということです。なので、隣接する2文字が異なる箇所が $s$ に存在すれば、その2文字は答えになります。

もし隣接する2文字が異なる箇所がない場合、全ての文字が同じだということなので、その場合答えは存在しません。

ACコード

（C++）Submission #44846895 - Codeforces

B. Vasya and Books

Problem - B - Codeforces

問題概要

$n$ 冊の本が積み上げられている。上にあるものから順に、相異なる $a_{1}, ..., a_{n}$ の番号が付いている。

以下の操作を $n$ 回行う。

取り出したい本の番号が与えられる。この番号は操作ごとに相異なる。
- その本が積み上げられた本の中に存在する場合、その本とその本より上にある本を全て取り出す。
- その本がもう取り出し済みである場合、何もしない。

各操作において取り出される本の数を求めよ。

制約

$1 \le 2\times 10^{5}$
$1 \le a_{i} \le n$ であり、これらは相異なる
$1 \le b_{i} \le n$ であり、これらは相異なる

解法

$a_{i}$ は「上から $i$ 番目の本の番号はいくつか」という情報ですが、これを「番号 $j$ の本は上から何番目にあるか」という情報に変換しておきます。

各操作を処理する際には、今まで上から何冊の本を取り出したかを記憶しておきます。本の番号 $b_{i}$ からその本の位置が分かれば、追加で何冊本を取り出さなければいけないかが求められます。

ACコード

（C++）Submission #44851092 - Codeforces

C. Vasya and Robot

Problem - C - Codeforces

問題概要

座標平面にロボットがいる。初期位置は $(0, 0)$ 、目的地は $(x, y)$ である。

ロボットの動く方向（UDLR）を示す $n$ 文字の文字列 $s$ が与えられる。この文字列に以下のような変更をして、 $n$ 回の動作完了後にちょうどロボットが目的地にいるようにしたい。

$s$ の0文字以上の連続部分文字列を選択する。その中の文字それぞれを UDLR のうち好きなものに変更する（変更しない文字があってもよい）。

選択する連続部分文字列の長さを最小にしたい。その長さを求めよ。（どうやっても目的地にたどり着けない場合はそれを判定せよ）

制約

$1 \le n \le 2\times 10^{5}$
$s$ の各文字は UDLR のいずれかである
$-10^{9} \le x, y \le 10^{9}$

解法

まず、目的地に到達不可能である条件を考えます。 $d = |x| + |y|$ として、

$d > n$ である（届かない）
$d$ と $n$ の偶奇が異なる（ぴったり止まれない）

のどちらかを満たす時、到達不可能です。以降、到達可能である場合を考えます。

「連続部分文字列を選んでその中を変更する」ということは、裏返すと「左から○文字と、右から○文字は変更しない」ということです。どちらかの「変更しない文字数」を固定してみます。

「左から $i$ 文字目までを変更しないと決めた時、 $i+1$ 文字目から何文字目までを変更すれば目的地に到達可能か？」という問題を考え、その最小値を $j$ とします。そうすると $i$ が増加するにつれて $j$ も（広義）単調増加するため、しゃくとり法を使うことができます。

可能/不可能の判定においては、「変更しないと決めた文字だけでどこまで移動するか」を計算して、その到達点から目的地までの距離を計算します。自由に変更できる文字数がその距離以上であれば、（偶奇の判定は済ませているので）目的地に到達可能です。

しゃくとり法を行う上で必要な「区間に含める」「区間から除く」操作も、「変更しないと決めた文字でどれだけ移動するか」を1文字分足し引きすればよいので可能です。

ACコード

（C++）Codeforces

D. Berland Fair

Problem - D - Codeforces

問題概要

$n$ 軒の店が円形に並んでいて、 $i$ 番目の店はキャンディを1個 $a_{i}$ 円で売っている。

ポリカープは最初に $T$ 円持っており、以下のようにキャンディを買う。

1番目の店から順番に訪れる。
訪れた店で、キャンディを1個買うお金があれば1個買う。その後、次の店に移動する。（ $n$ 番目の次は1番目に移動する）
どの店でもキャンディを買えなくなったら終了する。

ポリカープが買うキャンディの個数を求めよ。

※お金の単位は勝手に円にしました。burlesってどこのお金の単位なんでしょうね…？

制約

$1 \le n \le 2\times 10^{5}$
$1 \le T \le 10^{18}$
$1 \le a_{i} \le 10^{9}$

解法

この問題はいろいろ解法があるみたいですが…私が解いたときのものを書きます。ちょっと面倒ですが、計算量の見積もりは楽です。

まず最初の状態において「全ての店でキャンディを購入する周回を何周できるか？」を考えます。全ての店のキャンディの価格合計を $A$ とします。 $T \ge A$ であるとき、 $k = \lfloor\frac{T}{A}\rfloor$ として全ての店のキャンディを $k$ 個買うことができます。所持金は $kA$ 円減り、キャンディを $kn$ 個入手し、1番目の店に戻ってきます。

その後、次の周回でキャンディを買おうとすると、どこかの店でキャンディを買えなくなります。所持金が増えることはないので、その店では今後1つもキャンディを買えず、通過するだけになります。そのため、この店を消してしまうことを考えます。

店を1つ消すと、1周あたりのキャンディの価格合計が減り、キャンディの個数も減ります。その状態で改めて「全ての店でキャンディを購入する周回を何周できるか？」を考えることができます。これを全てのお店が消えるまで繰り返すことで、答えを求めることができます。

この解法において必要なのは「どの店でキャンディを買えなくなるか」を判定することと、「その店を消す」ことの2つです。これはすなわち、

操作途中の所持金 $t$ について、 $t > a_{1} + \cdots + a_{i}$ となる最小の $i$ を求める。
ある要素 $a_{i}$ の値を0にする。

の2つの操作であり、これはBITでデータを保持し二分探索を行うことで実現できます。

BITでの二分探索は、毎回独立に合計クエリを処理していると全体計算量が $O(n\log^{2} n)$ になりますが、上手くやると $O(n\log n)$ にできます。今回の制約だと $O(n\log^{2} n)$ で十分間に合いました。

ACコード

（C++）Submission #44869480 - Codeforces

本番コード。これは $O(n\log^{2} n)$ です。

（C++）Submission #44911558 - Codeforces

$O(n\log n)$ も書いてみました。

最初に考えたこと

スキル上げフェーズとひたすら稼ぎフェーズ

美味しい依頼はスキルよりも優先

スキル上げ順番の操作

振り返り

さいごに

各オンラインジャッジのRuby環境

入出力編

数値編

負の数を含む剰余計算

浮動小数の出力

1e9のようなリテラル表記

ビット演算

最小公倍数、最大公約数

素数関連

配列編

要素の追加/削除にはなるべく破壊的操作を使う

配列のmax/minよりifや三項演算子を使う

負のインデックス

配列の要素の合計

二分探索

スコープ編

定数

おわり

問題概要

制約

解法

木の最大マッチングが一意に定まる条件

木DPをする

を求める

を求める

を求める

仕上げ

ACコード

さいごに

A - 2540

解法

ACコード

B - Theme Color

解法

ACコード

C - Telephone Charge

解法

ACコード

D - Three Letters

解法

ACコード

E - Tough Journey

解法

ACコード

F - Dinner Planning

解法

ACコード

A. Minimizing the String

問題概要

制約

解法

ACコード

B. Divisor Subtraction

問題概要

制約

解法

ACコード

C. Meme Problem

問題概要

制約

解法

ACコード

D. Edge Deletion

問題概要

制約

解法

ACコード

E. Vasya and a Tree

問題概要

制約

解法

ACコード

F. Summer Practice Report

問題概要

配列の`max/min`より`if`や三項演算子を使う

$dp_{1}\lbrack i \rbrack$ を求める

$dp_{3}\lbrack i \rbrack$ を求める

$dp_{2}\lbrack i \rbrack$ を求める