Educational Codeforces Round 49 参加記録

Dashboard - Educational Codeforces Round 49 (Rated for Div. 2) - Codeforces

前回に続き、今回もシステス落ち…

Aがシステスで落ちてBCDの3完。簡単な問題が落ちるとペナルティが重いです。

f:id:betrue12:20180819181738p:plain

本番中取り組んでいたEも含めて5問振り返っていきます。

A. Palindromic Twist

Problem - A - Codeforces

偶数個のアルファベット小文字からなる文字列 $s$ が与えられます。その文字それぞれに対して、「アルファベットを前か後ろに1つずらす」という操作を必ず1回ずつ行うことで、 $s$ を回文にできるか判定しなさい、という問題。

2個の文字を前か後ろに1つずつずらすことで一致させることできる条件は、「同じ文字であること」「ずらす時の距離が±2であること」のいずれかを満たすことです。整数に変換して差を取ります。

ACコード：Submission #41820490 - Codeforces

本番ではなぜかaとzがループするものだと思っていてコードを書き、システスで落ちました…

B. Numbers on the Chessboard

Problem - B - Codeforces

$n \times n$ の盤面に、以下のように番号が振られています。

まず、座標 $(x, y)$ の和が偶数になる点にだけ、左上から右下に順に番号を振る。このような点の数は $\lceil\frac{n^{2}}{2}\rceil$ 個である。
続けて、残りの点に左上から右下に番号を振る。

与えられた座標に書かれている値を答えなさい、という問題。

ちまちまと計算していけば良いのですが実装が面倒で、特に $n$ が奇数の時が厄介です。コードの方針としては、

座標和が奇数であれば、まず $\lceil\frac{n^{2}}{2}\rceil$ を加算する。これは座標和が偶数のマスに割り当てられている数字の数。これ以降は、座標和の偶奇が自分と同じマスだけ考えればよい。
自分より上にある行を2で割った数 $\times N$ を加算する。座標和が偶数であっても奇数であっても、 $n$ が偶数であっても奇数であっても、隣り合う2行で消費する数字の個数は $N$ であるため。
自分より上にある行数が奇数なら、2. で足されていない1行が余っているので、その個数を加算する。
自分の行で、自分自身とその左にある要素の個数を加算する。

f:id:betrue12:20180819114850p:plain

これを実装し、問題文中にある $4 \times 4$ と $5 \times 5$ の全マスを出力させて正しいことを確認してからsubmitしました…。

ACコード：Submission #41764843 - Codeforces

C. Minimum Value Rectangle

Problem - C - Codeforces

与えられた棒の中から4本使ってできる長方形のうち、周の長さ $P$ 、面積 $S$ として $\frac{P^{2}}{S}$ が最小になるものを見つけなさい、という問題。

まず、辺として使える長さの候補について考えます。長方形を作るには、同じ長さの棒が2ペア必要です。4本あれば正方形が作れます。ソートして前から見るか、map等で各長さの棒の本数を数えていけば列挙できます。

長方形の隣り合う辺の長さを $a, b$ とすると、 $P = 2(a+b), S = ab$ であるため、評価式は $\frac{P^{2}}{S} = \frac{4(a+b)^{2}}{ab}$ となります。この分子・分母の関係は相加・相乗平均の関係に似ていて、 $a = b$ の時16で最小値を取ります。直感的には、 $a, b$ がなるべく近い値であればよさそうです。

そのため、辺として使える候補をソートし、隣り合うものを全部試すことを考えます。隣り合うものを使わない場合は結果が悪くなることが、不等式を使って頑張れば示せます*1。全部試して一番評価式が小さいものを出力します。

独立な複数の問題が1つのテストケースにまとまっているので計算量の評価が難しいですが、それぞれの問題は棒の数 $n$ に対して $O(n \log n)$ （ソートの計算量）で解けて、全問題の棒の数の総和を $N$ とすると $N = \sum n \le 10^{6}$ であることを考えると、 $O(N \log N)$ で全体計算量が抑えられると思います。

まあRubyではTLEしましたが…

ACコード：Submission #41772412 - Codeforces

D. Mouse Hunt

Problem - D - Codeforces

$n$ 個の部屋それぞれにネズミが出没し、各部屋について「その部屋に来たネズミは次にどの部屋に行くか」を示す $a_{i}$ が設定されています（ $a_{i} = i$ の時はその部屋に留まり続けます）。また各部屋に、ネズミ取りを置くためのコスト $c_{i}$ が設定されています。

「どの部屋にネズミが出ても、必ずどこかで捕まえられる」という条件を満たすために必要な最小コストを求めてください、という問題。

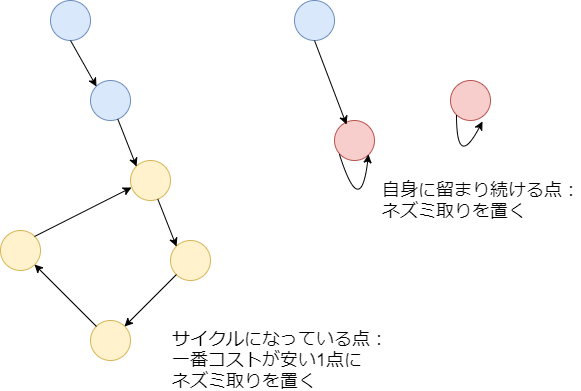
ネズミの移動を追っていくと、どの部屋から出発しても最終的には以下のいずれかになります。

$a_{i} = i$ であるいずれかの部屋に留まり続ける。
循環するサイクルになっている複数の部屋を無限に周り続ける。

そのため、この最終地点にネズミ取りを仕掛けるのが効率が良いです。 $a_{i} = i$ である部屋にネズミ取りを仕掛け、サイクルになっている場合はその中で一番コストが安い部屋1つにネズミ取りを仕掛けます。それ以外の部屋からスタートしたネズミも、最終的には必ずこれらのいずれかの部屋に来るため、捕まえられます。

f:id:betrue12:20180819121857p:plain

というわけでグラフを作ります。サイクルを潰したいので、ちょっとオーバーキルな気もしますが強連結成分分解を使います。ライブラリ持ってたし。

方針として、

部屋を頂点、ネズミの移動を辺とする有向グラフを作る。
強連結成分分解でサイクルを潰し、「サイクル内の点の中で一番安いコスト」を持つ点とみなす。
サイクルのない有向グラフ（DAG）になったので、移動の終端となる、つまり出次数が0である点のコストを合計する。

これで解けます。

ACコード：Submission #41779227 - Codeforces

E. Inverse Coloring

Problem - E - Codeforces

$n \times n$ の盤面に白または黒のタイルを貼ります。以下の条件を満たすタイルの貼り方を数え上げなさい、という問題。

$i+1$ 行目のタイルの貼り方は、 $i$ 行目と全く同じか、またはそれを白黒反転させたものである。
列についても、同様の条件を満たす。
同じ色のタイルで構成される長方形の面積は $K$ 未満である。*2

長方形の面積は隣り合う2辺を $a, b$ として $a \times b$ なので、「同じ色が横に何連続しているか」「縦に何連続しているか」を気にしながら数え上げていくことを考えます。

f:id:betrue12:20180819143841p:plain

まず、1行目のタイルの貼り方を数え上げます。このとき、「同じ色が横に最大で何連続しているか」ごとに区別して数え上げていきます。この値を $a$ としておきます。

そのタイル1行について、2行目以降は「反転する」「反転しない」の分岐で数えていくことができます…が、「反転しない」を連続で選び続けると縦に同じ色が連続してしまい、面積の条件を破ってしまいます。具体的には反転しない連続回数を $b$ とすると、 $a \times b \lt K$ を満たす範囲に $b$ を収める必要があります。

数え上げ方針が立ったので、DPを考えていきます。1行目の貼り方は、「 $i$ 枚目まで見て、これまでの最大連続回数が $j$ で、今見ているところまでの連続回数が $k$ である貼り方」をテーブルに持って $O(N^{3})$ のDPができます。それを $i=N$ まで見た時の値が、「横に最大で $j$ 連続している1行目のタイルの貼り方」になります（ $k$ の区別はもう要らないので合算しちゃいましょう）。

そこから、「 $i$ 行目まで積んで、横に最大で $j$ 連続していて、今見ているところまでの縦の連続回数が $k$ であるタイルの貼り方」をテーブルに持つDPをします。これも同様に $O(N^{3})$ です。ただし $j \times k \lt K$ を満たさないような値については加算しません。これで答えが求まります*3。

さてこれを実装してサンプルも確認して提出したものの… $501^{3}$ の配列が大きすぎてコンパイルエラー。どのみちコンパイルが通ったとしてもMLEなので、メモリ節約のため2次元配列を使い回すように書き換えると今度はTLE。コンテスト中はそれで終わってしまいましたが、そこからさらに不要なループ範囲を削って定数倍の高速化をすれば通すことができました。