ARC099 参加記録(WIP)
AtCoder Regular Contest 099 - AtCoder
今回は26分台1完で685位、ダメダメな結果でした…

レートも大きく下がり、水色に戻ってしまいました。次頑張ります。
CとDの2問を振り返っていきます。
C - Minimization
「最初,この数列の要素は を並び替えたものになっています.」 という記載が重要で、これを見落とすと無駄に難しい問題を解くハメになります。(1敗)
「選んだ範囲内の値をその中の最小値で置き換える」という操作で全ての要素を等しくしたいので、最終状態では全ての要素が全体の最小値、つまり1になります。そして上記の条件から、初期状態では1が存在するのは1箇所だけです。
そのため、問題は以下のように単純化できます。
- 初期状態では1が1つだけ
- 1を含む幅
の範囲を選択することで、その範囲の数値を全て1にできる
- 全ての要素を1にするために必要な操作は何回か?
具体的には最初に1を含む範囲を取って、そこから広げていくような操作になりますが、最初の範囲の取り方を間違えるとムダが出てしまいます。少し発想を変えて、「隣同士で共有部分を持ちつつ、全体をムダなく覆う範囲の取り方」 を考えます。
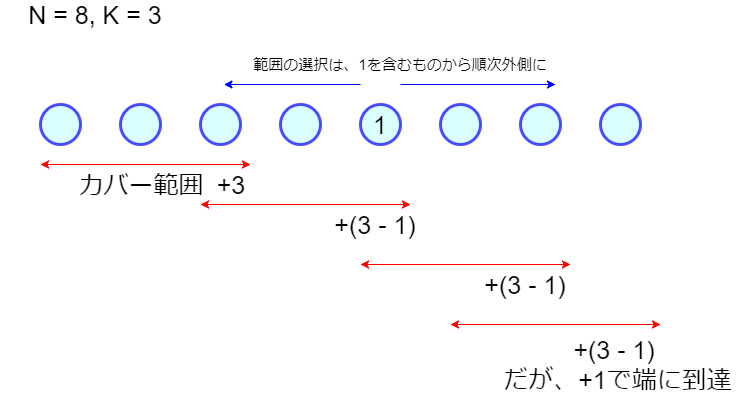
この範囲たちを最初に全部決めてから、1が含まれているものから順に選んでいけば、最小の範囲数で全体を1にできます。共有部分*1があることを考慮すると、1つ目の範囲では 、2つ目以降の範囲では
だけカバー可能な数が増えていくので、その合計が
に到達するのに必要な範囲数を求めればよいです。
スマートなACコード:Submission #2739168 - AtCoder Regular Contest 099
一応、最小値が1つだけという条件を見落としても解けないことはないです…
問題文を見落としたACコード:Submission #2722704 - AtCoder Regular Contest 099
D - Snuke Numbers
本番中には解けませんでしたが…
すぬけ数がどんな形になるのか直感的に分かりづらいのと、サンプルの情報がとても少ないので、まずは値が小さい範囲で実験してみます*2。
Snuke Numbers実験用スクリプト · GitHub
最後のほうの値は正確ではないので一部切っています。すぬけ数のおおよその形を掴むことができます。
[1, 2, 3, 4, 5, 6, 7, 8, 9, 19, 29, 39, 49, 59, 69, 79, 89, 99, 199, 299, 399, 499, 599, 699, 799, 899, 999, 1099, 1199, 1299, 1399, 1499, 1599, 1699, 1799, 1899, 1999, 2999, 3999, 4999, 5999, 6999, 7999, 8999, 9999, 10999, 11999, 12999, 13999, 14999, 15999, 16999, 17999, 18999, 19999, 20999, 21999, 22999, 23999, 24999, 25999, 26999, 27999, 28999, 29999, 39999, 49999, 59999, 69999, 79999, 89999, 99999, 109999, 119999, 129999, 139999, 149999, 159999, 169999, 179999, 189999, 199999, 209999, 219999, 229999, 239999, 249999, 259999, 269999, 279999, 289999, 299999, 309999, 319999, 329999, 339999, 349999, 359999, 369999, 379999, 389999, 399999, 499999, 599999, 699999, 799999, 899999, 999999, 1099999, 1199999, 1299999, 1399999, 1499999, 1599999, 1699999, 1799999, 1899999, 1999999, 2099999, 2199999, 2299999, 2399999, 2499999, 2599999, 2699999, 2799999, 2899999, 2999999, 3099999, 3199999, 3299999, 3399999, 3499999, 3599999, 3699999, 3799999, 3899999, 3999999, 4099999, 4199999, 4299999, 4399999, 4499999, 4599999, 4699999, 4799999, 4899999, 4999999, 5999999, 6999999, 7999999, 8999999, 9999999, 10999999, 11999999, 12999999, 13999999, 14999999, 15999999, 16999999, 17999999, 18999999, 19999999, 20999999, 21999999, 22999999, 23999999, 24999999, 25999999, 26999999, 27999999, 28999999, 29999999, 30999999, 31999999, 32999999, 33999999, 34999999, 35999999, 36999999, 37999999, 38999999, 39999999, 40999999, 41999999, 42999999, 43999999, 44999999, 45999999, 46999999, 47999999, 48999999, 49999999, 50999999, 51999999, 52999999, 53999999, 54999999, 55999999, 56999999, 57999999, 58999999, 59999999, 69999999, 79999999, 89999999, 99999999]
この数列から、以下のようなことが観察できます。
- 2桁以上の数は、末尾が9で埋まっている
- どのくらい9で埋まっているかは固定されていないように見える(1099はあるけど、2099はない)
- 遷移として、以下の2パターンが存在する
- 9で埋まっていない最小の桁に1を足す(9→19、1099→1199、1999→2999)
- 9で埋まっている範囲のうち一番高い桁に1を足し、繰り上がる(999→1099、19999→20999)
エスパーで解く
とりあえずこれらの観察を証明抜きで全面的に信頼すると、遷移として考えられる2パターンのうち、 が小さいほうを取れば次のすぬけ数が求められそうな気がします…が、この方法は通りません。より上のほうの桁で、99999999999999→100999999999999のような遷移が登場するからです。
(このような遷移を本番中に発見できるかはともかく、)これを考慮して、もう少し遷移の候補を広く考えることにします。「(最上位の0も含めて)どこかの桁に1を足す」を全部探索することにします。
結果的にはこれで、ACが取れます*3。
Submission #2739590 - AtCoder Regular Contest 099
より高速なエスパー
すぬけ数の「差」を取ってみます。
[1, 1, 1, 1, 1, 1, 1, 1, 10, 10, 10, 10, 10, 10, 10, 10, 10, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 100, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 10000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 100000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000, 1000000]
すぬけ数の差を数列としてみると、初項が1で、2番目以降の項は「前の項と同じ数」または「前の項の10倍」になっていることが分かります。そのため、差を2通り試して が小さいほうを取る、という方法が考えられます。
例えば、8→9の差は1なので、9の次の数の候補としては「+1した10」と「+10した19」を試す、という感じです。これでもACが取れます。
Submission #2739671 - AtCoder Regular Contest 099
ちゃんと証明して解く(未)
ちゃんと証明しようとする場合も、遷移先の候補をいくつかに絞って、それ以外の値をとった場合はすぬけ数にならないことを示すことになりそうです。公式解説PDF*4がそういった方針になっているように見えますが、まだ飲み込めていないです。
解説放送で話されていた方法は上記のエスパーより少し遷移の候補が広いですが、そのぶん証明が楽そうです。
もし可能であれば、「より高速なエスパー」で示したような2つの候補だけを考える方法を、証明(または反証)してみたいです。
さいごに
まずはC問題の問題文を読み落としたのが痛いですね…たらればですが、これを最初に読み落としてなければ10分以内には解けていたと思います。
D問題はとても面白い問題だっただけに、本番で通せなかったのが悔やまれます。計算量が予測できずTLEを恐れてしまったこともあり、「ある程度候補を絞ってからの全探索」よりも「一発で次の値が求まる必勝法」を探そうとしてしまいました。
反省内容の多い回でした。今後に活かさなければと思います。